A buffer solution was made by adding 15.0g of CH3COOH and 20.5gCH3COONa. The buffer is diluted to 1.0L.
Calculate the pH of solution.
Given: pKaofCH3COOH=4.74,log(1312)=0.035
The correct Answer is:A, B, C, D
To calculate the pH of the buffer solution made by adding 15.0 g of acetic acid (CH₃COOH) and 20.5 g of sodium acetate (CH₃COONa), we will follow these steps:
Step 1: Calculate the number of moles of CH₃COOH and CH₃COONa
1. Molecular weight of CH₃COOH (acetic acid):
- C: 12.01 g/mol × 2 = 24.02 g/mol
- H: 1.01 g/mol × 4 = 4.04 g/mol
- O: 16.00 g/mol × 2 = 32.00 g/mol
- Total = 24.02 + 4.04 + 32.00 = 60.06 g/mol
2. Moles of CH₃COOH:
Moles of CH₃COOH=15.0 g60.06 g/mol≈0.2497 moles
3. Molecular weight of CH₃COONa (sodium acetate):
- C: 12.01 g/mol × 2 = 24.02 g/mol
- H: 1.01 g/mol × 3 = 3.03 g/mol
- O: 16.00 g/mol × 2 = 32.00 g/mol
- Na: 22.99 g/mol
- Total = 24.02 + 3.03 + 32.00 + 22.99 = 82.04 g/mol
4. Moles of CH₃COONa:
Moles of CH₃COONa=20.5 g82.04 g/mol≈0.2495 moles
Step 2: Calculate the concentrations of CH₃COOH and CH₃COONa in 1 L solution
Since the buffer solution is diluted to a total volume of 1.0 L:
1. Concentration of CH₃COOH:
(CH₃COOH)=0.2497 moles1.0 L=0.2497 M
2. Concentration of CH₃COONa:
(CH₃COONa)=0.2495 moles1.0 L=0.2495 M
Step 3: Use the Henderson-Hasselbalch equation to calculate pH
The Henderson-Hasselbalch equation is given by:
pH=pKa+log((Salt)(Acid))
Substituting the values:
- Given pKa=4.74
- (Salt)=(CH₃COONa)=0.2495 M
- (Acid)=(CH₃COOH)=0.2497 M
Calculating the ratio:
(Salt)(Acid)=0.24950.2497≈0.9992
Taking the logarithm:
log(0.9992)≈−0.0008(Using log(1+x)≈x for small x)
Now substituting back into the equation:
pH=4.74+(−0.0008)≈4.7392
Final Answer:
The pH of the buffer solution is approximately 4.74.
---
- C: 12.01 g/mol × 2 = 24.02 g/mol
- H: 1.01 g/mol × 4 = 4.04 g/mol
- O: 16.00 g/mol × 2 = 32.00 g/mol
- Total = 24.02 + 4.04 + 32.00 = 60.06 g/mol
Moles of CH₃COOH=15.0 g60.06 g/mol≈0.2497 moles
- C: 12.01 g/mol × 2 = 24.02 g/mol
- H: 1.01 g/mol × 3 = 3.03 g/mol
- O: 16.00 g/mol × 2 = 32.00 g/mol
- Na: 22.99 g/mol
- Total = 24.02 + 3.03 + 32.00 + 22.99 = 82.04 g/mol
Moles of CH₃COONa=20.5 g82.04 g/mol≈0.2495 moles
(CH₃COOH)=0.2497 moles1.0 L=0.2497 M
(CH₃COONa)=0.2495 moles1.0 L=0.2495 M
pH=pKa+log((Salt)(Acid))
- Given pKa=4.74
- (Salt)=(CH₃COONa)=0.2495 M
- (Acid)=(CH₃COOH)=0.2497 M
(Salt)(Acid)=0.24950.2497≈0.9992
log(0.9992)≈−0.0008(Using log(1+x)≈x for small x)
pH=4.74+(−0.0008)≈4.7392
The pH of the buffer solution is approximately 4.74.
Topper's Solved these Questions
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Ex 8.4
39 Videos
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Ex 8.5
6 Videos
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Ex 8.2
27 Videos
- HYDROGEN, WATER AND HYDROGEN PEROXIDEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - HYDROGEN, WATER AND HYDROGEN PEROXIDEEXERCISE - Subjective Archive (Subjective)
3 Videos
- ISOMERISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Assertion-Reasoning Type
1 Videos
Similar Questions
Knowledge Check
pH of 0.005 M calcium acetate (pKa of CH3COOH=4.74) is
A7.04B9.37C9.26D8.37
When a buffer solution of CH3COOH and CH3COONais diluted with water
View Solution0.1M CH3COOH(aq.) Is mixed with 0.1M NaOH(aq.). The pH of solution on mixing will be (Ka of CH3COOH is 1.8×10−5
View SolutionTo a buffer solution of CH3,COOH and CH3,COONa, some HCI is added. Then the reaction involved is
View SolutionA solution contains 0.09HC1,0.09MCHC12COOH, and 0.1MCH3COOH. The pH of this solution is one. Calculate Kafor CHC12COOH. (Given KaCH3COOH=10−5)
View SolutionWhich of following aqueous mixture of CH3COOH and CH3COONa will have maximum buffer capacity?
View SolutionGiven the following cell at 25∘C
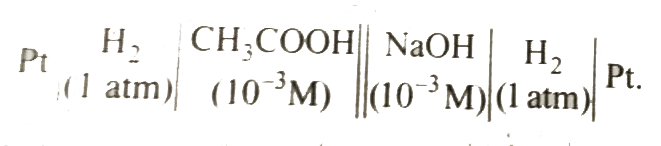
What will be the potential of the cell ?
Given pKa of CH3COOH=4.74
View Solution4 gm NaOH is dissolved in 1 litre solution containing 1 mole CH3COOH and 1 mole CH3COONa. Calculate pH of resulant solution.
(Ka of CH3COOH=1.8×10−5, log11=1.04)
View Solution
