Determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at from theor solubility product constants given in Table . Determine also the molarities of individual ions.
To determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride, and mercurous iodide at 298 K, we will use their solubility product constants (Ksp) provided in the problem statement. We will also calculate the molarities of the individual ions produced upon dissolution.
1. Silver Chromate (Ag2CrO4):
- Dissociation:
Ag2CrO4(s)⇌2Ag+(aq)+CrO2−4(aq)
- Let the solubility be s. Then:
- (Ag+)=2s
- (CrO2−4)=s
- Ksp expression:
Ksp=(Ag+)2(CrO2−4)=(2s)2(s)=4s3
- Given Ksp=1.1×10−12:
4s3=1.1×10−12
s3=1.1×10−124=2.75×10−13
s=(2.75×10−13)1/3≈6.5×10−5M
- Molarities of ions:
- (Ag+)=2s=1.3×10−4M
- (CrO2−4)=s=6.5×10−5M
2. Barium Chromate (BaCrO4):
- Dissociation:
BaCrO4(s)⇌Ba2+(aq)+CrO2−4(aq)
- Let the solubility be s:
- (Ba2+)=s
- (CrO2−4)=s
- Ksp expression:
Ksp=(Ba2+)(CrO2−4)=s2
- Given Ksp=1.2×10−10:
s2=1.2×10−10
s=√1.2×10−10≈1.09×10−5M
- Molarities of ions:
- (Ba2+)=s=1.09×10−5M
- (CrO2−4)=s=1.09×10−5M
3. Ferric Hydroxide (Fe(OH)3):
- Dissociation:
Fe(OH)3(s)⇌Fe3+(aq)+3OH−(aq)
- Let the solubility be s:
- (Fe3+)=s
- (OH−)=3s
- Ksp expression:
Ksp=(Fe3+)(OH−)3=s(3s)3=27s4
- Given Ksp=1.0×10−38:
27s4=1.0×10−38
s4=1.0×10−3827≈3.70×10−40
s=(3.70×10−40)1/4≈1.38×10−10M
- Molarities of ions:
- (Fe3+)=s=1.38×10−10M
- (OH−)=3s=4.14×10−10M
4. Lead Chloride (PbCl2):
- Dissociation:
PbCl2(s)⇌Pb2+(aq)+2Cl−(aq)
- Let the solubility be s:
- (Pb2+)=s
- (Cl−)=2s
- Ksp expression:
Ksp=(Pb2+)(Cl−)2=s(2s)2=4s3
- Given Ksp=1.6×10−5:
4s3=1.6×10−5
s3=1.6×10−54=4.0×10−6
s=(4.0×10−6)1/3≈0.0159M
- Molarities of ions:
- (Pb2+)=s=0.0159M
- (Cl−)=2s=0.0318M
5. Mercurous Iodide (Hg2I2):
- Dissociation:
Hg2I2(s)⇌2Hg+(aq)+2I−(aq)
- Let the solubility be s:
- (Hg+)=2s
- (I−)=2s
- Ksp expression:
Ksp=(Hg+)2(I−)2=(2s)2(2s)2=16s4
- Given Ksp=4.5×10−29:
16s4=4.5×10−29
s4=4.5×10−2916≈2.8125×10−30
s=(2.8125×10−30)1/4≈4.09×10−8M
- Molarities of ions:
- (Hg+)=2s=8.18×10−8M
- (I−)=2s=8.18×10−8M
Summary of Results:
- Silver Chromate:
- Solubility: 6.5×10−5M
- (Ag+)=1.3×10−4M, (CrO2−4)=6.5×10−5M
- Barium Chromate:
- Solubility: 1.09×10−5M
- (Ba2+)=1.09×10−5M, (CrO2−4)=1.09×10−5M
- Ferric Hydroxide:
- Solubility: 1.38×10−10M
- (Fe3+)=1.38×10−10M, (OH−)=4.14×10−10M
- Lead Chloride:
- Solubility: 0.0159M
- (Pb2+)=0.0159M, (Cl−)=0.0318M
- Mercurous Iodide:
- Solubility: 4.09×10−8M
- (Hg+)=8.18×10−8M, (I−)=8.18×10−8M
- Dissociation:
Ag2CrO4(s)⇌2Ag+(aq)+CrO2−4(aq)
- Let the solubility be s. Then:
- (Ag+)=2s
- (CrO2−4)=s
- Ksp expression:
Ksp=(Ag+)2(CrO2−4)=(2s)2(s)=4s3
- Given Ksp=1.1×10−12:
4s3=1.1×10−12
s3=1.1×10−124=2.75×10−13
s=(2.75×10−13)1/3≈6.5×10−5M
- Molarities of ions:
- (Ag+)=2s=1.3×10−4M
- (CrO2−4)=s=6.5×10−5M
- Dissociation:
BaCrO4(s)⇌Ba2+(aq)+CrO2−4(aq)
- Let the solubility be s:
- (Ba2+)=s
- (CrO2−4)=s
- Ksp expression:
Ksp=(Ba2+)(CrO2−4)=s2
- Given Ksp=1.2×10−10:
s2=1.2×10−10
s=√1.2×10−10≈1.09×10−5M
- Molarities of ions:
- (Ba2+)=s=1.09×10−5M
- (CrO2−4)=s=1.09×10−5M
- Dissociation:
Fe(OH)3(s)⇌Fe3+(aq)+3OH−(aq)
- Let the solubility be s:
- (Fe3+)=s
- (OH−)=3s
- Ksp expression:
Ksp=(Fe3+)(OH−)3=s(3s)3=27s4
- Given Ksp=1.0×10−38:
27s4=1.0×10−38
s4=1.0×10−3827≈3.70×10−40
s=(3.70×10−40)1/4≈1.38×10−10M
- Molarities of ions:
- (Fe3+)=s=1.38×10−10M
- (OH−)=3s=4.14×10−10M
- Dissociation:
PbCl2(s)⇌Pb2+(aq)+2Cl−(aq)
- Let the solubility be s:
- (Pb2+)=s
- (Cl−)=2s
- Ksp expression:
Ksp=(Pb2+)(Cl−)2=s(2s)2=4s3
- Given Ksp=1.6×10−5:
4s3=1.6×10−5
s3=1.6×10−54=4.0×10−6
s=(4.0×10−6)1/3≈0.0159M
- Molarities of ions:
- (Pb2+)=s=0.0159M
- (Cl−)=2s=0.0318M
- Dissociation:
Hg2I2(s)⇌2Hg+(aq)+2I−(aq)
- Let the solubility be s:
- (Hg+)=2s
- (I−)=2s
- Ksp expression:
Ksp=(Hg+)2(I−)2=(2s)2(2s)2=16s4
- Given Ksp=4.5×10−29:
16s4=4.5×10−29
s4=4.5×10−2916≈2.8125×10−30
s=(2.8125×10−30)1/4≈4.09×10−8M
- Molarities of ions:
- (Hg+)=2s=8.18×10−8M
- (I−)=2s=8.18×10−8M
- Silver Chromate:
- Solubility: 6.5×10−5M
- (Ag+)=1.3×10−4M, (CrO2−4)=6.5×10−5M
- Barium Chromate:
- Solubility: 1.09×10−5M
- (Ba2+)=1.09×10−5M, (CrO2−4)=1.09×10−5M
- Ferric Hydroxide:
- Solubility: 1.38×10−10M
- (Fe3+)=1.38×10−10M, (OH−)=4.14×10−10M
- Lead Chloride:
- Solubility: 0.0159M
- (Pb2+)=0.0159M, (Cl−)=0.0318M
- Mercurous Iodide:
- Solubility: 4.09×10−8M
- (Hg+)=8.18×10−8M, (I−)=8.18×10−8M
Topper's Solved these Questions
- NCERT BASED EXERCISEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - Thermodynamics
50 Videos
- ISOMERISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Assertion-Reasoning Type
1 Videos
- ORGANIC REACTION MECHANISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ORGANIC REACTION MECHANISMEXERCISE - Analytical and Descriptive
6 Videos
Similar Questions
Determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at 298 K form their solubility product constants given below. Determine also the molarities of individual ions.
KSP(Ag2CrO4)=1.1×10−12,
KSP(BaCrO4)=1.2×10−10,
KSP[Fe(OH)3]=1.0×10−38,
KSP(PbCI2)=1.6×10−5,
KSP(Hg2I2)=4.5×10−29.
View SolutionDetermine the solubility of silver chromate at 298 K given its Ksp value is 1.1×10−12?
View Solution(a) Apply Kohlrausch law of independent migration of ions, write the expression to determine the limiting molar conductivity of calcium chloride.
(b) Given are the conductivity and molar conductivity of NaCI solutions at 298 K at different concentrations :
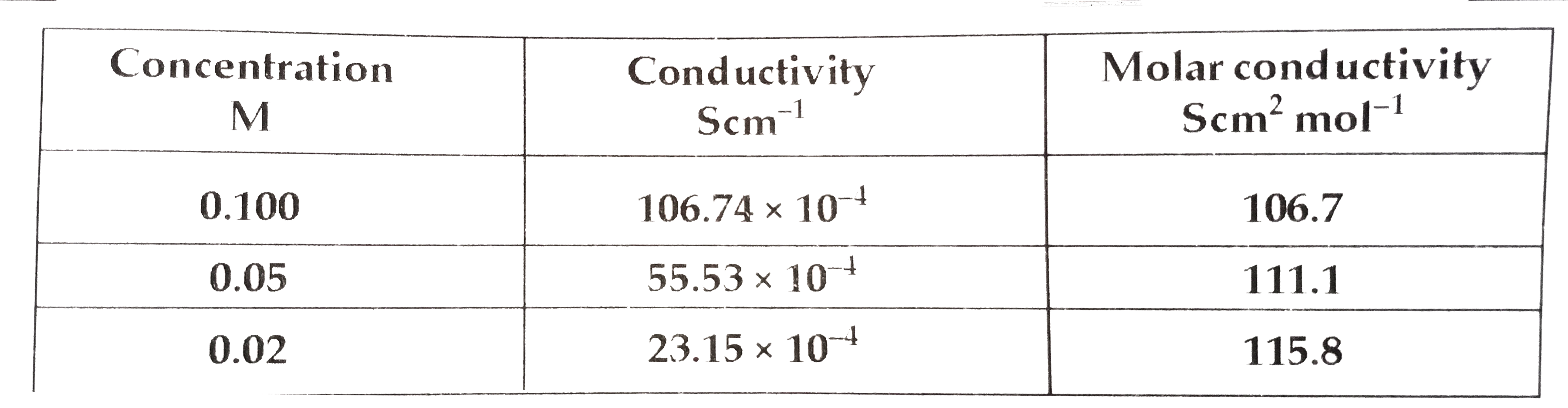
Compare the variation of conductivity and molar conductivity of NaCI solutions on dilution. Give reason.
(c) 0.1 M KCI solution offered a resistance of 100 ohms in conductivity cell at 298 K. If the cell constant of the cell is 1.29cm−1, calculate the molar conductivity of KCI solution.
View SolutionA solution which remains in equilibrium with undissolved solute , in contact , is said to be saturated . The concentration of a saturated solution at a given temperature is a called solubility . The product of concentration of ions in a saturated solution of an electrolyte at a given temperature is called solubility product (Ksp) . For the electrolyte Ax,By with solubility S.
The solubility product (Ksp) is given as Ksp=xx×yy×Sx−y . While calculating the solubility of a sparingly . soluable salt in the presence of some strong electrolyte containing a common ion , the common ion concentration is practically equal to that of strong electrolyte containing a common ion . the common ion soncentration is practically equal to that of strong electrolyte . If in a solution , the ionic product of an electroylte exceeds its Ksp value at a particular temperature , then precipitation occurs . If two or more electrolyte are presentt in the solution , then by the addition of some suitable reagent , precipitation generally occurs in increasing order of their ksp values . Solubility of some sparingly soluable salts , is sometimes enhanced through complexation . While we are calculating the solubility of some sparingly or pH of an electrolyte , the nature of cation of anion should be checked carefully whether there ion (s) are capable of undergoing hydrolysis or not . If either or both of the ions are capable of undergoing hydrolysis , it should be taken into account in calculating the solubility . While calculating the pH of an amphiprotic species , it should be checked whether or not cation can undergo hydrolysis . Total aH−=√Ka1×Ka2 (if cation do not undergo hydrolysis )
aH+=√Ka1(KwKb−Ka2) (if cation also undergoes hydrolysis ) where symbols have usual meaning . Solubility of solids into liquids is a function of temperature alone but solubility of gases into liquids is a function of temperature as well as pressure . The effect of pressure on solubility of gases into liquids is governed by Henry's law .
The solubility of BaSO4 in 0.1 M BaCl2 solution is (Ksp of BaSO4=1.5×10−9)
View SolutionDetermine the molar solubility of MgF2 from its solubility product Ksp=4×10−9 :
View SolutionConsider a sturated solution of silver chloride that is in contact with solid silver chloride. The solubility equilibrium can be represented as
AgCl(s)⇔Ag+(aq.)+Cl−(aq.), Ksp=[Ag+(aq.)][Cl−(aq.)]
Where Ksp is clled the solubility product constant or simply the solubility product. In general, the solubility product of a compound is the product of the molar concentrations of the constituent ions, each raised to the power of its stoichiometric coefficient in the equilibrium equation.
For concentrations of ions that do not necessarliy correpond to equilibrium conditions we use the reaction quotient (Q) which is clled the ion or ionic prodect (Q) to predict whether a precipitate will from. Note that (Q) has the same for as Ksp are
Q<Ksp Unsaturated solution
Q=Ksp Saturated solution
Q>sp Supersaturated solution, precipitate will from
The soluvility molar solubility of ferric hydroxide in aqueous solution is 6×10−38 at 298 K. the solubility of Fe3+ ion will increase when the :
View SolutionConsider a sturated solution of silver chloride that is in contact with solid silver chloride. The solubility equilibrium can be represented as
AgCl(s)⇔Ag+(aq.)+Cl−(aq.), Ksp=[Ag+(aq.)][Cl−(aq.)]
Where Ksp is clled the solubility product constant or simply the solubility product. In general, the solubility product of a compound is the product of the molar concentrations of the constituent ions, each raised to the power of its stoichiometric coefficient in the equilibrium equation.
For concentrations of ions that do not necessarliy correpond to equilibrium conditions we use the reaction quotient (Q) which is clled the ion or ionic prodect (Q) to predict whether a precipitate will from. Note that (Q) has the same for as Ksp are
Q<Ksp Unsaturated solution
Q=Ksp Saturated solution
Q>sp Supersaturated solution, precipitate will from
Will a precipitate from if 1 volume of 0.1 volume of 0.1 MPb2+ ion solution in mixed with 3 volume of 0.3 M Cl− ion solution ? [Givem:Ksp(PbCl2)=1.7×10−5M3]
View SolutionConsider a sturated solution of silver chloride that is in contact with solid silver chloride. The solubility equilibrium can be represented as
AgCl(s)⇔Ag+(aq.)+Cl−(aq.), Ksp=[Ag+(aq.)][Cl−(aq.)]
Where Ksp is clled the solubility product constant or simply the solubility product. In general, the solubility product of a compound is the product of the molar concentrations of the constituent ions, each raised to the power of its stoichiometric coefficient in the equilibrium equation.
For concentrations of ions that do not necessarliy correpond to equilibrium conditions we use the reaction quotient (Q) which is clled the ion or ionic prodect (Q) to predict whether a precipitate will from. Note that (Q) has the same for as Ksp are
Q<Ksp Unsaturated solution
Q=Ksp Saturated solution
Q>sp Supersaturated solution, precipitate will from
At 25∘C, will a precipitate of Mg (OH)2 from when a 0.0001 M solution of Mg(NO3)2 is adjusted to a pH of 9.0 ? At what minimum value of pH will precipition start ?
[Given:Ksp(Mg(OH)2)=10−11M3]
View SolutionConsider a sturated solution of silver chloride that is in contact with solid silver chloride. The solubility equilibrium can be represented as
AgCl(s)⇔Ag+(aq.)+Cl−(aq.), Ksp=[Ag+(aq.)][Cl−(aq.)]
Where Ksp is clled the solubility product constant or simply the solubility product. In general, the solubility product of a compound is the product of the molar concentrations of the constituent ions, each raised to the power of its stoichiometric coefficient in the equilibrium equation.
For concentrations of ions that do not necessarliy correpond to equilibrium conditions we use the reaction quotient (Q) which is clled the ion or ionic prodect (Q) to predict whether a precipitate will from. Note that (Q) has the same for as Ksp are
Q<Ksp Unsaturated solution
Q=Ksp Saturated solution
Q>sp Supersaturated solution, precipitate will from
Will a precipitate from if 50 cm3 of 0.01 M AgNO3 and 50 cm3 of 2×10−5 M NaCl are mixed?
[Given:Ksp(AgCl)=10−10M2]
View SolutionA one litre solution is prepared by dissolving some lead-nitrate in water. The solution was found to boil at 100.15∘C. To the resulting solution 0.2 mole NaCI was added. The resulting solution was found to freeze at 0.83∘C. Determine solubility product of PbCI2. Given Kb=0.5 and Kf=1.86. Assume molality to be equal to molarity in all case.
View Solution
