A sample of a crystalline solid scatters a beam of X-rays of wavelength 70.93 pm at an angle 2θ of 14.66∘. If this is a second-order reflection (n=2), calculate the distance between the parallel planers of atoms from which the scattered beam appears to have been reflected.
To solve the problem, we will use Bragg's Law, which is given by the equation:
nλ=2dsinθ
where:
- n is the order of reflection,
- λ is the wavelength of the X-rays,
- d is the distance between the planes of atoms,
- θ is the angle of incidence (half of 2θ).
Step 1: Write down the given data
- Wavelength λ=70.93 pm
- Angle 2θ=14.66∘
- Order of reflection n=2
Step 2: Convert the wavelength from picometers to meters
1 picometer (pm) = 10−12 meters
λ=70.93pm=70.93×10−12m
Step 3: Calculate θ
Since 2θ=14.66∘, we can find θ by dividing by 2:
θ=14.66∘2=7.33∘
Step 4: Calculate sinθ
Using a calculator or trigonometric tables, we find:
sin(7.33∘)≈0.1275
Step 5: Substitute values into Bragg's Law
Now we can substitute the values into the equation nλ=2dsinθ:
2×70.93×10−12=2d×0.1275
Step 6: Simplify the equation
We can cancel the 2 on both sides:
70.93×10−12=d×0.1275
Step 7: Solve for d
Now, isolate d:
d=70.93×10−120.1275
Calculating this gives:
d≈555.3×10−12m
Step 8: Final answer
Converting to a more standard form:
d≈556.3pm
Summary
The distance between the parallel planes of atoms is approximately 556.3pm.
---
- n is the order of reflection,
- λ is the wavelength of the X-rays,
- d is the distance between the planes of atoms,
- θ is the angle of incidence (half of 2θ).
- Wavelength λ=70.93 pm
- Angle 2θ=14.66∘
- Order of reflection n=2
1 picometer (pm) = 10−12 meters
Since 2θ=14.66∘, we can find θ by dividing by 2:
Using a calculator or trigonometric tables, we find:
Now we can substitute the values into the equation nλ=2dsinθ:
We can cancel the 2 on both sides:
Now, isolate d:
Converting to a more standard form:
The distance between the parallel planes of atoms is approximately 556.3pm.
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Solved Examples
13 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)
13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
4 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
An X-ray beam (λ=70.9pm) was scattered by a crystalline solid. The angle (2θ) of the diffraction for a second order reflection is 14.660. Calculate the distance between parallel planes of atoms of the crystalline solid.
View SolutionThe second order Bragg diffraction of X-rays with λ=1.0Å from a set of parallel planes in a metal occurs at an angle 60∘. The distance between the scattering planes in the crystals is
View Solution
Knowledge Check
A parallel beam of light of wavelength 600 nm is incident normally on a slit of width d. If the distance between the slits and the screen is 0.8 m and the distance of 2nd order maximum from the centre of the screen is 15 mm. The width of the slit is
A40μmB80μmC160μmD200μm
Calculate λ of X-rays which give a diffraction angle 2θ=16.8∘ for crystal, if the interplanar distance in the crystal is 0.2nm and that only for the first-order diffraction is observed. Given sin8.40∘=0.146.
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
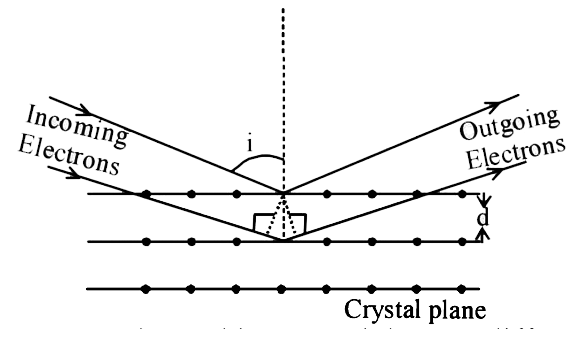
If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)
View SolutionAnswer the following:
(a) What is a wave front? How does it propagate? Using Huygens' principle, explain reflection of a plane wavefront from a surface and verify the laws of reflection.
(b) A parallel beam of light of wavelength 500nm falls on a narrow slit and the resulting diffraction pattern is obtained on a screen 1m away. If the first minimum is formed at a distance of 2.5mm from the centre of screen, find the
(i) width of the slit, and
(ii) distance of first secondary maximum from the centre of the screen.
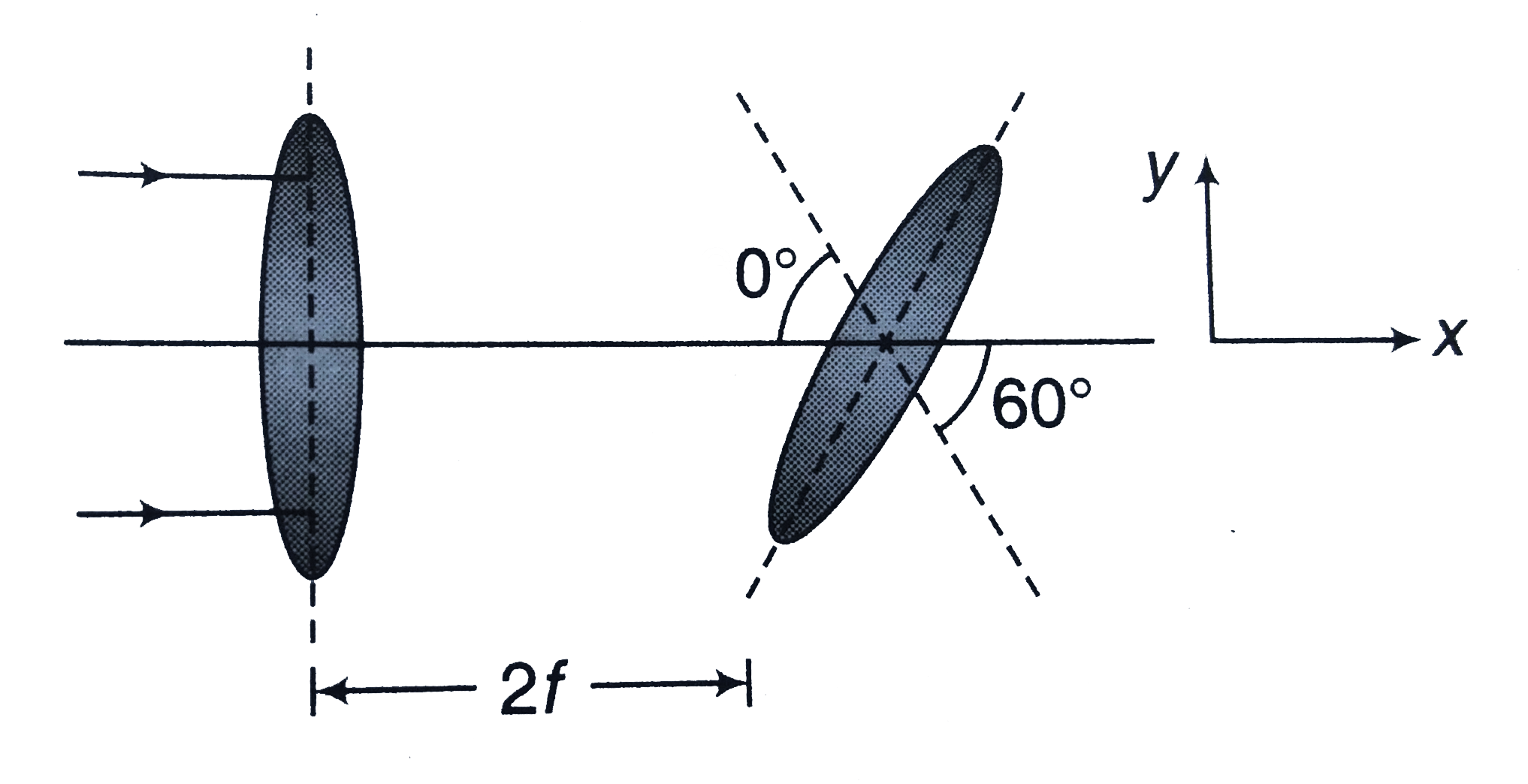
View SolutionTwo converging lenses of the same focal length f are separated by a distance 2f. The axis of the second lens is inclined at angle θ=60∘ with respect to the axis of the first lens. A parallel paraxial beam of light is incident from left side of the lens. Find the coordinates of the final image with respect to the origin of the first lens.
View SolutionX-rays of wavelength 22 pm are scattered from a carbon target at an angle of 85∘ to the incident beam The Compton shift for X-rays is (cos85∘=0.088)
View SolutionCsBr crystallizes in a body-centred cubic unit lattice with an edge length of 4.287Å. Calculate the angles at which the second-order reflection maxima may be expected for (2,0,0), (1,1,0), planes when X-rays of γ=0.50Å are used.
View SolutionA parallel beam of rays is incident on a consisting pf three thin lenses with a common optical axis. The focal length of the lenses are equal to f1=+10cmandf2=−20cm,andf3=+9cm respectively. The distance between the first and the second lens is 15cm and between the second and the third is 5cm. Find the position of the point at which the beam converges when it leaves the system of lenses.
View Solution
