A compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body centre and at the edge centre of the cube.
a. Celculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
b. If all the atoms are removed from one of the body diagonals of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
c. If all the atoms from the diagonals of the one of the face of the cube are removed, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
d. If all the atoms are removed from one of the plane passing through the middle of t he cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
e. If all the atoms are removed from one of the axes passing through one of the face centres of the cube, calculate (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
a. Zeff(X)=nc8+nf2=88+62=1+3=4
Zeff(Y)=nb8+ne4=11+124=1+3=4.
Zeff(X+Y)=4+4=8
ii. Total number of atoms in the cube
ii. =8 (corners) +6(face centre)+1 (body centre)
+12 (edge centre)
=27 atoms/units cube
(iii). Formula: Zeff(X)=4,Zeff(Y)=4
implies X4Y4=4XY
b. i.
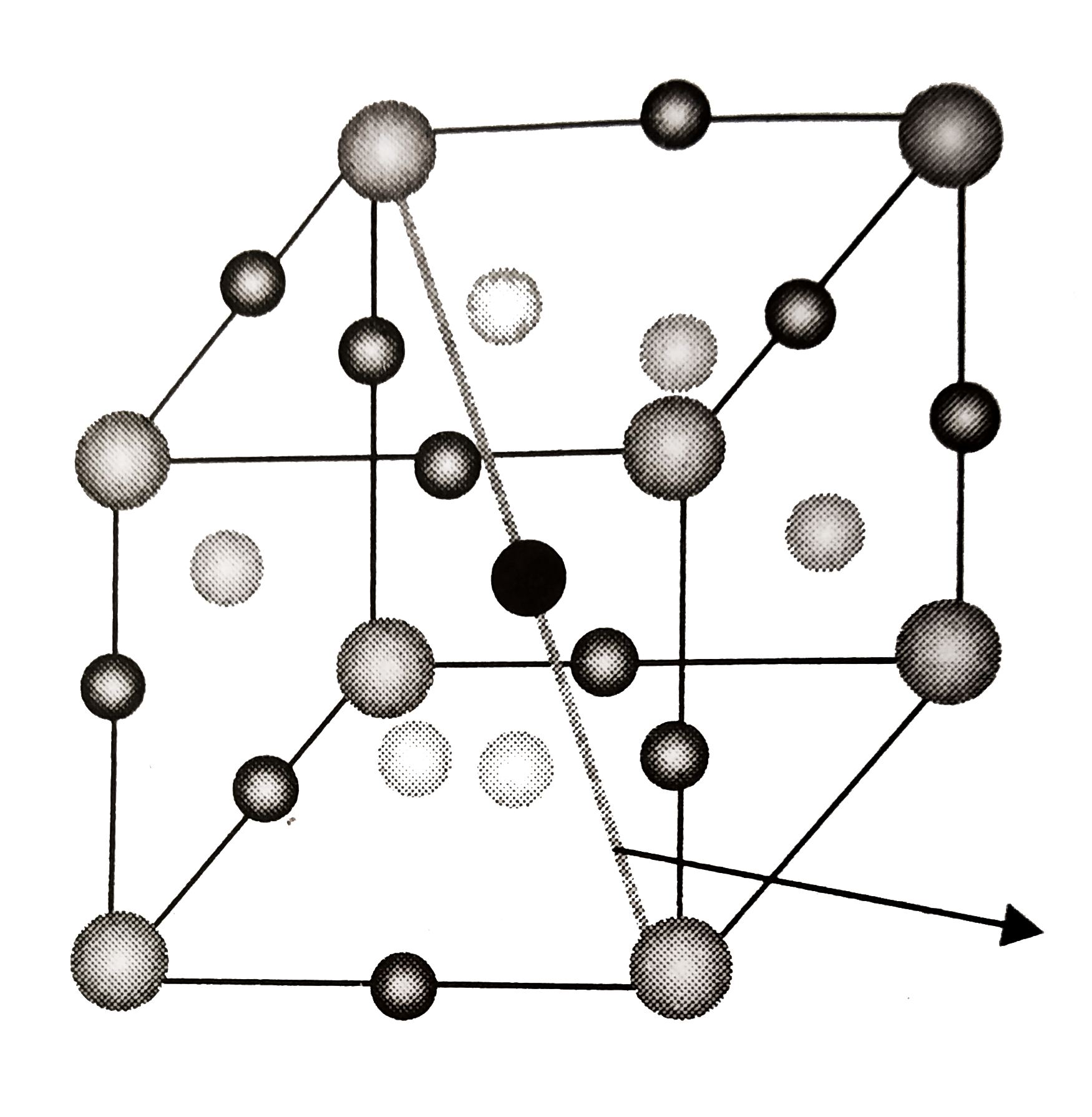
Atoms removed from one body diagonal
=2 atom form corner +1 atom form body centre
=3 atoms. Zeff(X)=nc8+nf2=8−28+62=154
Zeff(Y)=nb8+nc4=1−11+124=0+3=3
Zeff(X+Y)=154+3=274
ii. Total number of atoms in the cube
=6(corner)+6(face centre)+ Zero (body centre) +12 (edge centres)
=24 atoms/unit cube
iii. Zeff(X)=154,Zeff(Y)=3
⇒X(154)Y3.
Simplifying X15Y12
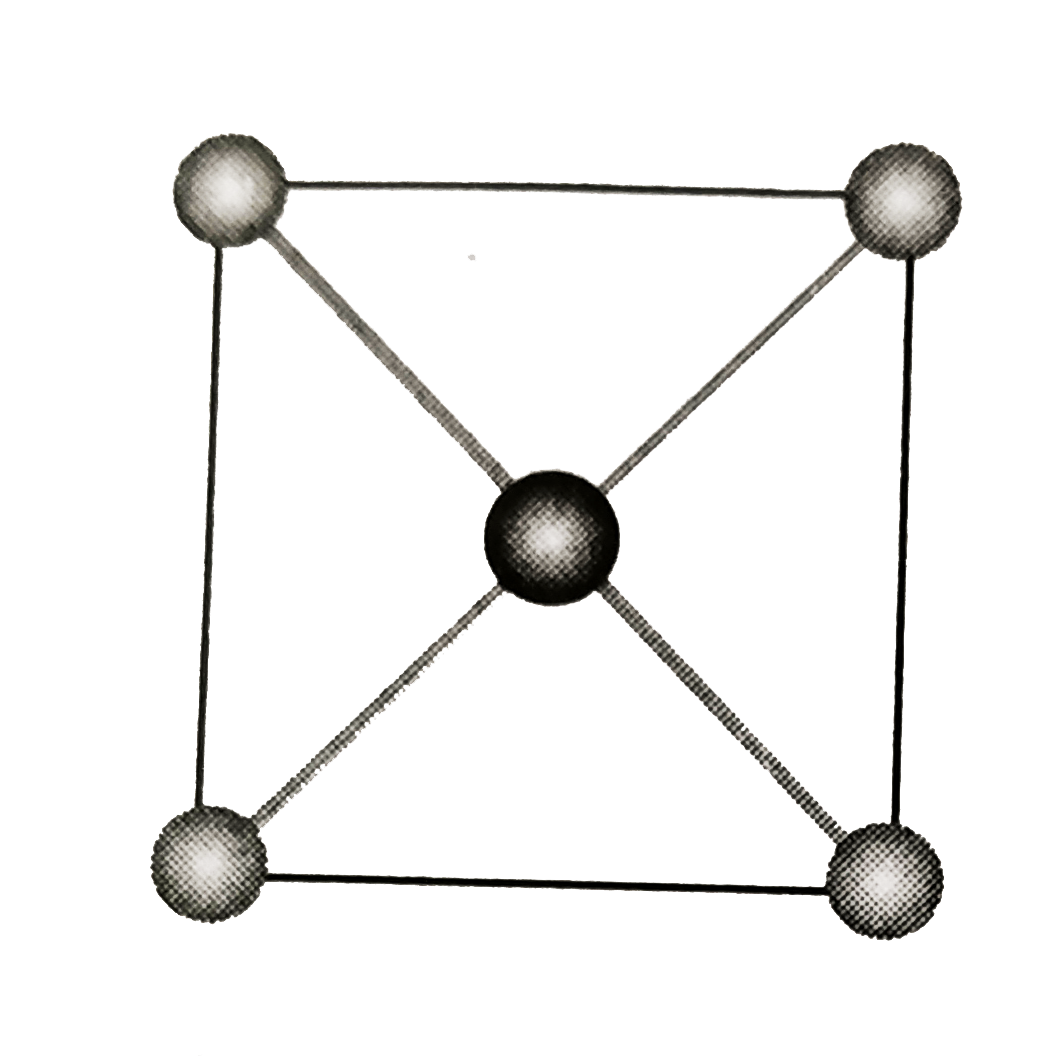
Zeff(X)=nc8+nf2=8−48+6−12=1+2=3.
Zeff(Y)=nb8+nc4=1−11+124=1+3=4
Zeff(X)=3+4=7
ii. Total number of atoms in a cube
=4(corner)+5(face centre)+1 (body centre)
+12 (edge centre)
=22 atoms/unit cube
iii. Formula: Zeff(X)=3,Zeff(Y)=4
⇒X3Y4.
d. Plane passing through the middle of cube (other atoms are not shown)
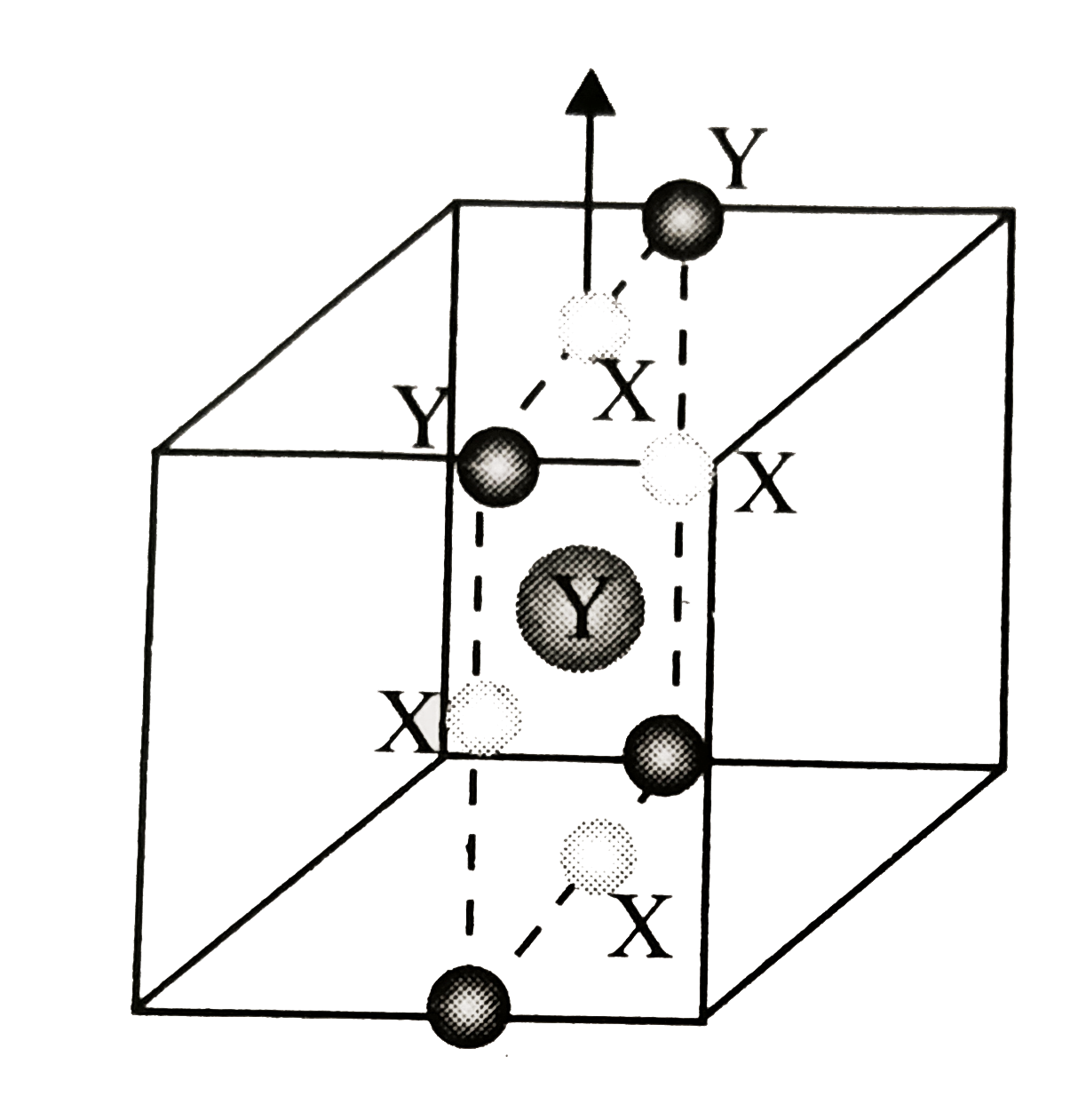
i. Zeff(X)=nc8+nf2=88+6−42=1+1=2
Zeff(Y)=nb8+nc4=(1−1)1+(12−4)4=2.
Zeff(X+Y)=2+2=4
ii. Total number of the atoms in the cube
=8(corner)+2(face centres)+ zero (body centre) +8 (edge centres)
=18 atoms/unit cube
iii. Formula: Zeff(X)=2,Zeff(Y)=2
e. 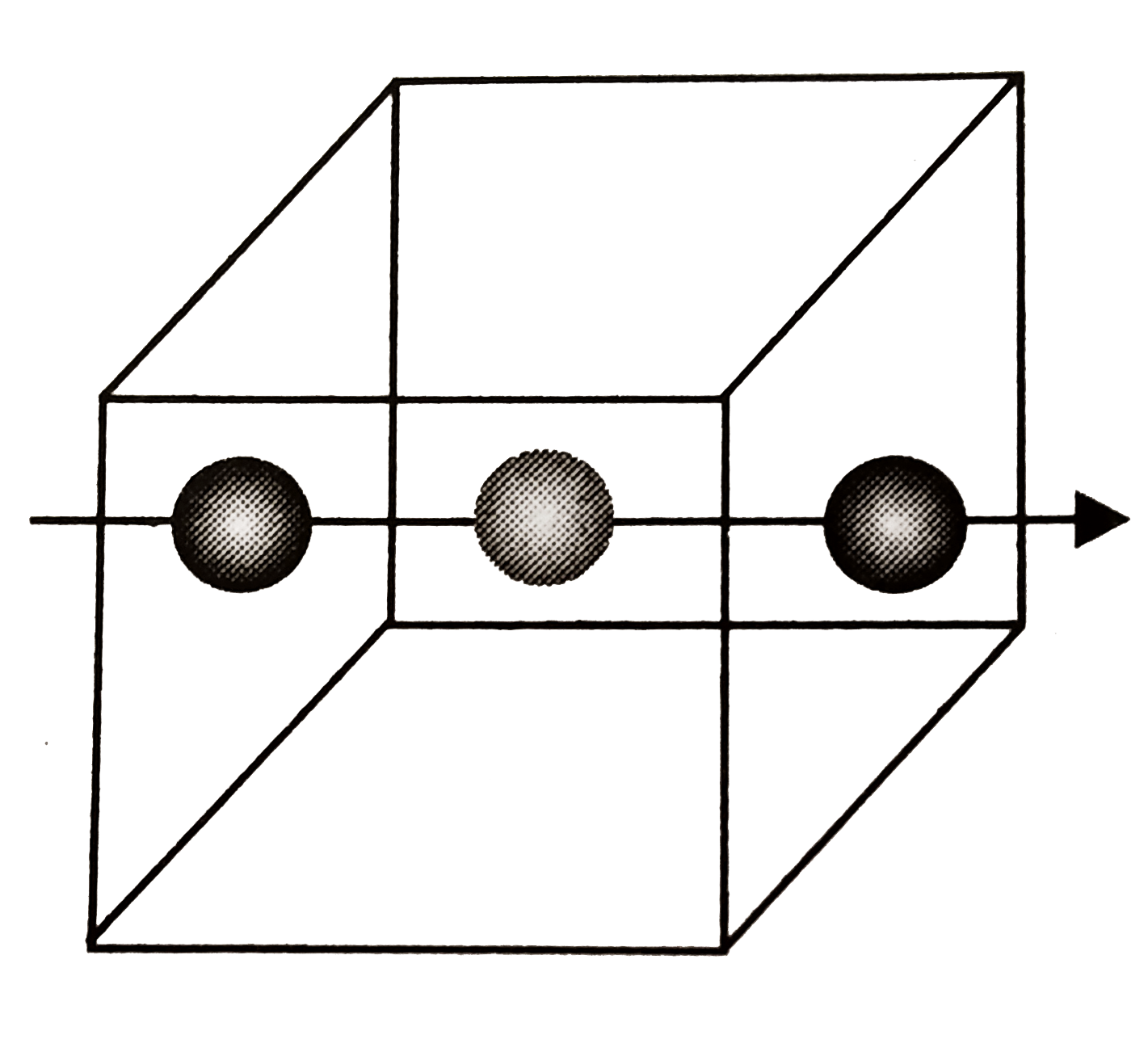
Zeff(X)=nc8+nf2=88+(6−2)2=1+2=3
Zeff(Y)=nb8+nc4=(1−1)1+124=0+3=3.
Zeff(X+Y)=3+3=6.
ii. Total number atom in a cube =8 (corner) +6 (face centre)
zero (body centre) +12 (edge centre)
=24 atoms/unit cube
iii. Formula: Zeff(X)=3,Zeff(Y)=3
Formula is X3Y3 or 3XY.
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Solved Examples
13 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)
13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
4 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
A compound formed by elements X and Y has a cubic structure in which X atoms are at the corner of the cube and Y atoms are at the face centres. One atoms X is misssing from the corner.
a. Calculate (i). Zeff' (ii). total number of the atoms in the cube, and (iii). formula of the compound.
b. If alll the atoms are removed from one of the faces of the cube containing atoms at corners, as in (a) above, calculate (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
View SolutionA compound formed by elements A and B has a cubic structure in which A atoms are at the corner of the cube and B atoms are at the face centres. Derive the fomula of the compound.
View Solution
Knowledge Check
A compound formed by elements A and B has a cubic structure in which A atoms are at the corners of cube and B atoms are at the face centres. The formula of the compound will be:
AA2B4BAB3CAB5DA2B6
A compound formed by elements X and Y has a cubic structure in which X atoms are at the corners of the cube of and two atoms (Y) are at each body diagonal of the cube.
a. Calculate: (i) Zeff' (ii) total number of atoms in a cube, and (iii) formula of the compound.
b. If all atoms form one body diagonal of the cube except corners are removed, calculate: (i) Zeff' (ii) total number of atoms in the cube, and (iii) formula of the compound.
View SolutionA compound formed by elements X, Y and Z has a cubic structure in which X atoms are at the corner of the cube and also at alternate face centres. Y atoms are present at the body centre and Z atoms are present at the alternate edge centre. Then the molecular formula of the compound is
View SolutionA compound formed by elements X and Y crystallises in a cubic structure in which the X atoms are at the alternate corners of a cube and the Y atoms are at the face centres.The formula of the compound is
View SolutionA compound formed by elements A and B crystallizes in cubic structure where A atoms are at the corners of a cube and B atoms are at the face center . What is the formula of the compound ?
View SolutionA solid has a cubic structure in which X atoms are located at the corners of the cube, Y atoms are at the cube centres and O atoms are at the edge centres. What is the formula of the compound?
View SolutionA compound formed by elements A and B crystallizes in the cubic arrangement in which atoms A are at the corners of the cube and atoms B at the face centres. What is the formula of the compound?
View SolutionA compound formed by element X and Y crystallizes in the cubic structure when Y atoms are at the corners of the cube and X atoms are at the alternate faces. What is the formula of the compound?
View Solution
