Calculate the miller indices of crystal. Planes which cut through the crystal axes at
(2a,3b,c)
(a,b,c)
(6a,3b,3c)
(2a,−3b,−3c)
To calculate the Miller indices for the given crystal planes, we will follow a systematic approach for each point provided. The points given are:
1. (2a, 3b, c)
2. (a, b, c)
3. (6a, 3b, 3c)
4. (2a, -3b, -3c)
Step 1: Calculate Miller Indices for (2a, 3b, c)
1. Identify Intercepts:
- The intercepts are:
- x-axis: 2 (for 2a)
- y-axis: 3 (for 3b)
- z-axis: 1 (for c, since c = 1c)
2. Reciprocate the Intercepts:
- The reciprocals are:
- x-axis: 1/2
- y-axis: 1/3
- z-axis: 1/1
3. Clear the Fractions:
- The least common multiple (LCM) of the denominators (2, 3, 1) is 6.
- Multiply each reciprocal by 6:
- x-axis: 6 * (1/2) = 3
- y-axis: 6 * (1/3) = 2
- z-axis: 6 * (1/1) = 6
4. Miller Indices:
- The Miller indices for (2a, 3b, c) are (3, 2, 6).
Step 2: Calculate Miller Indices for (a, b, c)
1. Identify Intercepts:
- The intercepts are:
- x-axis: 1 (for a)
- y-axis: 1 (for b)
- z-axis: 1 (for c)
2. Reciprocate the Intercepts:
- The reciprocals are:
- x-axis: 1/1
- y-axis: 1/1
- z-axis: 1/1
3. Clear the Fractions:
- No fractions to clear, the values remain:
- x-axis: 1
- y-axis: 1
- z-axis: 1
4. Miller Indices:
- The Miller indices for (a, b, c) are (1, 1, 1).
Step 3: Calculate Miller Indices for (6a, 3b, 3c)
1. Identify Intercepts:
- The intercepts are:
- x-axis: 6 (for 6a)
- y-axis: 3 (for 3b)
- z-axis: 3 (for 3c)
2. Reciprocate the Intercepts:
- The reciprocals are:
- x-axis: 1/6
- y-axis: 1/3
- z-axis: 1/3
3. Clear the Fractions:
- The LCM of (6, 3, 3) is 6.
- Multiply each reciprocal by 6:
- x-axis: 6 * (1/6) = 1
- y-axis: 6 * (1/3) = 2
- z-axis: 6 * (1/3) = 2
4. Miller Indices:
- The Miller indices for (6a, 3b, 3c) are (1, 2, 2).
Step 4: Calculate Miller Indices for (2a, -3b, -3c)
1. Identify Intercepts:
- The intercepts are:
- x-axis: 2 (for 2a)
- y-axis: -3 (for -3b)
- z-axis: -3 (for -3c)
2. Reciprocate the Intercepts:
- The reciprocals are:
- x-axis: 1/2
- y-axis: -1/3
- z-axis: -1/3
3. Clear the Fractions:
- The LCM of (2, 3, 3) is 6.
- Multiply each reciprocal by 6:
- x-axis: 6 * (1/2) = 3
- y-axis: 6 * (-1/3) = -2
- z-axis: 6 * (-1/3) = -2
4. Miller Indices:
- The Miller indices for (2a, -3b, -3c) are (3, -2, -2), which can be represented as (3, 2̅, 2̅).
Final Miller Indices:
1. (2a, 3b, c) → (3, 2, 6)
2. (a, b, c) → (1, 1, 1)
3. (6a, 3b, 3c) → (1, 2, 2)
4. (2a, -3b, -3c) → (3, 2̅, 2̅)
2. (a, b, c)
3. (6a, 3b, 3c)
4. (2a, -3b, -3c)
- The intercepts are:
- x-axis: 2 (for 2a)
- y-axis: 3 (for 3b)
- z-axis: 1 (for c, since c = 1c)
- The reciprocals are:
- x-axis: 1/2
- y-axis: 1/3
- z-axis: 1/1
- The least common multiple (LCM) of the denominators (2, 3, 1) is 6.
- Multiply each reciprocal by 6:
- x-axis: 6 * (1/2) = 3
- y-axis: 6 * (1/3) = 2
- z-axis: 6 * (1/1) = 6
- The Miller indices for (2a, 3b, c) are (3, 2, 6).
- The intercepts are:
- x-axis: 1 (for a)
- y-axis: 1 (for b)
- z-axis: 1 (for c)
- The reciprocals are:
- x-axis: 1/1
- y-axis: 1/1
- z-axis: 1/1
- No fractions to clear, the values remain:
- x-axis: 1
- y-axis: 1
- z-axis: 1
- The Miller indices for (a, b, c) are (1, 1, 1).
- The intercepts are:
- x-axis: 6 (for 6a)
- y-axis: 3 (for 3b)
- z-axis: 3 (for 3c)
- The reciprocals are:
- x-axis: 1/6
- y-axis: 1/3
- z-axis: 1/3
- The LCM of (6, 3, 3) is 6.
- Multiply each reciprocal by 6:
- x-axis: 6 * (1/6) = 1
- y-axis: 6 * (1/3) = 2
- z-axis: 6 * (1/3) = 2
- The Miller indices for (6a, 3b, 3c) are (1, 2, 2).
- The intercepts are:
- x-axis: 2 (for 2a)
- y-axis: -3 (for -3b)
- z-axis: -3 (for -3c)
- The reciprocals are:
- x-axis: 1/2
- y-axis: -1/3
- z-axis: -1/3
- The LCM of (2, 3, 3) is 6.
- Multiply each reciprocal by 6:
- x-axis: 6 * (1/2) = 3
- y-axis: 6 * (-1/3) = -2
- z-axis: 6 * (-1/3) = -2
- The Miller indices for (2a, -3b, -3c) are (3, -2, -2), which can be represented as (3, 2̅, 2̅).
2. (a, b, c) → (1, 1, 1)
3. (6a, 3b, 3c) → (1, 2, 2)
4. (2a, -3b, -3c) → (3, 2̅, 2̅)
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Solved Examples
13 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)
13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
4 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
The Miller indices of a plane having intercepts 2a,2b,∞are
View SolutionA calcite crystal placed over an ink dot is rotated. On seeing through the crystal one finds
View SolutionFind the equation of the plane which cuts intercepts 2,3,-4 on the axes.
View SolutionCalculate the percentage mass of water in crystals of washing soda.
View SolutionWhich has hcp crystal structure ?
View SolutionWhich has hcp crystal structure ?
View SolutionA metal crystallizes into two cubic phases BCC and FCC. The ratio of densities of FCC and BCC is equal to 1.5. Calculate the difference between the unit cell lengths of the FCC and BCC crystals if the edge length of the FCC crystal is equal to 4.0 Å.
View SolutionGive the scientific name of soil bacterium which produces crystal (Cry) proteins.
View SolutionWhen CO2 is passed through brine solution , saturated with ammonia, white crystals precipitate out these crystals are of
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
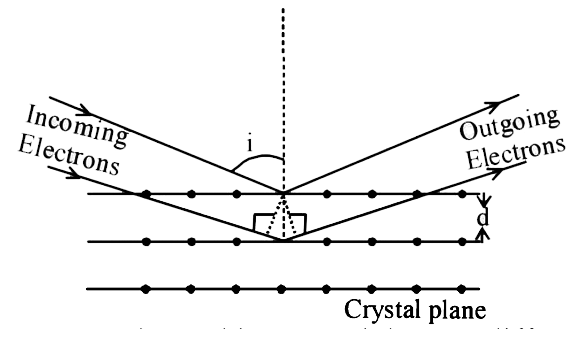
If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)
View Solution