AX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣
∣
∣
∣
∣
∣
∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣
∣
∣
∣
∣
∣
∣∣
Ionic radii of X⊕ and YΘ, respectively, are
0.35 and 0.68Å
0.68 and 0.35Å
1.20 and 0.80Å
0.80 and 1.20Å
The correct Answer is:C
To find the ionic radii of X2− and Y2− for the compounds AX and AY with rock salt type structure, we can follow these steps:
Step 1: Determine the Edge Lengths
For the rock salt structure, the anion-anion distance is related to the edge length a of the cubic unit cell. The relationship is given by:
Anion-Anion Distance=a√2
For AX, the anion-anion distance is 2.40 Å:
2.40=a1√2⟹a1=2.40×√2=2.40×1.414≈3.4Å
For AY, the anion-anion distance is 1.63 Å:
1.63=a2√2⟹a2=1.63×√2=1.63×1.414≈2.30Å
Step 2: Calculate Cation-Anion Distances
The cation-anion distance is given by:
Cation-Anion Distance=a2
For AX, the cation-anion distance is 1.70 Å:
1.70=a12⟹a1=1.70×2=3.4Å(consistent with previous calculation)
For AY, the cation-anion distance is 1.15 Å:
1.15=a22⟹a2=1.15×2=2.30Å(consistent with previous calculation)
Step 3: Establish the Relationship Between Ionic Radii
In a rock salt structure, the ratio of the cation radius R+ to the anion radius R− is given by:
R+R−=0.414
Thus, we can express the cation radius in terms of the anion radius:
R+=0.414R−
Step 4: Set Up the Equation for AX
For AX:
R++R−=1.70Å
Substituting R+:
0.414R−+R−=1.70
(0.414+1)R−=1.70
1.414R−=1.70⟹R−=1.701.414≈1.20Å
Thus, the ionic radius of X2− is approximately 1.20Å.
Step 5: Set Up the Equation for AY
For AY:
R++R−=1.15Å
Substituting R+:
0.414R−+R−=1.15
(0.414+1)R−=1.15
1.414R−=1.15⟹R−=1.151.414≈0.81Å
Thus, the ionic radius of Y2− is approximately 0.8Å.
Final Results
- Ionic radius of X2− is approximately 1.20Å.
- Ionic radius of Y2− is approximately 0.8Å.
For the rock salt structure, the anion-anion distance is related to the edge length a of the cubic unit cell. The relationship is given by:
Anion-Anion Distance=a√2
For AX, the anion-anion distance is 2.40 Å:
2.40=a1√2⟹a1=2.40×√2=2.40×1.414≈3.4Å
1.63=a2√2⟹a2=1.63×√2=1.63×1.414≈2.30Å
The cation-anion distance is given by:
Cation-Anion Distance=a2
For AX, the cation-anion distance is 1.70 Å:
1.70=a12⟹a1=1.70×2=3.4Å(consistent with previous calculation)
1.15=a22⟹a2=1.15×2=2.30Å(consistent with previous calculation)
In a rock salt structure, the ratio of the cation radius R+ to the anion radius R− is given by:
R+R−=0.414
Thus, we can express the cation radius in terms of the anion radius:
R+=0.414R−
For AX:
R++R−=1.70Å
Substituting R+:
0.414R−+R−=1.70
(0.414+1)R−=1.70
1.414R−=1.70⟹R−=1.701.414≈1.20Å
Thus, the ionic radius of X2− is approximately 1.20Å.
For AY:
R++R−=1.15Å
Substituting R+:
0.414R−+R−=1.15
(0.414+1)R−=1.15
1.414R−=1.15⟹R−=1.151.414≈0.81Å
Thus, the ionic radius of Y2− is approximately 0.8Å.
- Ionic radius of X2− is approximately 1.20Å.
- Ionic radius of Y2− is approximately 0.8Å.
Topper's Solved these Questions
- SOLID STATEBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLID STATEExercise:Exercises (Multiple Correct)
Explore 39 Videos
- SOLID STATEBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLID STATEExercise:Exercises (Single Correct)
Explore 72 Videos
- SOLID STATEBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLID STATEExercise:Solved Examples
Explore 13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBook:CENGAGE CHEMISTRY ENGLISHChapter:REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSExercise:SUBJECTIVE TYPE
Explore 4 Videos
- SOLUTIONSBook:CENGAGE CHEMISTRY ENGLISHChapter:SOLUTIONSExercise:Ex 2.3 (Objective)
Explore 9 Videos
Similar Questions
AX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
Ionic radii of A⊕ and B⊕, respectively, are
a.0.35 and 0.68Å
b.0.68 and 0.35Å
c.1.20 and 0.80Å
d.0.80 and 1.20Å
View SolutionAX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
Which of the following structure is, respectively, by Ax?
(a)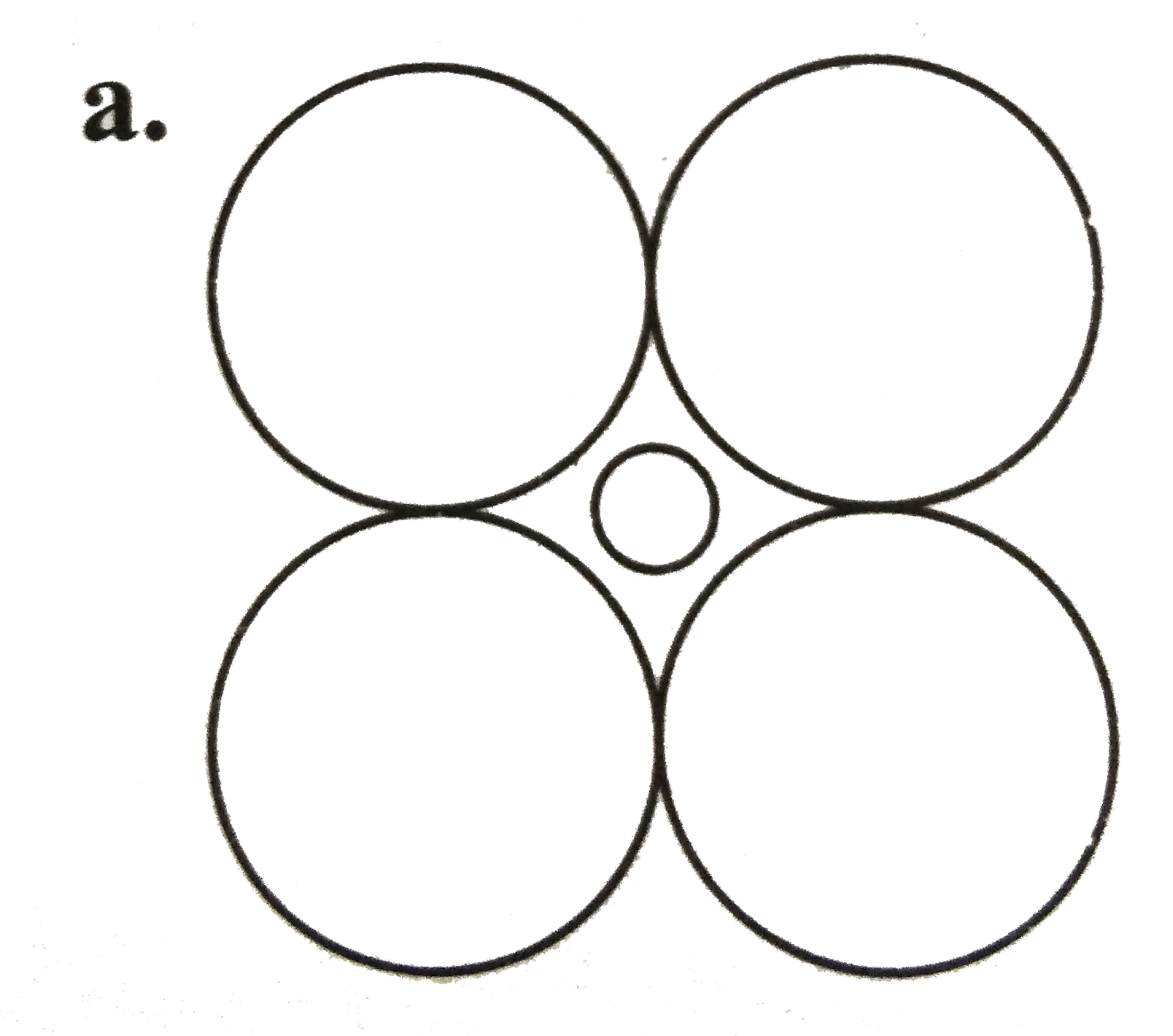
(b)
(c)
(d)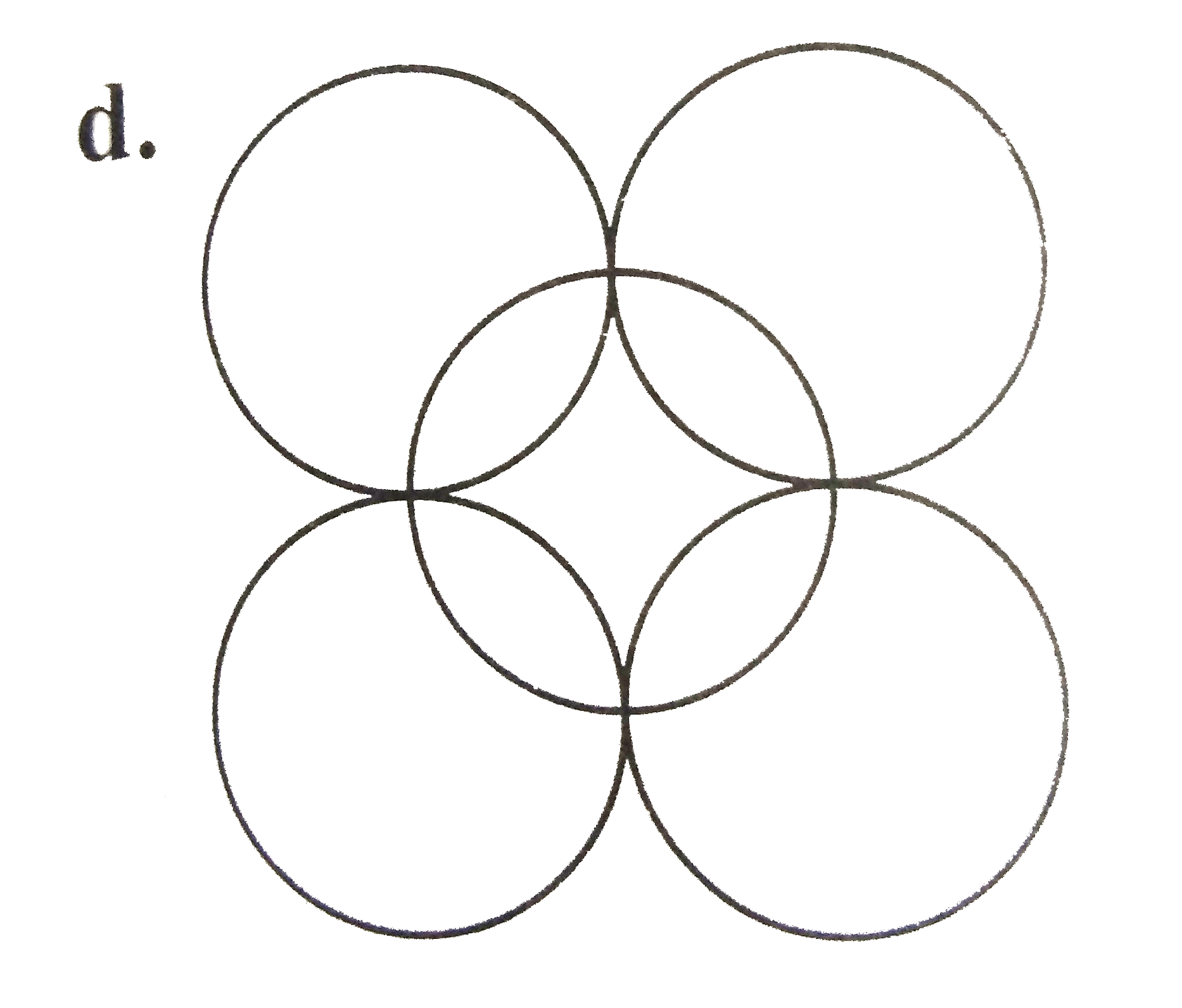
View Solution
Knowledge Check
If f(x) =ax2+bx+c and f(1)=3 and f(-1)=3, then a+c equals
A-3B0C2D3
AX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
The structure given below is of

(a)AX
(b)AY,BX
(c)AY,BX,BY
(d)AY,BX,BYandKCI
View SolutionAX,AY,BX, and BY have rock salt type structure with following internuclear distances:
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣SaltAnion-anionCation-aniondistance inÅdistance inÅAX2.401.70AY1.631.15BX2.661.88By2.091.48∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
A salt MY crystallizes in the CsCl structure. The anions at the corners touch each other and cation is in the centre. The radius ratio (r⊕/rΘ) for this structure is
View SolutionSuggest the probable structures of the unit cells of the following each compound with the help of given data
∣∣ ∣ ∣ ∣ ∣ ∣∣Cationic radiusAnionic radius(a)RbBe1.04Å1.95Å(b)MeTe0.65Å2.21Å(c)MgO0.65Å1.40Å(d)BaO1.35Å1.40Å∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionIf Ax+By=1 is a normal to the curve ay=x2, then :
View SolutionDIfferentiate the following w.r.t x :1ax2+bx+c
View SolutionAssertion:- Antifluorite structure is 4:8 (cation:anion) type coordination crystal.
Reason:- Ratio of no. of cation and anions in CaF2 crystal is 1:2
View SolutionThe crystal AB(rock salt structure) has molecular weight 6.023Yu, where Y is an arbitrary number in u. If the minimum distance between cation and anion is Y13nm. Find the density in kgm−3.
View Solution