Which of the following statements is//are correct about in an fcc unit cell?
Given: Edge length
Body diagonai
Each lies at a diastance b//4 from the nearest corner.
Each lies at a distance from the farthest corner.
Each lies at a distance of from the nearest corner.
The distance between two is .
The correct Answer is:A, B, C, D
To solve the question regarding the tetrahedral voids in a face-centered cubic (FCC) unit cell, we will analyze the given statements one by one based on the properties of FCC lattices.
1. Understanding FCC Unit Cell:
- In an FCC unit cell, atoms are located at each of the corners and the centers of each face of the cube.
- The edge length of the cube is given as a, and the body diagonal is given as b.
2. Finding the Body Diagonal:
- The body diagonal b of a cube can be calculated using the formula:
\(
b = \sqrt{a^2 + a^2 + a^2} = a\sqrt{3}
\)
- Therefore, \( b = a\sqrt{3} \).
3. Position of Tetrahedral Voids:
- In an FCC unit cell, there are 8 tetrahedral voids. The positions of these voids can be determined based on the arrangement of the atoms.
- The tetrahedral voids are located at specific fractional coordinates within the unit cell.
4. Analyzing Each Statement:
- Option 1: Each tetrahedral void lies at a distance of \( \frac{b}{4} \) from the nearest corner.
- The distance from the corner to the tetrahedral void is indeed \( \frac{b}{4} \). This statement is correct.
- Option 2: Each tetrahedral void lies at a distance of \( \frac{3b}{4} \) from the farthest corner.
- The distance from the farthest corner can be calculated as \( b - \frac{b}{4} = \frac{3b}{4} \). This statement is correct.
- Option 3: Each tetrahedral void lies at a distance of \( \frac{\sqrt{3}a}{4} \) from the nearest corner.
- Since \( b = a\sqrt{3} \), we have \( \frac{b}{4} = \frac{a\sqrt{3}}{4} \), which is equivalent to \( \frac{\sqrt{3}a}{4} \). This statement is correct.
- Option 4: The distance between two tetrahedral voids is \( \frac{b}{2} \).
- The distance between two tetrahedral voids can be calculated based on their positions. It is found to be \( \frac{b}{2} \). This statement is correct.
5. Conclusion:
- All the statements regarding the tetrahedral voids in an FCC unit cell are correct.
Final Answer:
All options are correct regarding the tetrahedral voids in an FCC unit cell.
---
- In an FCC unit cell, atoms are located at each of the corners and the centers of each face of the cube.
- The edge length of the cube is given as a, and the body diagonal is given as b.
- The body diagonal b of a cube can be calculated using the formula:
\(
b = \sqrt{a^2 + a^2 + a^2} = a\sqrt{3}
\)
- Therefore, \( b = a\sqrt{3} \).
- In an FCC unit cell, there are 8 tetrahedral voids. The positions of these voids can be determined based on the arrangement of the atoms.
- The tetrahedral voids are located at specific fractional coordinates within the unit cell.
- Option 1: Each tetrahedral void lies at a distance of \( \frac{b}{4} \) from the nearest corner.
- The distance from the corner to the tetrahedral void is indeed \( \frac{b}{4} \). This statement is correct.
- Option 2: Each tetrahedral void lies at a distance of \( \frac{3b}{4} \) from the farthest corner.
- The distance from the farthest corner can be calculated as \( b - \frac{b}{4} = \frac{3b}{4} \). This statement is correct.
- Option 3: Each tetrahedral void lies at a distance of \( \frac{\sqrt{3}a}{4} \) from the nearest corner.
- Since \( b = a\sqrt{3} \), we have \( \frac{b}{4} = \frac{a\sqrt{3}}{4} \), which is equivalent to \( \frac{\sqrt{3}a}{4} \). This statement is correct.
- Option 4: The distance between two tetrahedral voids is \( \frac{b}{2} \).
- The distance between two tetrahedral voids can be calculated based on their positions. It is found to be \( \frac{b}{2} \). This statement is correct.
- All the statements regarding the tetrahedral voids in an FCC unit cell are correct.
All options are correct regarding the tetrahedral voids in an FCC unit cell.
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Single Correct)
72 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Assertion-Reasoning)
19 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)
13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
4 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
Knowledge Check
Which of the following statement is not correct about an inert electrode in a cell?
AIt does not participate in the cell reaction.BIt provides surface either for oxidation or for reduction reaction.CIt provides surface for conduction of electrons.DIt provide surface for redox reaction
Which of the following statements are correct about the following reaction
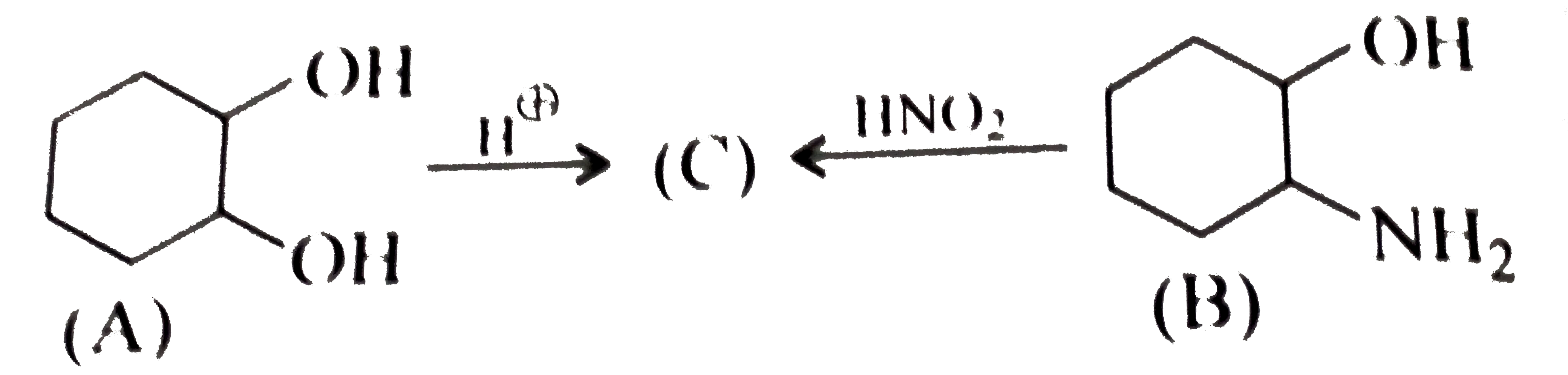
View SolutionWhich of the following statement is correct about the given Daniell cell?

View SolutionWhich of the following statements is incorrect about generative cell?
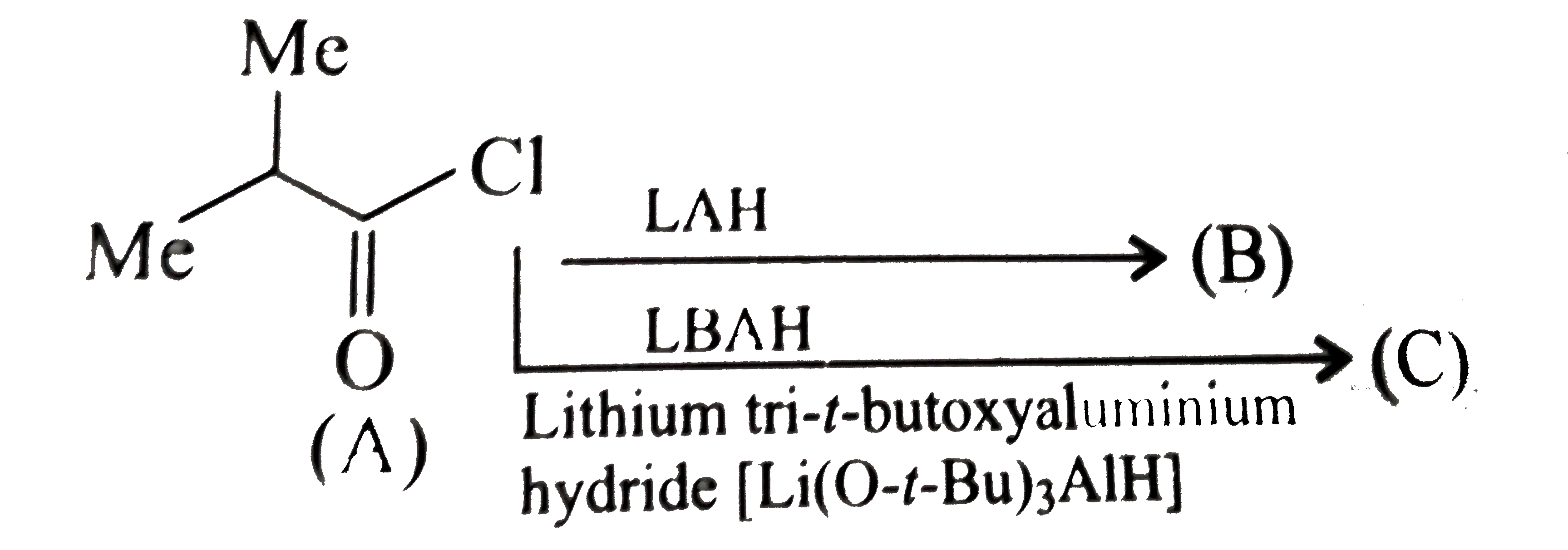
View SolutionWhich of the following statements are correct about the following reaction ?
View SolutionWhich of the following statements are correct about the reaction given below ?

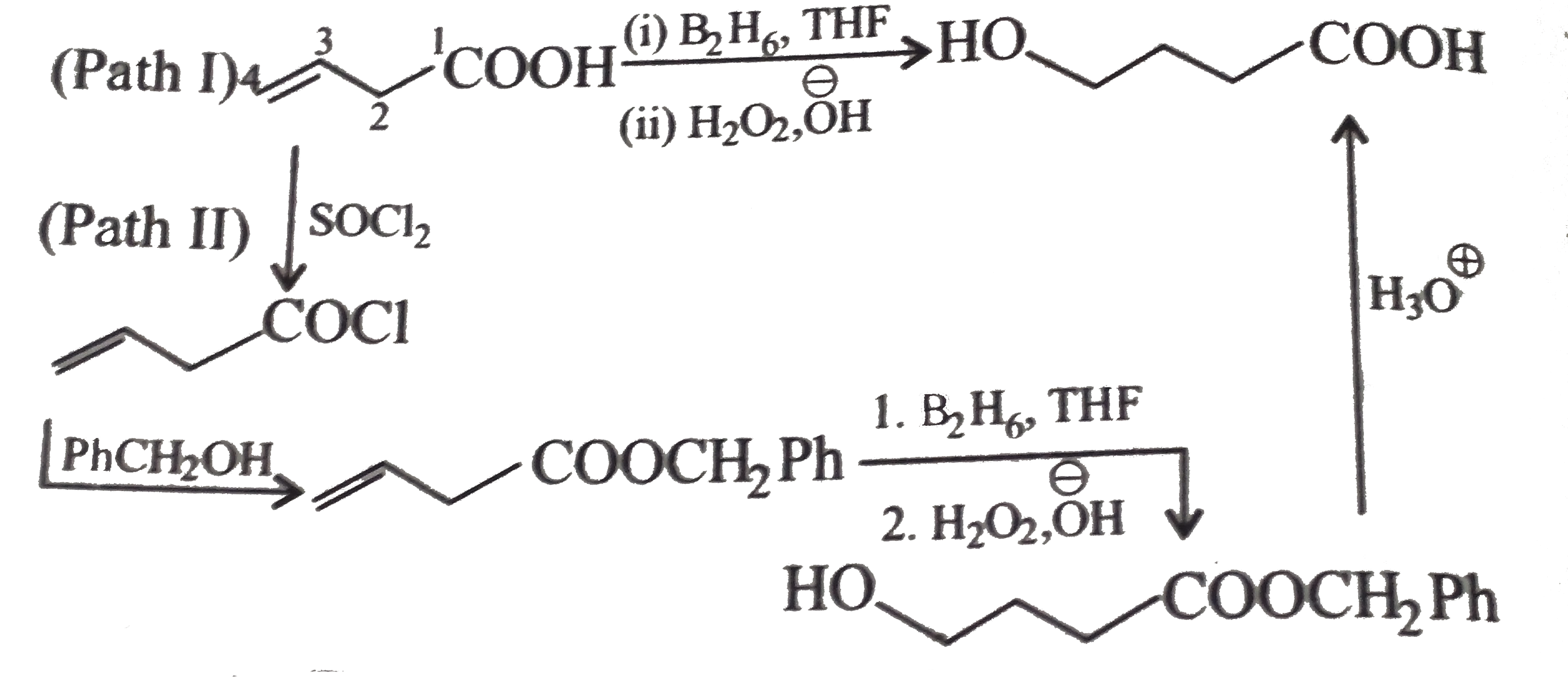
View SolutionWhich of the following statements are correct about the following reactions :
 .
.
View SolutionWhich of the following statements is wrong about galvanic cells?
View Solution
