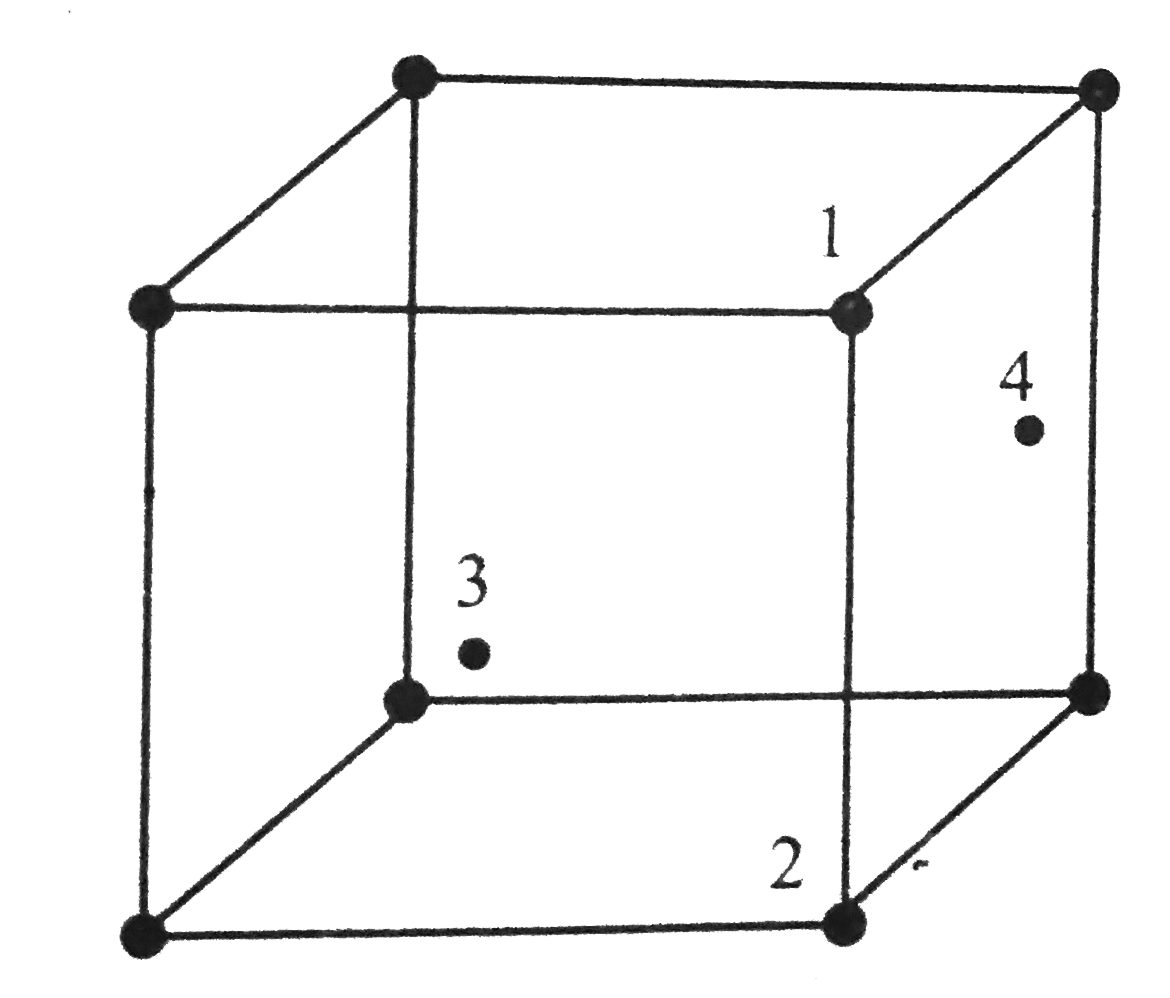
In fcc unit cell, atoms are numbered as shown below.
The atoms not touching each other are (Atom numbered 3 is face centre of front face)

3 and 4
1 and 3
1 and 2
2 and 4
The correct Answer is:C
In fcc structure, corner atoms do not touch each other (atom 1 and 2), but every face centre aton touches corners. Moreover, every face center atom touches every other face centre atom in an fcc unit cell.
i. Atoms 3 and 4 are 4 are touching each other where centre-to-centre distance =a√2
ii. Atoms 1 and 2 are not touching each other.
iii. Atoms 2 and 4 are touching each other where centre-to-centre distance =a√2
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Assertion-Reasoning)
19 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Interger)
9 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Multiple Correct)
39 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
4 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
Knowledge Check
The total number of tetrahedral voids in the face centred unit cell is
A6B8C10D12
A unit cell consists of a cube in which the atoms A are occupying the corners while the atoms B are present at the centre of each face. If the atoms A are missing from 2 corners, what is the simplest formuls of the compound ?
View SolutionThe 2D unit cell of an element is shown. The two layers are placed one over the other and touching each other. Find the effective number of atoms in the unit cell
View SolutionHow many unit cells are shared by an atom on the face of a unit cell?
View SolutionIn a cubic type unit cell, A atoms are at one half faces, while B atoms are at the corners of the cube. Calculate the formula of the compound.
View SolutionSilver crystallizes in face-centred cubic unit cell. Each side of this unit cell has a length of 400 pm. Calculate the radius of the silver atom. (Assume the atoms touch each other on the diagonal across the face of the unit cell. That is each face atom is touching the four corner atoms).
View SolutionSilver crystallises in a face centred cubic unit cell. Each side of the unit cell has a length of 500 pm. Calculate radius of the silver atoms (Assume that the atoms just touch each other on the diagonal across the face of the unit cell i.e. each face atom is touching four atoms)
View SolutionIn a face centered cubic arrangement of A and B atoms whose A atoms are at the corner of the unit cell and B atoms at the face centers. One of the B atoms missing from one of the face in unit cell. The simplest formula of compounding is:
View Solution