Find the number of hexagonal faces that are present in a truncated octahedral.
To find the number of hexagonal faces in a truncated octahedron, we can follow these steps:
1. Understand the Definition: A truncated octahedron is a type of Archimedean solid that has both hexagonal and square faces. It is formed by truncating (cutting off) the vertices of a regular octahedron.
2. Visualize the Structure: To count the hexagonal faces, it is helpful to visualize or draw the structure of a truncated octahedron. It has a specific geometric shape that can be represented in 3D.
3. Identify the Faces: In a truncated octahedron, there are two types of faces: hexagonal and square. We need to focus on identifying the hexagonal faces.
4. Count the Hexagonal Faces: As we examine the structure:
- There are hexagonal faces located at various positions on the solid.
- By systematically counting, we find:
- One hexagonal face on the front,
- One on the back,
- One on the top,
- One on the bottom,
- One on each of the four sides.
5. Total Count: After counting all the hexagonal faces, we find that there are a total of 8 hexagonal faces in a truncated octahedron.
Final Answer:
The number of hexagonal faces in a truncated octahedron is 8.
---
- There are hexagonal faces located at various positions on the solid.
- By systematically counting, we find:
- One hexagonal face on the front,
- One on the back,
- One on the top,
- One on the bottom,
- One on each of the four sides.
The number of hexagonal faces in a truncated octahedron is 8.
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Archives ) Subjective9videos
SOLID STATE
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Ex 1.1 (Subjective)12videos
SOLID STATE
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Archives ) Assertion-Reasoning1videos
SOLID STATE
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE4videos
REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)9videos
SOLUTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Assertion:A tetrahedral void is surrounded by four spheres and an octahedral void is surrounded by six spheres.
Reason:The number of tetrahedral voids is double the number of close packed spheres and number of octahedral voids is equal to number of close packed spheres.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false
Find out the number of unpaired electrons in strong and weak octahedral for Cr3+ and Fe2+ ions .
View SolutionThe number of octahedral sites per sphere in fcc structure is
View SolutionFind out number of stereogenic centers present in following compound.
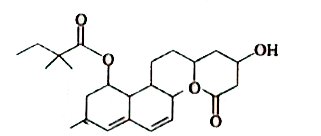 View Solution
View SolutionTotal number of faces in a truncated octahedron=x
Total number of faces in a truncated tetrahedron=y
Then x+y is :View SolutionHow many hexagonal ommatidia are present in each compound eye of cockroach?
View SolutionThe total number of octahedral void (s) per atom present in a cubic close packed structure is
View SolutionThe total number of octahedral void (s) per atom present in a cubic close packed structure is
View Solution

