The molar conductivity of KCl solution at different concentrations at 298K is given below :
corM(molL−1)∧m(Scm2mol−1)0.000198148.610.000309148.290.000521147.810.000989147.09
Show that a plot between ∧m and √c is a straight line. Determine the value of ∧∘m and A for KCl .
To solve the problem, we need to show that a plot between the molar conductivity (λ_m) and the square root of concentration (√c) is a straight line, and then determine the values of λ_m0 and A for KCl.
1. Calculate the Square Root of Concentration (√c):
- Given concentrations (c in mol/L):
- 0.000198
- 0.000309
- 0.000521
- 0.000989
- Calculate √c for each concentration:
- √(0.000198) ≈ 0.01407
- √(0.000309) ≈ 0.01758
- √(0.000521) ≈ 0.02285
- √(0.000989) ≈ 0.0314
2. List the Molar Conductivity (λ_m):
- Given λ_m values corresponding to the concentrations:
- 148.61
- 148.29
- 147.81
- 147.09
3. Plotting the Values:
- Plot λ_m on the y-axis and √c on the x-axis.
- The points to plot are:
- (0.01407, 148.61)
- (0.01758, 148.29)
- (0.02285, 147.81)
- (0.0314, 147.09)
4. Determine the Equation of the Line:
- The relationship between λ_m and √c can be expressed as:
λm=λ0m−A⋅√c
- Where λ_m^0 is the intercept (value of λ_m when √c = 0) and A is the slope of the line.
5. Finding λ_m^0:
- From the plot, we can estimate λ_m^0 (the y-intercept) to be approximately 150 S cm² mol⁻¹.
6. Calculating the Slope (A):
- Use two points to calculate the slope (A):
- Let (x1, y1) = (0.01407, 148.61) and (x2, y2) = (0.0314, 147.09).
- The slope A is given by:
A=−y2−y1x2−x1=−147.09−148.610.0314−0.01407
- Calculate:
A=−−1.520.01733≈87.7S cm2mol−1L1/2
Final Results:
- The plot of λ_m vs. √c is a straight line.
- The values are:
- λ_m^0 ≈ 150 S cm² mol⁻¹
- A ≈ 87.7 S cm² mol⁻¹ L^(1/2)
- Given concentrations (c in mol/L):
- 0.000198
- 0.000309
- 0.000521
- 0.000989
- Calculate √c for each concentration:
- √(0.000198) ≈ 0.01407
- √(0.000309) ≈ 0.01758
- √(0.000521) ≈ 0.02285
- √(0.000989) ≈ 0.0314
- Given λ_m values corresponding to the concentrations:
- 148.61
- 148.29
- 147.81
- 147.09
- Plot λ_m on the y-axis and √c on the x-axis.
- The points to plot are:
- (0.01407, 148.61)
- (0.01758, 148.29)
- (0.02285, 147.81)
- (0.0314, 147.09)
- The relationship between λ_m and √c can be expressed as:
λm=λ0m−A⋅√c
- Where λ_m^0 is the intercept (value of λ_m when √c = 0) and A is the slope of the line.
- From the plot, we can estimate λ_m^0 (the y-intercept) to be approximately 150 S cm² mol⁻¹.
- Use two points to calculate the slope (A):
- Let (x1, y1) = (0.01407, 148.61) and (x2, y2) = (0.0314, 147.09).
- The slope A is given by:
A=−y2−y1x2−x1=−147.09−148.610.0314−0.01407
- Calculate:
A=−−1.520.01733≈87.7S cm2mol−1L1/2
- The plot of λ_m vs. √c is a straight line.
- The values are:
- λ_m^0 ≈ 150 S cm² mol⁻¹
- A ≈ 87.7 S cm² mol⁻¹ L^(1/2)
Topper's Solved these Questions
- ELECTROCHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Solved Examples (Electrochemical Cell)
36 Videos
- ELECTROCHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Solved Examples(Electrolysis And Electrolytic Cells)
12 Videos
- D AND F BLOCK ELEMENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Archives Subjective
29 Videos
- GENERAL PRINCIPLES AND PROCESS OF ISOLATION OF ELEMENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - GENERAL PRINCIPLES AND PROCESS OF ISOLATION OF ELEMENTSEXERCISE - Archives (Subjective)
14 Videos
Similar Questions
The molar conductivity of KCl solutions at different concentration at 298K are given below :
C/mol L−1∧m/Scm2mol−10.000198148.610.000309148.290.000521147.810.000987143.09
Show that a plot between ∧mandC1/2 is a straight line. Determine the values of ∧0mand∧ for KCl.
View SolutionThe pressure-volume of varies thermodynamic process is shown in graphs:
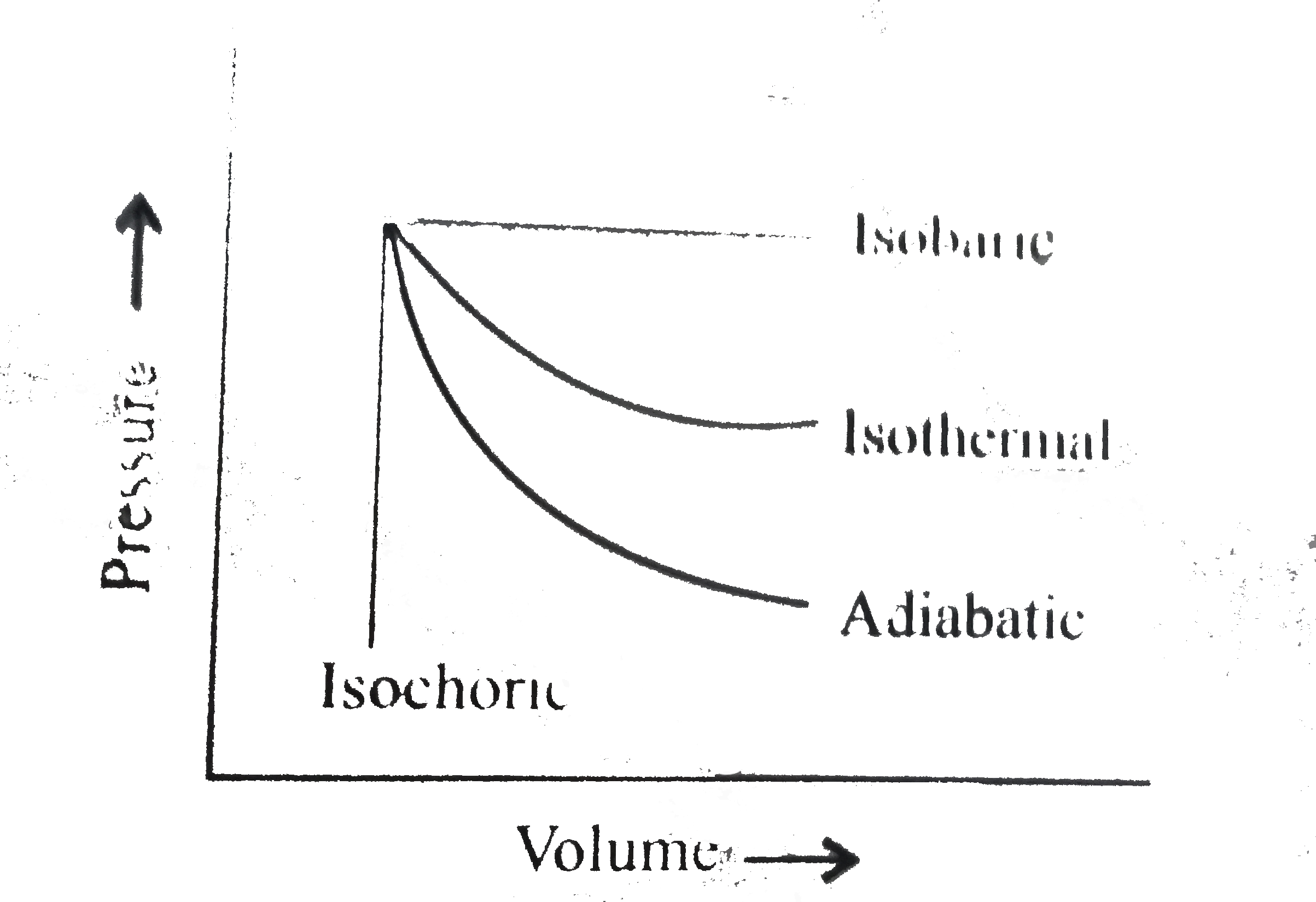
Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
wrev>wirr
The works of isothermal and adiabatic processes are different from each other.
wisothermal reversible=−2.303nRTlog10(V2V1)
=2.303nRTlog10(P2P1)
wadiabatic reversible=CV(T1−T2)
Calculate work done when 1 mole of an ideal gas is expanded reversibly from 30L to 60L at a constant temperature of 300K
View Solution
Knowledge Check
Molar conductivity of 0.15 M solution of KCI at 298 K, if its conductivity is 0.0152 S cm−1 will be
A124Ω−1cm2mol−1B204Ω−1cm2mol−1C101Ω−1cm2mol−1D300Ω−1cm2mol−1
The conductivity of a 0.01 M solution of acetic acid at 298 k is 1.65×10−4Scm−1. Calculate molar conductivity (∧m) of the solution.
View SolutionThe conductivity of a 0.01 M solution of acetic acid at 298 k is 1.65×10−4Scm−1. Calculate molar conductivity (∧m)of the solution.
View SolutionThe conductivity of 0.10 M solution of KCl at 298 K is 0.025 S cm Calculate its molar conductivity.
View SolutionThe conductivity of 0.20 M solution of KCl at 298 K is 0.0248 S cm−1 . Calculate its molar conductivity.
View SolutionThe conductivity of 0.20 M solution of KCl at 298 K is 0.0248 S cm−1 . Calculate its molar conductivity.
View SolutionThe conductivity of 0.20 M solution of KCl at 298 K is 0.025 S cm−1. Calculate its molar conductivity.
View SolutionThe boiling point of 0.1MKCl solution is ………..than 100∘C.
View Solution
