The combustion of butane in O2 at 1 bar and 298K shows a decrease in free energy equal to 2.95×103kJmol−1 in a fuel cell. K and Ec− of the fuel cell are
9.55×10482,1.096V
9.55,1.096V
1.023×10966,2.85V
5.5×10484,0.55V
The correct Answer is:a
To solve the question regarding the combustion of butane in a fuel cell, we need to find the equilibrium constant (K) and the cell potential (E°) for the reaction. The given information states that the change in free energy (ΔG) is -2.95 x 10^3 kJ/mol.
Step 1: Relate ΔG to K
The relationship between the change in free energy (ΔG) and the equilibrium constant (K) is given by the equation:
ΔG=−RTlnK
Where:
- R is the universal gas constant (8.314 J/(mol·K))
- T is the temperature in Kelvin (298 K)
Step 2: Convert ΔG to Joules
Since R is in J/(mol·K), we need to convert ΔG from kJ to J:
ΔG=−2.95×103 kJ/mol=−2.95×106 J/mol
Step 3: Solve for K
Now we can rearrange the equation to solve for K:
K=e−ΔG/(RT)
Substituting the values:
- R=8.314 J/(mol⋅K)
- T=298 K
- ΔG=−2.95×106 J/mol
Calculating:
K=e−(−2.95×106)/(8.314×298)
K=e(2.95×106)/(2477.572)
K=e1190.16
Step 4: Calculate K
Using a calculator:
K≈e1190.16
This value is extremely large, indicating that the reaction strongly favors products at equilibrium.
Step 5: Relate ΔG to E°
The relationship between ΔG and the standard cell potential (E°) is given by:
ΔG=−nFE°
Where:
- n is the number of moles of electrons transferred in the reaction
- F is the Faraday constant (approximately 96485 C/mol)
Step 6: Solve for E°
Rearranging the equation gives:
E°=−ΔGnF
Assuming that the combustion of butane involves 2 moles of electrons (this can vary based on the specific reaction):
E°=−−2.95×106 J/mol2×96485 C/mol
Calculating:
E°=2.95×106192970
E°≈15.29 V
Final Results
- The equilibrium constant K is extremely large, indicating a strong favorability for the products.
- The standard cell potential E° is approximately 15.29 V.
The relationship between the change in free energy (ΔG) and the equilibrium constant (K) is given by the equation:
ΔG=−RTlnK
Where:
- R is the universal gas constant (8.314 J/(mol·K))
- T is the temperature in Kelvin (298 K)
Since R is in J/(mol·K), we need to convert ΔG from kJ to J:
ΔG=−2.95×103 kJ/mol=−2.95×106 J/mol
Now we can rearrange the equation to solve for K:
K=e−ΔG/(RT)
Substituting the values:
- R=8.314 J/(mol⋅K)
- T=298 K
- ΔG=−2.95×106 J/mol
K=e−(−2.95×106)/(8.314×298)
K=e(2.95×106)/(2477.572)
K=e1190.16
Using a calculator:
K≈e1190.16
This value is extremely large, indicating that the reaction strongly favors products at equilibrium.
The relationship between ΔG and the standard cell potential (E°) is given by:
ΔG=−nFE°
Where:
- n is the number of moles of electrons transferred in the reaction
- F is the Faraday constant (approximately 96485 C/mol)
Rearranging the equation gives:
E°=−ΔGnF
Assuming that the combustion of butane involves 2 moles of electrons (this can vary based on the specific reaction):
E°=−−2.95×106 J/mol2×96485 C/mol
E°=2.95×106192970
E°≈15.29 V
- The equilibrium constant K is extremely large, indicating a strong favorability for the products.
- The standard cell potential E° is approximately 15.29 V.
Topper's Solved these Questions
- ELECTROCHEMISTRYBook:CENGAGE CHEMISTRY ENGLISHChapter:ELECTROCHEMISTRYExercise:Exerciseassertion -Reasoning
Explore 25 Videos
- ELECTROCHEMISTRYBook:CENGAGE CHEMISTRY ENGLISHChapter:ELECTROCHEMISTRYExercise:Exerciseinterger
Explore 8 Videos
- ELECTROCHEMISTRYBook:CENGAGE CHEMISTRY ENGLISHChapter:ELECTROCHEMISTRYExercise:Exercisemultiple Correct Ansers
Explore 53 Videos
- D AND F BLOCK ELEMENTSBook:CENGAGE CHEMISTRY ENGLISHChapter:D AND F BLOCK ELEMENTSExercise:Archives Subjective
Explore 29 Videos
- GENERAL PRINCIPLES AND PROCESS OF ISOLATION OF ELEMENTSBook:CENGAGE CHEMISTRY ENGLISHChapter:GENERAL PRINCIPLES AND PROCESS OF ISOLATION OF ELEMENTSExercise:Archives (Subjective)
Explore 14 Videos
Similar Questions
The enthalpy of combustion of benzoic acid (C6H5COOH) at 298K and 1atm pressure is −2500.0kJmol−1. What is ΔU for the reaction?
View SolutionThe standard state Gibbs free energies of formation of ) C(graphite and C(diamond) at T = 298 K are
ΔfG∘[C(graphite)]=0kJmol−1
ΔfG∘[C(diamond)]=2.9kJmol−1
The standard state means that the pressure should be 1 bar, and substance should be pure at a given temperature. The conversion of graphite [ ) C(graphite ] to diamond [C(diamond)] reduces its volume by 2×10−6m3mol−1. If ) C(graphite is converted to C(diamond) isothermally at T = 298 K, the pressure at which ) C(graphite is in equilibrium with C(diamond), is
[Useful information:1J=1kgm2s−2,1Pa=1kgm−1s−2,1bar=105Pa]
View SolutionThe enthalpies of combustion of carbon and carbon monoxide in excess of oxygen at 298K and constant pressure are −393.5 and −283.0kJmol−1, respectively. Calculate the heat of formation of carbon monoxide at constant volume.
View SolutionRate constant k=1.2×103mol−1Ls−1 and Ea=2.0×102kJmol−1. When T→∞:
View SolutionIn a fuel cell methanol is used as fuel and oxygen gas is used as an oxidizer. The reaction is :
CH3OH(l)+32O2(g)→CO2((g))+2H2O(l)
At 298K standard Gibb's energies of formation for CH3OH(l),H2O(l) and CO2(g) are −166.2,−237.2 and −394.4kJmol−1 respectively. If standard enthalpy of combustion of methanol is −726kJmol−1, efficiency of the fuel cell will be :
View SolutionIn a fuel cell methanol is used as fuel and oxygen gas is used as an oxidizer. The reaction is :
CH3OH(l)+32O2(g)→CO2((g))+2H2O(l)
At 298K standard Gibb's energies of formation for CH3OH(l),H2O(l) and CO2(g) are −166.2,−237.2 and −394.4kJmol−1 respectively. If standard enthalpy of combustion of methanol is −726kJmol−1, efficiency of the fuel cell will be :
View SolutionIn a fuel cell methanol is used as fuel and oxygen gas is used as an oxidizer. The reaction is :
CH3OH(l)+32O2(g)→CO2((g))+2H2O(l)
At 298K standard Gibb's energies of formation for CH3OH(l),H2O(l) and CO2(g) are −166.2,−237.2 and −394.4kJmol−1 respectively. If standard enthalpy of combustion of methanol is −726kJmol−1, efficiency of the fuel cell will be :
View SolutionIn a fuel cell methanol is used as fuel and oxygen gas is used as an oxidizer. The reaction is :
CH3OH(l)+32O2(g)→CO2((g))+2H2O(l)
At 298K standard Gibb's energies of formation for CH3OH(l),H2O(l) and CO2(g) are −166.2,−237.2 and −394.4kJmol−1 respectively. If standard enthalpy of combustion of methanol is −726kJmol−1, efficiency of the fuel cell will be :
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
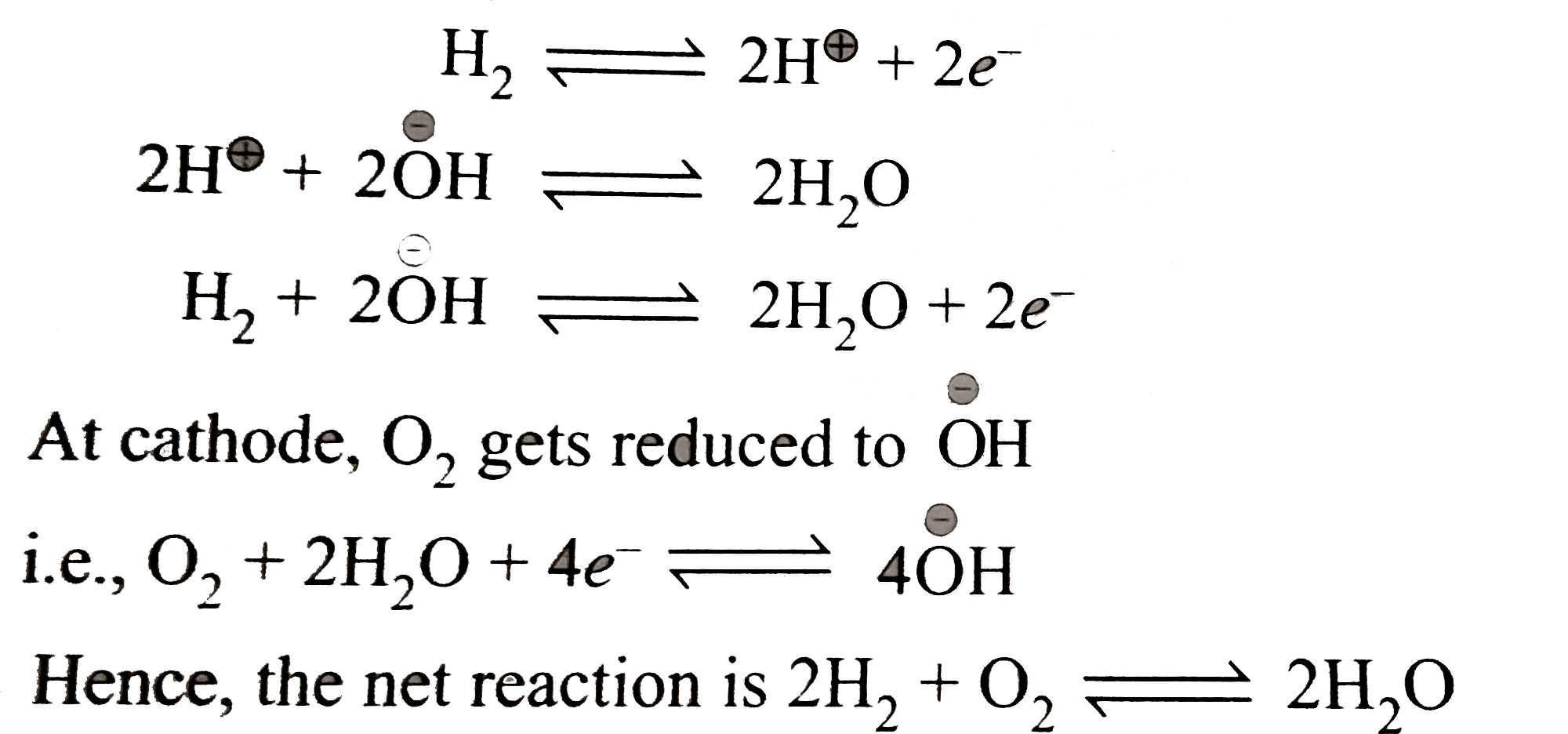
At cathode, O2 gets reduced to c−OH
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
What is the value of ΔSc− for the fuel cell at 25∘C?
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
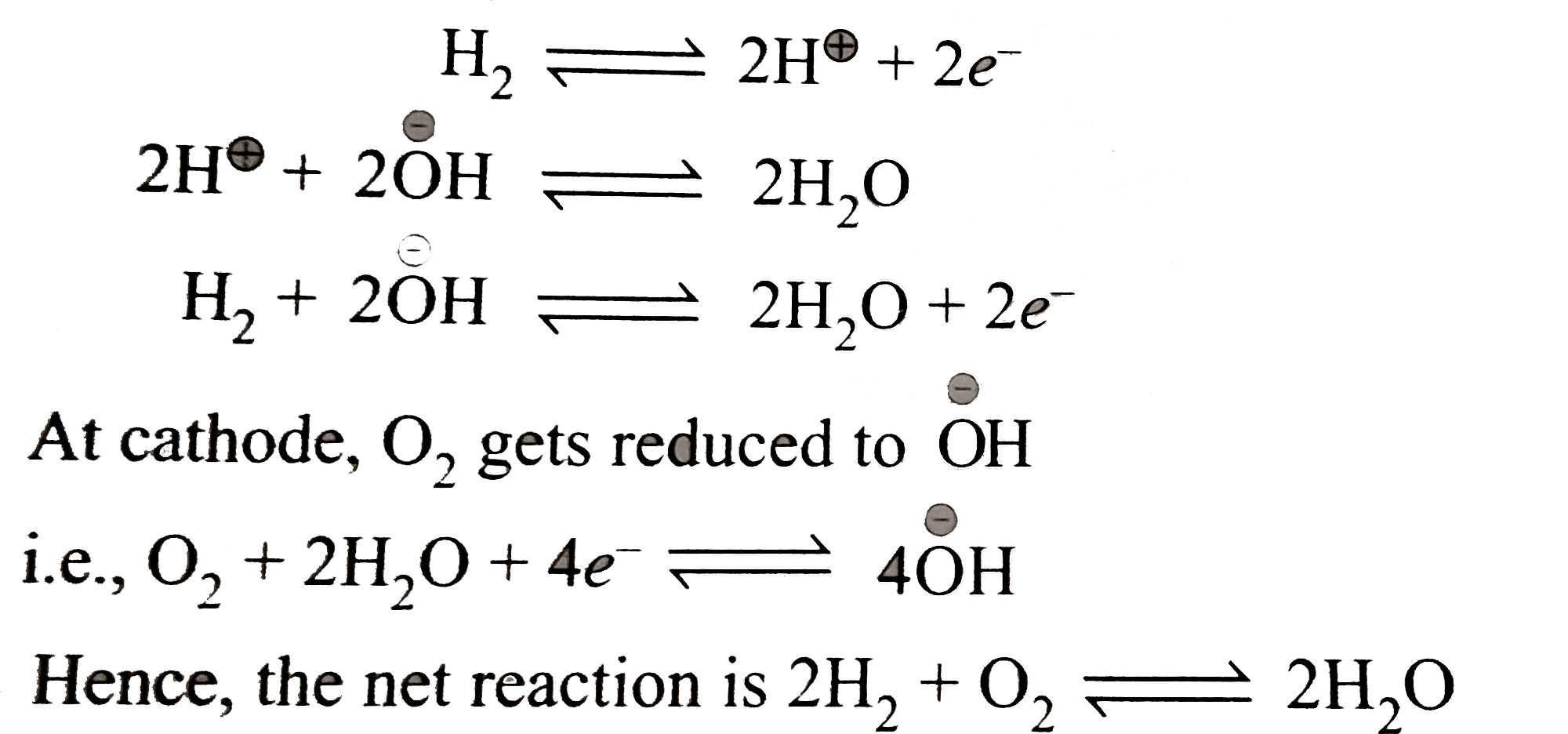
At cathode, O2 gets reduced to c−OH
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
What is the value of ΔSc− for the fuel cell at 25∘C?
a.−1600JK−1
b.−160JK−1
c.160JK−1
d.1600JK−1
View Solution
