For the non-equilibrium process, A+B→ Product, the rate is first-order w.r.t. A and second order w.r.t. B. If 1.0mol each of A and B were inrofuced into 1.0L vessel and the initial rate was 1.0×10−2molL−1s−1, calculate the rate when half the reactants have been turned into Products.
To solve the problem, we need to calculate the rate of the reaction when half of the reactants A and B have been converted into products. Let's go through the steps systematically.
Step 1: Write the Rate Law Expression
The rate of the reaction is given as first-order with respect to A and second-order with respect to B. Therefore, the rate law can be expressed as:
Rate=k(A)1(B)2
Step 2: Determine Initial Concentrations
Initially, we have 1.0 mol of A and 1.0 mol of B in a 1.0 L vessel. Thus, the initial concentrations of A and B are:
(A)0=1.0mol1.0L=1.0M
(B)0=1.0mol1.0L=1.0M
Step 3: Calculate the Rate Constant (k)
We know the initial rate of the reaction is 1.0×10−2mol L−1s−1. Substituting the initial concentrations into the rate law:
1.0×10−2=k(1.0)1(1.0)2
This simplifies to:
1.0×10−2=k⋅1⋅1
Thus, we find:
k=1.0×10−2mol−1Ls−1
Step 4: Determine Concentrations When Half the Reactants are Used
When half of A and B have been converted to products, the concentrations of A and B will be:
(A)=1.0−0.5=0.5M
(B)=1.0−0.5=0.5M
Step 5: Calculate the New Rate
Now we can substitute these new concentrations into the rate law to find the new rate:
Rate=k(A)1(B)2
Substituting the values we have:
Rate=(1.0×10−2)(0.5)1(0.5)2
Calculating this gives:
Rate=(1.0×10−2)(0.5)(0.25)=(1.0×10−2)×0.125
Rate=1.25×10−3mol L−1s−1
Final Answer
The rate when half the reactants have been turned into products is:
Rate=1.25×10−3mol L−1s−1
---
The rate of the reaction is given as first-order with respect to A and second-order with respect to B. Therefore, the rate law can be expressed as:
Initially, we have 1.0 mol of A and 1.0 mol of B in a 1.0 L vessel. Thus, the initial concentrations of A and B are:
(B)0=1.0mol1.0L=1.0M
We know the initial rate of the reaction is 1.0×10−2mol L−1s−1. Substituting the initial concentrations into the rate law:
When half of A and B have been converted to products, the concentrations of A and B will be:
(B)=1.0−0.5=0.5M
Now we can substitute these new concentrations into the rate law to find the new rate:
The rate when half the reactants have been turned into products is:
Topper's Solved these Questions
- CHEMICAL KINETICSBook:CENGAGE CHEMISTRY ENGLISHChapter:CHEMICAL KINETICSExercise:Solved Example
Explore 52 Videos
- CHEMICAL KINETICSBook:CENGAGE CHEMISTRY ENGLISHChapter:CHEMICAL KINETICSExercise:Ex 4.1 (Objective)
Explore 9 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBook:CENGAGE CHEMISTRY ENGLISHChapter:CARBOXYLIC ACIDS AND THEIR DERIVATIVESExercise:Exercises Archives (Analytical And Descriptive)
Explore 34 Videos
- COORDINATION COMPOUNDSBook:CENGAGE CHEMISTRY ENGLISHChapter:COORDINATION COMPOUNDSExercise:Archives Subjective
Explore 18 Videos
Similar Questions
Knowledge Check
The rate of first order reaction is 1.5×10−2 molL−1−1min at 0.5 M concentration of the reactant. The half-life of the reaction is
A7.53 minB0.383minC23.1 minD8.73 minThe rate of first order reaction is 1.5×10−2 molL−1−1min at 0.5 M concentration of the reactant. The half-life of the reaction is
A7.53 minB0.383minC23.1 minD8.73 minThe rate of first order reaction is 1.5×10−2 molL−1−1min at 0.5 M concentration of the reactant. The half-life of the reaction is
A7.53 minB0.383minC23.1 minD8.73 min
The rate of a first order reaction is 1.5×10−2molL−1min−1 at 0.8 M concentration of the reactant. The half - life of the reaction is
View SolutionIdentify the order of the reaction from the rate constant value =3.2×10−5Lmol−1s−1.
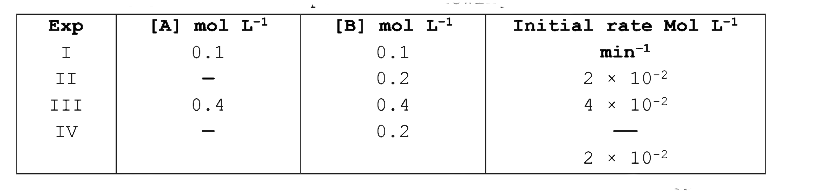
View SolutionThe reaction between A and B is 1st order w.r.t to A and zero order w.r.t B. Find the value of [A] and rate as per the following blanks
View SolutionIdentify the reaction order from each of the following rate :
k=2.3×105Lmol−1s−1
View SolutionIdentify the reaction order from each of the following rate :
k=2.3×105Lmol−1s−1
View Solution