The hydrolyiss of methyl acetate in aqueous solution is has been studied by titrating the liberated acetic acid against NaOH. The concentration of ester at different times is given below:
∣∣∣t (min)0306090C(MolL−1)0.85000.80040.75380.7096∣∣∣
Show that it follows a pseudo first order reaction, as the concentration of water remains nearly constant (55molL−1) during the course of the reaction . What is the value of k' in the equation ?
Rate =k'[CH3COOCH3][H2O]
To show that the hydrolysis of methyl acetate in aqueous solution follows a pseudo first-order reaction and to calculate the value of k′, we will follow these steps:
Step 1: Understand the Reaction
The hydrolysis of methyl acetate can be represented as:
CH3COOCH3+H2O→CH3COOH+CH3OH
In this reaction, methyl acetate reacts with water to produce acetic acid and methanol.
Step 2: Identify the Rate Law
The rate of the reaction can be expressed as:
Rate=k(CH3COOCH3)(H2O)
Since the concentration of water remains nearly constant (approximately 55mol L−1), we can treat it as a constant. Thus, we can define a new rate constant k′:
k′=k(H2O)
This allows us to express the rate as:
Rate=k′(CH3COOCH3)
indicating that the reaction behaves as a pseudo first-order reaction with respect to methyl acetate.
Step 3: Calculate k′ Using Experimental Data
We will use the provided concentration data at different times to calculate k′.
Given data:
- C0=0.8500mol L−1 (initial concentration)
- Concentrations at different times:
- t=30min,C=0.8004
- t=60min,C=0.7538
- t=90min,C=0.7096
Using the first-order kinetics equation:
k=2.303tlog(C0Ct)
For t=30min:
k30=2.30330log(0.85000.8004)≈2.004×10−3min−1
For t=60min:
k60=2.30360log(0.85000.7538)≈2.002×10−3min−1
For t=90min:
k90=2.30390log(0.85000.7096)≈2.005×10−3min−1
Step 4: Average the Rate Constants
Now, we can average the values of k:
kavg=k30+k60+k903≈2.004+2.002+2.0053≈2.004×10−3min−1
Step 5: Calculate k′
Using the average value of k and the concentration of water:
k′=kavg(H2O)=2.004×10−355≈3.64×10−5mol−1Lmin−1
Conclusion
The hydrolysis of methyl acetate is a pseudo first-order reaction, and the value of k′ is approximately 3.64×10−5mol−1Lmin−1.
---
The hydrolysis of methyl acetate can be represented as:
CH3COOCH3+H2O→CH3COOH+CH3OH
In this reaction, methyl acetate reacts with water to produce acetic acid and methanol.
The rate of the reaction can be expressed as:
Rate=k(CH3COOCH3)(H2O)
Since the concentration of water remains nearly constant (approximately 55mol L−1), we can treat it as a constant. Thus, we can define a new rate constant k′:
k′=k(H2O)
This allows us to express the rate as:
Rate=k′(CH3COOCH3)
indicating that the reaction behaves as a pseudo first-order reaction with respect to methyl acetate.
We will use the provided concentration data at different times to calculate k′.
- C0=0.8500mol L−1 (initial concentration)
- Concentrations at different times:
- t=30min,C=0.8004
- t=60min,C=0.7538
- t=90min,C=0.7096
k=2.303tlog(C0Ct)
k30=2.30330log(0.85000.8004)≈2.004×10−3min−1
k60=2.30360log(0.85000.7538)≈2.002×10−3min−1
k90=2.30390log(0.85000.7096)≈2.005×10−3min−1
Now, we can average the values of k:
kavg=k30+k60+k903≈2.004+2.002+2.0053≈2.004×10−3min−1
Using the average value of k and the concentration of water:
k′=kavg(H2O)=2.004×10−355≈3.64×10−5mol−1Lmin−1
The hydrolysis of methyl acetate is a pseudo first-order reaction, and the value of k′ is approximately 3.64×10−5mol−1Lmin−1.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Solved Example
52 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.1 (Objective)
9 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
Hydrolysis of methyl acetate in aqueous solution has been studied by titrating the liberated acetic acid against sodium hydroxide. The concentration of the ester at different times is given below:
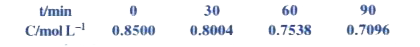
Show that it follows a pseudo first order reaction, as the concentration of water remains nearly constant (55 mol L−1) during the course of the reaction. What is the value of k'in this equation? Rate =k'[CH3COOCH3][H2O]
View SolutionHydrolysis of methyl acetate in aqueous solution has been studied by titrating the liberated acetic acid against sodium hydroxide. The concentration of the ester at different times is given below:
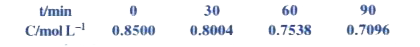
Show that it follows a pseudo first order reaction, as the concentration of water remains nearly constant (55 mol L−1) during the course of the reaction. What is the value of k'in this equation? Rate =k'[CH3COOCH3][H2O]
View Solution
Knowledge Check
In a first order reaction, the concentration of reactant decrease from 400 mol L−1 to 25 mol L−1 in 200 seconds. The rate constant for the reaction is
A1.01386s−1B2×10−4s−1C1.386×10−2s−1D3.4×10−4s−1
Hydrolysis of methyl acetate in aqueous solution has been studied by titrating the liberated acetic acid against sodium hydroxide. The concentration of the ester at different times is given below:
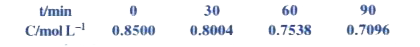
Show that it follows a pseudo first order reaction, as the concentration of water remains nearly constant (55 mol L−1) during the course of the reaction. What is the value of k'in this equation? Rate =k'[CH3COOCH3][H2O]
View SolutionThe half life period for a reaction at initial concentration of 0.2 and 0.4 mol L^(-1) are 100 s and 200 s respectively. The order of the reaction is
View SolutionIn a reaction 2A →Product the concentration of A decreases from 0.8 mole/L to 0.3 mole/L in 20 min. The rate of the reaction during this interval of time is
View SolutionFor a zero order reaction,
K=1×10−3mol L−1s−1
If initial concentration of the reactant is 1.0mol L−1 , the concentration after 10 minutes would be
View SolutionThe half-life periofs of a reaction at initial concentration 0.1molL−1 and 0.5molL−1 are 200s and 40s, respectively. The order of the reaction is
View SolutionThe rate of a first order reaction is 1.5×10−2molL−1min−1 at 0.8 M concentration of the reactant. The half - life of the reaction is
View SolutionThe specific rate constant for a first order reaction is 60×10−4sec−1. If the initial concentration of the reactant is 0.01molL−1, the rate is
View Solution
