The following data were reported for the decompoistion of N2O5 in CCl4 at 303K:
∣∣∣Time (min)120160200240∞Vol ofO2(mL)37.7045.8552.6758.3484.35∣∣∣
Show that the reaction is the first order and calculate the rate constant.
Note: This is an example of direct-estimation of Product, i.e., O2.
To demonstrate that the decomposition of N2O5 in CCl4 is a first-order reaction and to calculate the rate constant, we will follow these steps:
Step 1: Understand the Reaction
The decomposition of N2O5 produces O2 and NO2. The reaction can be represented as:
N2O5→NO2+O2
Step 2: Gather the Data
We have the following data for the volume of O2 produced at different times:
| Time (min) | Volume of O2 (mL) |
|------------|---------------------------|
| 120 | 37.70 |
| 160 | 45.85 |
| 200 | 52.67 |
| 240 | 58.34 |
| ∞ | 84.35 |
Step 3: Use the First-Order Kinetics Equation
For a first-order reaction, the relationship between time and concentration (or volume of product) is given by:
t=2.303klog(V∞V∞−Vt)
Where:
- t = time
- k = rate constant
- V∞ = final volume of O2 at completion of reaction
- Vt = volume of O2 at time t
Step 4: Calculate the Rate Constant k
We will calculate k for each time point using the above equation.
1. For t=120 min:
k=2.303120log(84.3584.35−37.70)
k=2.303120log(84.3546.65)
k≈0.0049min−1
2. For t=160 min:
k=2.303160log(84.3584.35−45.85)
k=2.303160log(84.3538.50)
k≈0.0049min−1
3. For t=200 min:
k=2.303200log(84.3584.35−52.67)
k=2.303200log(84.3531.68)
k≈0.0049min−1
4. For t=240 min:
k=2.303240log(84.3584.35−58.34)
k=2.303240log(84.3526.01)
k≈0.0049min−1
Step 5: Conclusion
Since the rate constant k remains constant (approximately 0.0049min−1) across all time points, we conclude that the reaction is indeed first-order with respect to N2O5.
The decomposition of N2O5 produces O2 and NO2. The reaction can be represented as:
N2O5→NO2+O2
We have the following data for the volume of O2 produced at different times:
|------------|---------------------------|
| 120 | 37.70 |
| 160 | 45.85 |
| 200 | 52.67 |
| 240 | 58.34 |
| ∞ | 84.35 |
For a first-order reaction, the relationship between time and concentration (or volume of product) is given by:
t=2.303klog(V∞V∞−Vt)
Where:
- t = time
- k = rate constant
- V∞ = final volume of O2 at completion of reaction
- Vt = volume of O2 at time t
We will calculate k for each time point using the above equation.
k=2.303120log(84.3584.35−37.70)
k=2.303120log(84.3546.65)
k≈0.0049min−1
k=2.303160log(84.3584.35−45.85)
k=2.303160log(84.3538.50)
k≈0.0049min−1
k=2.303200log(84.3584.35−52.67)
k=2.303200log(84.3531.68)
k≈0.0049min−1
k=2.303240log(84.3584.35−58.34)
k=2.303240log(84.3526.01)
k≈0.0049min−1
Since the rate constant k remains constant (approximately 0.0049min−1) across all time points, we conclude that the reaction is indeed first-order with respect to N2O5.
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Solved Example52videos
CHEMICAL KINETICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.1 (Objective)9videos
CHEMICAL KINETICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)34videos
CARBOXYLIC ACIDS AND THEIR DERIVATIVES
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective18videos
COORDINATION COMPOUNDS
Similar Questions
In an experiment on the decomposition of an aqueous NH4NO2 at a certain temperature, the volume of nitrogen gas collected at different intervals of time was as follows:
∣∣∣Time (s)11902300∞Vol ofN2(mL)5.007.309.50∣∣∣
Show how the above data illustrate that the reaction is of first order.
Note: This is an example of direct-estimation of Product, i.e., N2.View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
 View Solution
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
 View Solution
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
 View Solution
View Solutionform the following data for the decompoistion of N2O5 in carbon tertrachloride solution at 321K, show that the reaction is of the first order and calculate the rate constant.
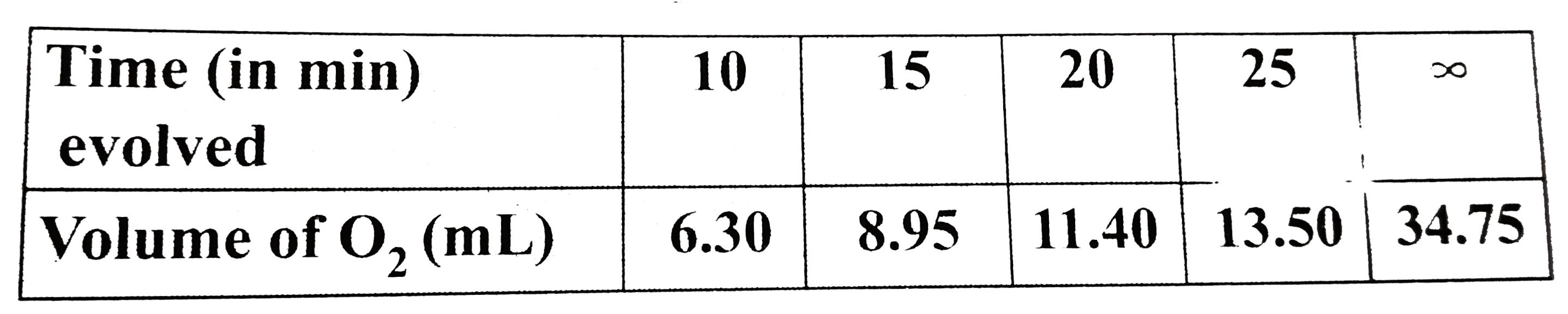 View Solution
View SolutionThe following results were obtained in the decomposition of N2O5 in CCl4 at 315 K:

where x denotes the volume of oxygen evolved in seconds. Show that reaction is of first order and also calculate the rate constant.View SolutionThe following results were obtained in the decomposition of N2O5 in CCl4 at 315 K:

where x denotes the volume of oxygen evolved in seconds. Show that reaction is of first order and also calculate the rate constant.View SolutionThe following results were obtained in the decomposition of N2O5 in CCl4 at 315 K:

where x denotes the volume of oxygen evolved in seconds. Show that reaction is of first order and also calculate the rate constant.View SolutionFollowing data were obtained during the thermal decompoistion of sulphuryl chloride at constant volume and 285∘C.
SO2Cl2(g)→SO2+Cl2(g)
∣∣∣Time (s)0240600Pressure (torr)180244302∣∣∣
Show that it is first order reaction.View SolutionThe following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣ ∣ ∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣ ∣ ∣∣
Calculate the rate constant.View Solution

