In a catalyst experiment involving the Haber process N2+3H2→2NH3, the rate of reaction was measured as
Rate =Δ[NH3]Δt=2.0×10−4molL−1s−1
What is the rate of reaction expressed in terms of (a) N2 (b) H2 ?
2.50×10−4molL−1s−1
1.25×10−4molL−1s−1
3.75×10−4molL−1s−1
5.00×10−4molL−1s−1
The correct Answer is:C
To solve the problem, we need to express the rate of reaction in terms of the reactants N2 and H2 based on the given rate of formation of NH3.
1. Write the balanced chemical equation:
N2+3H2→2NH3
2. Identify the relationship between the rates of change of the reactants and products:
According to the stoichiometry of the reaction:
- The rate of consumption of N2 is half the rate of formation of NH3.
- The rate of consumption of H2 is one and a half times the rate of formation of NH3.
Mathematically, this can be expressed as:
−d(N2)dt=12d(NH3)dt
−d(H2)dt=13d(NH3)dt
3. Given rate of formation of NH3:
d(NH3)dt=2.0×10−4mol L−1s−1
4. Calculate the rate of reaction in terms of N2:
Using the relationship for N2:
−d(N2)dt=12d(NH3)dt
Substitute the given rate:
−d(N2)dt=12×(2.0×10−4)=1.0×10−4mol L−1s−1
5. Calculate the rate of reaction in terms of H2:
Using the relationship for H2:
−d(H2)dt=13d(NH3)dt
Substitute the given rate:
−d(H2)dt=13×(2.0×10−4)=2.0×10−43=2.03×10−4≈6.67×10−5mol L−1s−1
Final Answers:
- (a) Rate of reaction in terms of N2: 1.0×10−4mol L−1s−1
- (b) Rate of reaction in terms of H2: 6.67×10−5mol L−1s−1
N2+3H2→2NH3
According to the stoichiometry of the reaction:
- The rate of consumption of N2 is half the rate of formation of NH3.
- The rate of consumption of H2 is one and a half times the rate of formation of NH3.
−d(N2)dt=12d(NH3)dt
−d(H2)dt=13d(NH3)dt
d(NH3)dt=2.0×10−4mol L−1s−1
Using the relationship for N2:
−d(N2)dt=12d(NH3)dt
Substitute the given rate:
−d(N2)dt=12×(2.0×10−4)=1.0×10−4mol L−1s−1
Using the relationship for H2:
−d(H2)dt=13d(NH3)dt
Substitute the given rate:
−d(H2)dt=13×(2.0×10−4)=2.0×10−43=2.03×10−4≈6.67×10−5mol L−1s−1
- (a) Rate of reaction in terms of N2: 1.0×10−4mol L−1s−1
- (b) Rate of reaction in terms of H2: 6.67×10−5mol L−1s−1
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Assertion-Reasoning
22 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Integer
15 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Multiple Correct
33 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
In the hober's process of ammonia manufacture,
N2(g)+3H2(g)→2NH3(g)
the rate of appearance of NH3 is :
d[NH3]dt=2×10−4molL−1sec−1
The rates of the reaction expressed in terms of N2andH2 will be :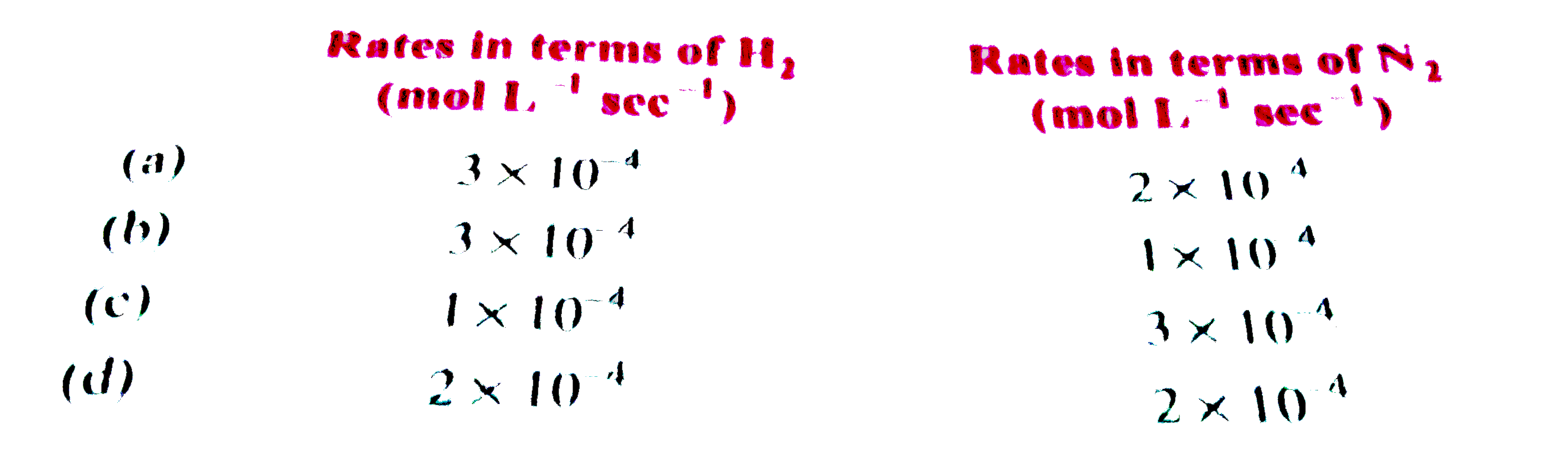
View SolutionFor a reaction , 2A+D→3C, the rate of appearance of C at time t is 1.2×10−4mol L−1s−1 . Find the rate of reaction.
View Solution
Knowledge Check
For the reaction 4NH3+5O2→4NO+6H2O, if the rate of disappearance of NH3 is 3.6×10−3 mol L−1s−1, what is the rate of formation of H2O
A5.4×10−3molL−1s−1B3.6×10−3molL−1s−1C4×10−4molL−1s−1D0.6×10−4molL−1s−1In the reaction N2+3H2→2NH3, the volume ratio of the gases as 1: 3: 2 was
ABoyleBGay-Lussac's lawCAvogadroDCharlesConsider the reaction, 2N2O5→4NO2+O2 In the reaction NO2 is being formed at the rate of 0.0125 mol L−1s−1. What is the rate of reaction at this time?
A0.0018 mol L−1s−1B0.0031 mol L−1s−1C0.0041 mol L−1s−1D0.050 mol L−1s−1
For the reaction N2+3H2→2NH3 if
Δ[NH3]Δt=2×10−4molL−1s−1, the value of −Δ[H2]Δt would be
View SolutionIn a catalytic conversion of N2 to NH3 by Haber's process, the rate of reaction was expressed as change in the concentration of ammonia per time is 40×10−3molL−1s−1. If there are no side reaction, the rate of the reaction as expressed in terms of hydrogen is (in mol L−1s−1)
View SolutionFor the reaction
H2(g)+I2(g)→2HI(g), the rate of disappearance of H2 is 1.0×10−4molL−1s−1. The rate of appearance of HI will be
View SolutionFor the reaction N2(g)+3H2(g)→2NH3(g) if Δ[NH3]Δt=4×10−4mol.l−1s−1, the value of −Δ[H2]Δt would be
View SolutionFor the reaction N2+3H2→2NH3, if d[NH3]dt.=4×10−4 mol L−1s−1, the value of −d[H2]dt would be
View Solution
