Derive the following:
a. Langmuir iostherm
b. Freundlich iostherm
Step-by-Step Derivation of Langmuir and Freundlich Isotherms
A. Derivation of Langmuir Isotherm
1. Assumptions of Langmuir Isotherm:
- The adsorption occurs only on a surface that has a finite number of identical sites.
- Each site can hold only one molecule (unimolecular layer).
- There is no interaction between adsorbed molecules.
- The process is reversible.
2. Rate of Adsorption:
- The rate of adsorption (R_a) is proportional to the pressure of the gas (P) and the fraction of unoccupied sites (1 - θ):
Ra=ka⋅P⋅(1−θ)
where ka is the rate constant for adsorption and θ is the fraction of the surface covered by the adsorbate.
3. Rate of Desorption:
- The rate of desorption (R_d) is proportional to the fraction of occupied sites (θ):
Rd=kd⋅θ
where kd is the rate constant for desorption.
4. Equilibrium Condition:
- At equilibrium, the rate of adsorption equals the rate of desorption:
Ra=Rd
Thus, we can write:
ka⋅P⋅(1−θ)=kd⋅θ
5. Rearranging the Equation:
- Rearranging gives:
ka⋅P−ka⋅P⋅θ=kd⋅θ
- Collecting terms involving θ:
ka⋅P=θ⋅(ka⋅P+kd)
6. Solving for θ:
- Rearranging to solve for θ:
θ=ka⋅Pka⋅P+kd
- Let K=kakd (equilibrium constant):
θ=K⋅P1+K⋅P
7. Final Form of Langmuir Isotherm:
- The Langmuir isotherm can be expressed as:
θ=K⋅P1+K⋅P
B. Derivation of Freundlich Isotherm
1. Assumptions of Freundlich Isotherm:
- The Freundlich isotherm is applicable for physical adsorption.
- It assumes a heterogeneous surface with sites of varying energies.
2. Freundlich Adsorption Equation:
- The Freundlich isotherm can be expressed as:
xm=k⋅P1n
where xm is the amount of gas adsorbed per unit mass of adsorbent, k is a constant, and n is a constant that indicates the degree of non-linearity.
3. Taking Logarithms:
- Taking logarithms on both sides gives:
log(xm)=log(k)+1nlog(P)
4. Graphical Representation:
- This equation is in the form of y=mx+c, where:
- y=log(xm)
- x=log(P)
- m=1n (slope)
- c=log(k) (y-intercept)
5. Behavior at Different Pressures:
- At low pressure, 1n approaches 1, and xm is directly proportional to P.
- At high pressure, 1n approaches 0, indicating saturation where xm becomes constant.
- The adsorption occurs only on a surface that has a finite number of identical sites.
- Each site can hold only one molecule (unimolecular layer).
- There is no interaction between adsorbed molecules.
- The process is reversible.
- The rate of adsorption (R_a) is proportional to the pressure of the gas (P) and the fraction of unoccupied sites (1 - θ):
Ra=ka⋅P⋅(1−θ)
where ka is the rate constant for adsorption and θ is the fraction of the surface covered by the adsorbate.
- The rate of desorption (R_d) is proportional to the fraction of occupied sites (θ):
Rd=kd⋅θ
where kd is the rate constant for desorption.
- At equilibrium, the rate of adsorption equals the rate of desorption:
Ra=Rd
Thus, we can write:
ka⋅P⋅(1−θ)=kd⋅θ
- Rearranging gives:
ka⋅P−ka⋅P⋅θ=kd⋅θ
- Collecting terms involving θ:
ka⋅P=θ⋅(ka⋅P+kd)
- Rearranging to solve for θ:
θ=ka⋅Pka⋅P+kd
- Let K=kakd (equilibrium constant):
θ=K⋅P1+K⋅P
- The Langmuir isotherm can be expressed as:
θ=K⋅P1+K⋅P
- The Freundlich isotherm is applicable for physical adsorption.
- It assumes a heterogeneous surface with sites of varying energies.
- The Freundlich isotherm can be expressed as:
xm=k⋅P1n
where xm is the amount of gas adsorbed per unit mass of adsorbent, k is a constant, and n is a constant that indicates the degree of non-linearity.
- Taking logarithms on both sides gives:
log(xm)=log(k)+1nlog(P)
- This equation is in the form of y=mx+c, where:
- y=log(xm)
- x=log(P)
- m=1n (slope)
- c=log(k) (y-intercept)
- At low pressure, 1n approaches 1, and xm is directly proportional to P.
- At high pressure, 1n approaches 0, indicating saturation where xm becomes constant.
Topper's Solved these Questions
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Ex 5.2
11 Videos
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Exercises Subjective
10 Videos
- SURFACE CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Solved Examples
20 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
- SYNTHETIC AND NATURAL POLYMERSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SYNTHETIC AND NATURAL POLYMERSEXERCISE - Exercises Assertion Reasoning
10 Videos
Similar Questions
Knowledge Check
Which of the following curves is in accordance with Freundlich adsorption isotherm ?
A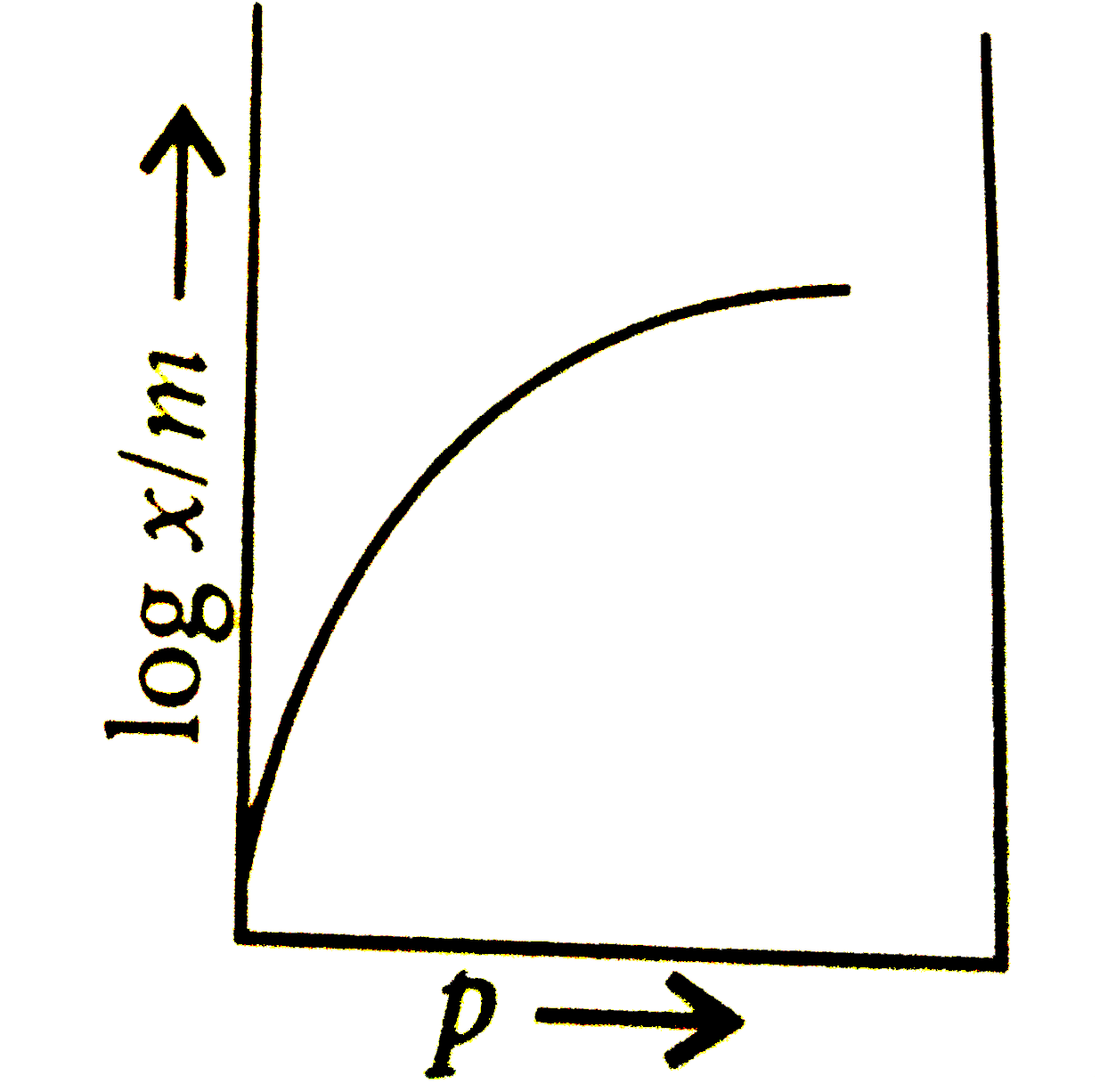 B
B C
C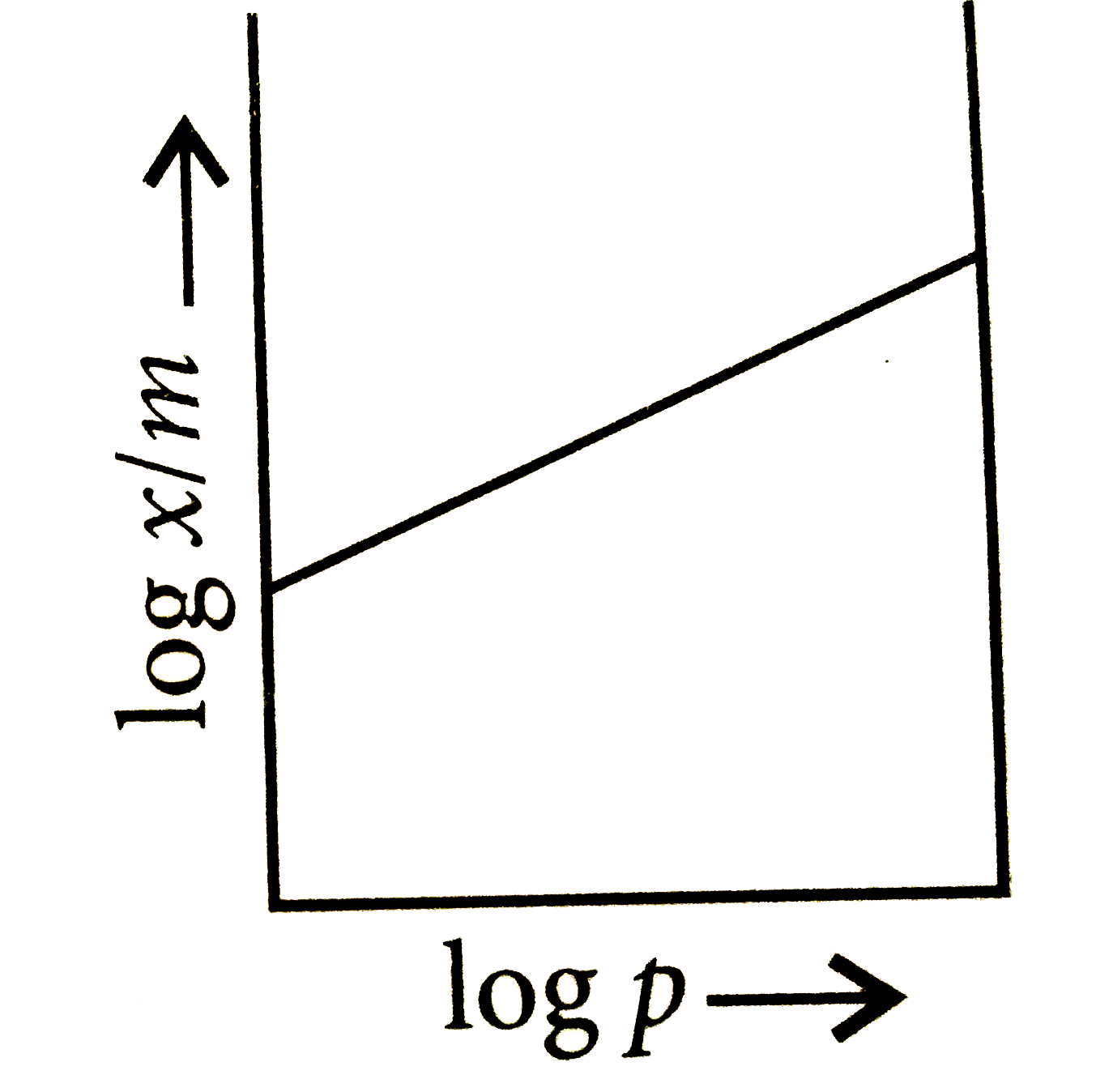 D
D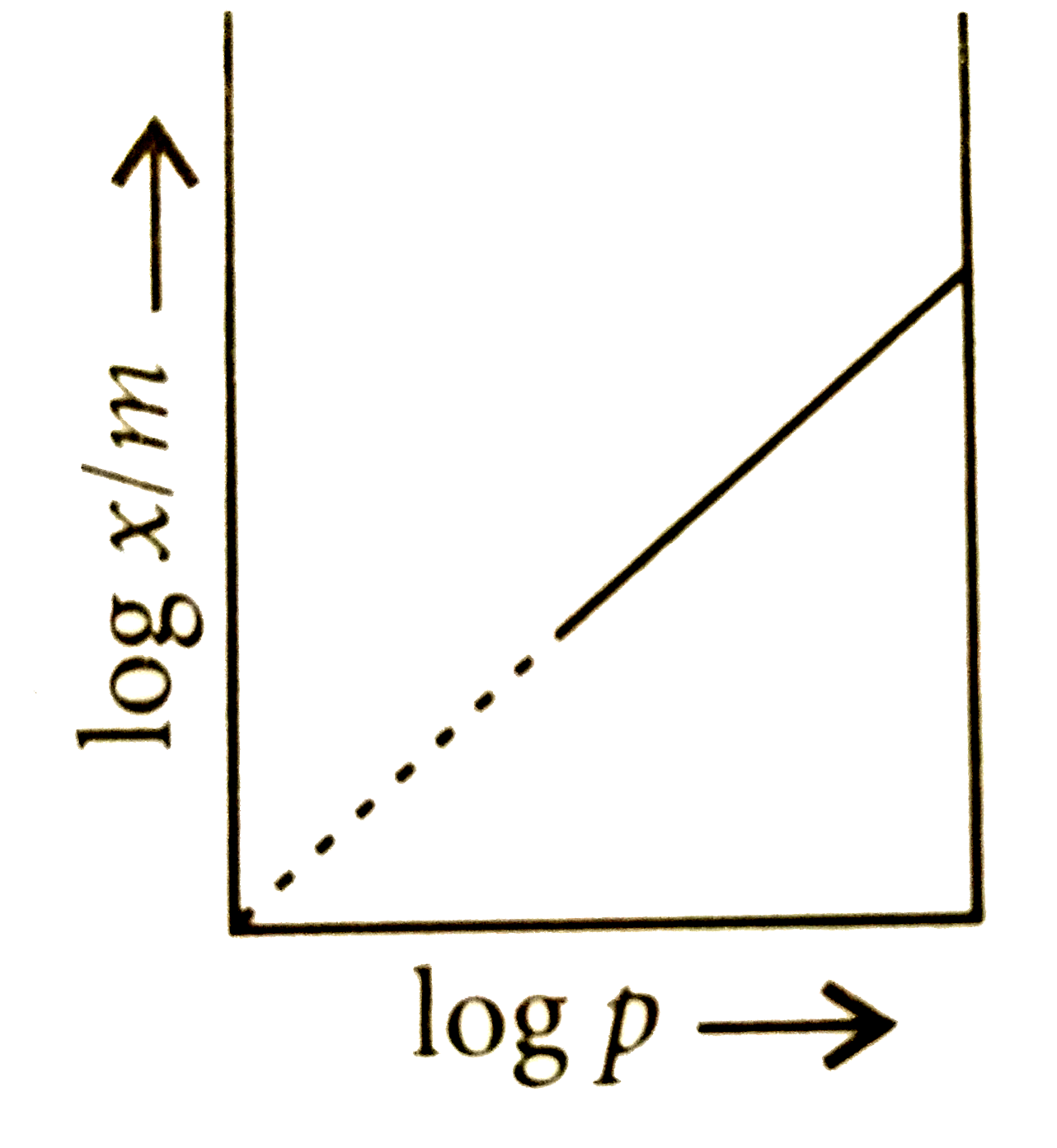
Which one of the following is not a derived unit?
AJouleBwattCKilogramDnewton
Which of the following curves is in according with Freundlich adsorption isotherm?
(a)
(b)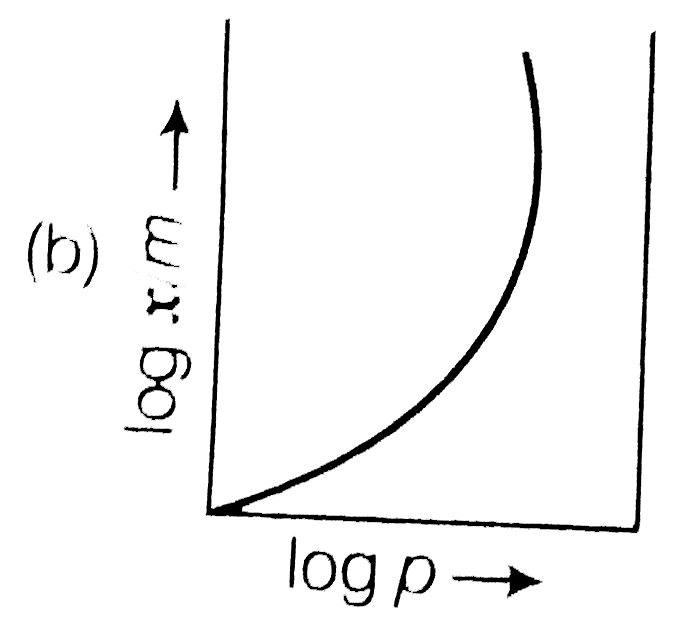
(c)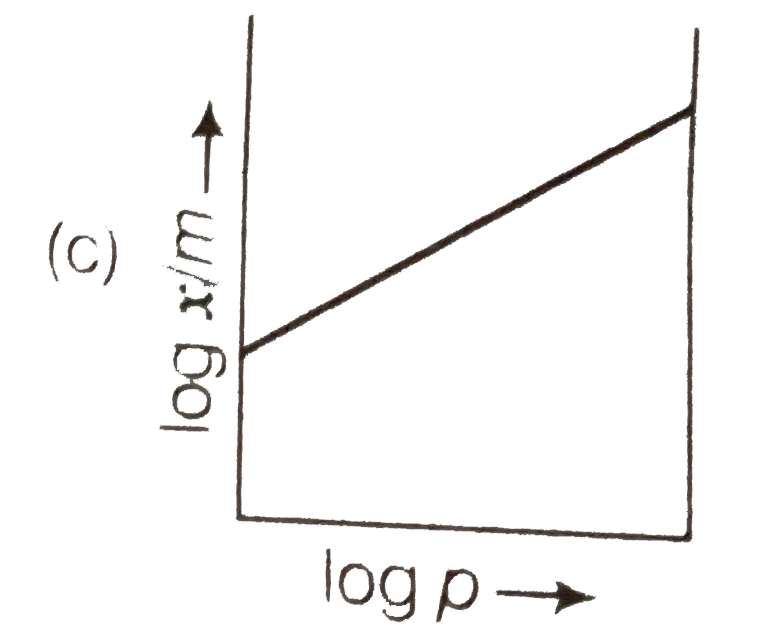
(d)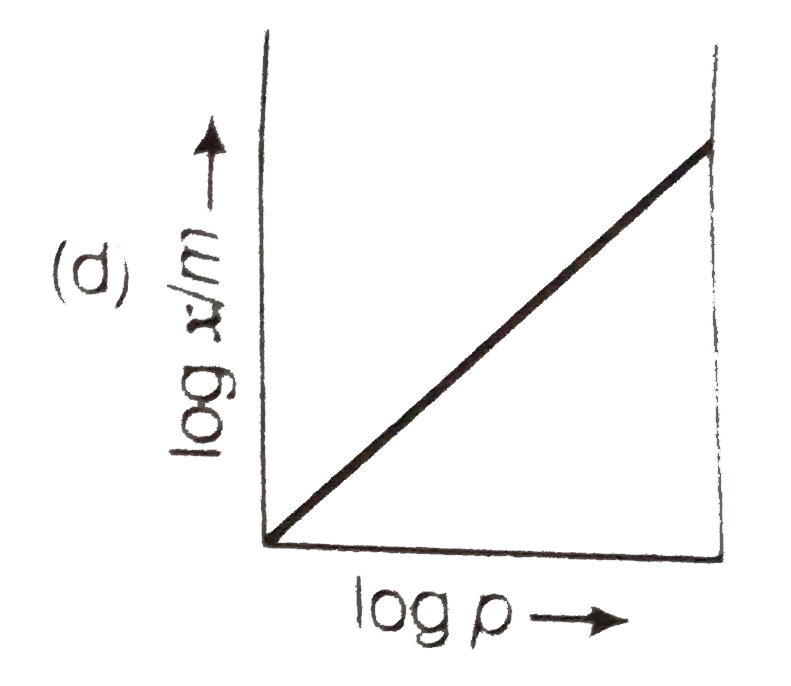
View SolutionWhich of the following graphs represents freundlich adsorption isotherm?
View SolutionIf x/m is the mass of adsorbate adsorbed per unit mass of adsorbent, P is the pressure of the adsorbate gas ,a and b are constant ,which of the following represent "Langmuir adsorption isotherm"?
View SolutionA gas undergoes physical adsorption on a surface and follows the givn Freundlich adsoprtion isotherm equation xm=kp0.5. Adsorption of the gas increases with:
View SolutionA gas undergoes physical adsorption on a surface and follows the givn Freundlich adsoprtion isotherm equation xm=kp0.5. Adsorption of the gas increases with:
View SolutionWhich of the following is a derived lipid ?
View Solution
