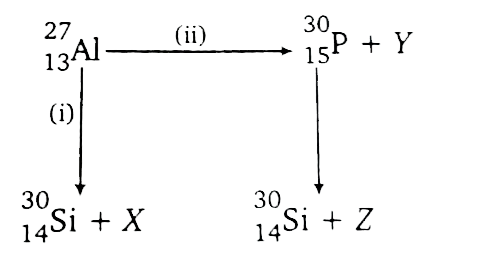
Bombardment of aluminium of α− particle leads to its artificial disintegration in two ways (i) and (ii) as shown below. Product X,Y, and Z, respectively, are
.14Si30+X(i)←−−.13Al27(ii)−−→.15P30+Y→.14Si30+Z
Proton, neutron, positron
Neutron, positron, proton
Proton, positron, neutron
Positron, proton, neutron
The correct Answer is:A
To solve the problem of the bombardment of aluminum with alpha particles leading to artificial disintegration, we will analyze the reactions step by step.
Step 1: Analyze the first reaction
The first reaction is:
2713Al+α→3014Si+X
where α represents the alpha particle, which has a mass number of 4 and an atomic number of 2.
Mass Number Calculation:
- Mass number on the left side (reactants):
27+4=31
- Mass number on the right side (products):
30+mass number of X
- Setting the two sides equal:
31=30+mass number of X
- Solving for the mass number of X:
mass number of X=31−30=1
Atomic Number Calculation:
- Atomic number on the left side (reactants):
13+2=15
- Atomic number on the right side (products):
14+atomic number of X
- Setting the two sides equal:
15=14+atomic number of X
- Solving for the atomic number of X:
atomic number of X=15−14=1
Since X has a mass number of 1 and an atomic number of 1, it is identified as a proton (p).
Step 2: Analyze the second reaction
The second reaction is:
2713Al+α→3015P+Y
Mass Number Calculation:
- Mass number on the left side (reactants):
27+4=31
- Mass number on the right side (products):
30+mass number of Y
- Setting the two sides equal:
31=30+mass number of Y
- Solving for the mass number of Y:
mass number of Y=31−30=1
Atomic Number Calculation:
- Atomic number on the left side (reactants):
13+2=15
- Atomic number on the right side (products):
15+atomic number of Y
- Setting the two sides equal:
15=15+atomic number of Y
- Solving for the atomic number of Y:
atomic number of Y=15−15=0
Since Y has a mass number of 1 and an atomic number of 0, it is identified as a neutron (n).
Step 3: Analyze the third reaction
The third reaction is:
3015P→3014Si+Z
Mass Number Calculation:
- Mass number on the left side (reactants):
30
- Mass number on the right side (products):
30+mass number of Z
- Setting the two sides equal:
30=30+mass number of Z
- Solving for the mass number of Z:
mass number of Z=30−30=0
Atomic Number Calculation:
- Atomic number on the left side (reactants):
15
- Atomic number on the right side (products):
14+atomic number of Z
- Setting the two sides equal:
15=14+atomic number of Z
- Solving for the atomic number of Z:
atomic number of Z=15−14=1
Since Z has a mass number of 0 and an atomic number of 1, it is identified as a positron (e+).
Summary of Products
- X is a proton (p)
- Y is a neutron (n)
- Z is a positron (e+)
The first reaction is:
2713Al+α→3014Si+X
where α represents the alpha particle, which has a mass number of 4 and an atomic number of 2.
- Mass number on the left side (reactants):
27+4=31
- Mass number on the right side (products):
30+mass number of X
- Setting the two sides equal:
31=30+mass number of X
- Solving for the mass number of X:
mass number of X=31−30=1
- Atomic number on the left side (reactants):
13+2=15
- Atomic number on the right side (products):
14+atomic number of X
- Setting the two sides equal:
15=14+atomic number of X
- Solving for the atomic number of X:
atomic number of X=15−14=1
The second reaction is:
2713Al+α→3015P+Y
- Mass number on the left side (reactants):
27+4=31
- Mass number on the right side (products):
30+mass number of Y
- Setting the two sides equal:
31=30+mass number of Y
- Solving for the mass number of Y:
mass number of Y=31−30=1
- Atomic number on the left side (reactants):
13+2=15
- Atomic number on the right side (products):
15+atomic number of Y
- Setting the two sides equal:
15=15+atomic number of Y
- Solving for the atomic number of Y:
atomic number of Y=15−15=0
The third reaction is:
3015P→3014Si+Z
- Mass number on the left side (reactants):
30
- Mass number on the right side (products):
30+mass number of Z
- Setting the two sides equal:
30=30+mass number of Z
- Solving for the mass number of Z:
mass number of Z=30−30=0
- Atomic number on the left side (reactants):
15
- Atomic number on the right side (products):
14+atomic number of Z
- Setting the two sides equal:
15=14+atomic number of Z
- Solving for the atomic number of Z:
atomic number of Z=15−14=1
- X is a proton (p)
- Y is a neutron (n)
- Z is a positron (e+)
Topper's Solved these Questions
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Archives Assertion-Reasoning
2 Videos
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Archives Integer-Type
1 Videos
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Archives Multiple Correct
3 Videos
- NCERT BASED EXERCISEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - Nuclear Chemistry (NCERT Exercise)
29 Videos
- ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPEXERCISE - Archives Analytical And Descriptive
24 Videos
Similar Questions
Bombardment of aluminium by α−particle leads to its artificial disintegration in two ways, (i)and(ii) as shown.
Products X,Y and Z respectively, are
View SolutionBombardment by α-particle leads to artificial distintegration in three ways, (I) , (II) and (III) as shown . Products X , Y and Z respectively are :
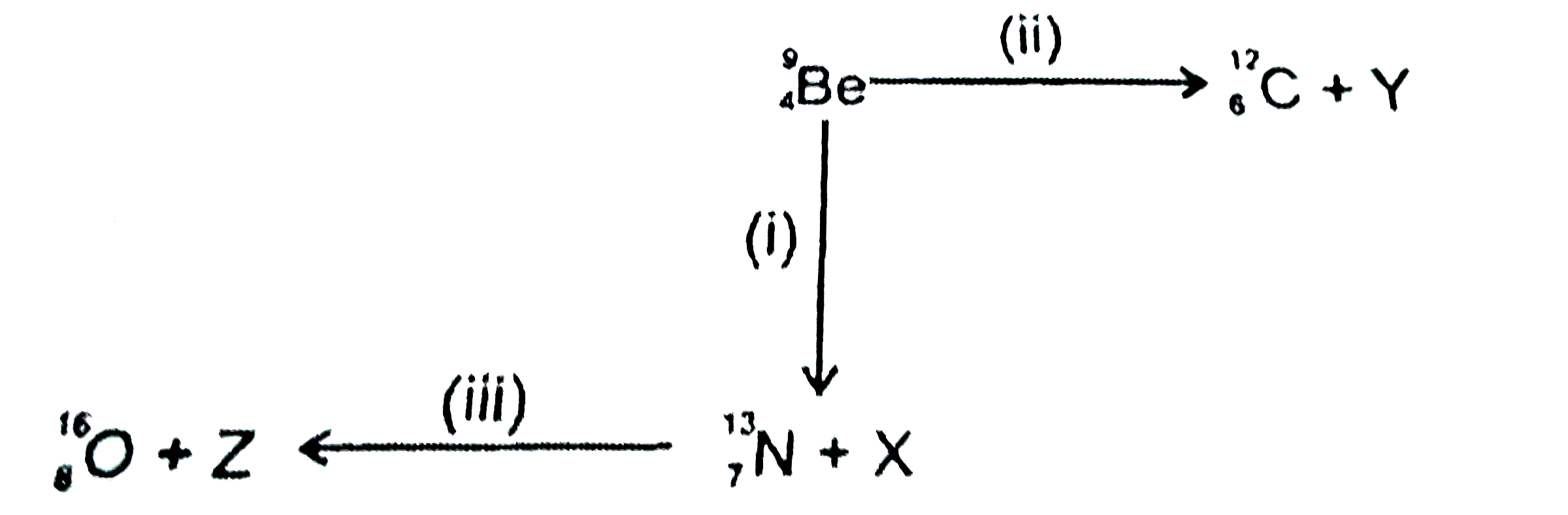
View SolutionWhich of the following particles is emitted in the nuclear reaction: .13Al27+.2He4→.14P30+….?
View SolutionWhat is (Z) is the following sequence of reaction?
HC≡CH(i)2NaNH2(ii)2CH3I−−−−−−−−−−−−−−→(X)HgSO4,H2SO4−−−−−−−−→(Y)(i)NaOH+Br3(ii)H3O+−−−−−−−−−−−−−−−−→(Z)
View SolutionA square platform of side length 8m is is situated in x−z plane sucha that it is at 16m form the x-axis and 8m from the z-axis as shown in figure. A particle is projected with velocity →v=(v2^i+25ˆj)m/s relative to wind form origin and at the same instant the platform starts with acceleration →=(2ˆi+2.5ˆj)m/s2. Wind is blowing with velocity v1ˆk.g=10m/s2
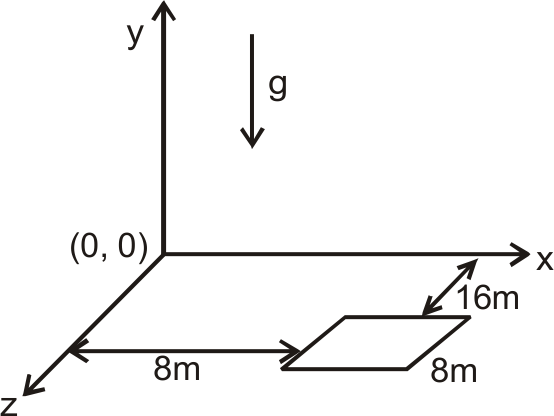
ListIList II(P)Least possible values of V2(in M/s) so that particle hits the platform or edge of platfrom is(1)4(Q)Least possible values of v1(in m/s) so that particle hits the platform or edge or platform is (2)6(Q)If t is the time (in seconds) after particle hits the platform then 2t is equal to (3)8(S)Value of displacement with respect to ground (in m) of the particle in y-direction , when v2 has its minimum possible value is (till particle hits the platform or edge of platform)(4)20
View SolutionEstimation of nitrogen: There are two methods for the estimation of nitrogen (i) Dumas method and (ii) Kjedahl's method.
i. Dumas method: A known mass of compound is heated with copper oxide (CuO) in an atomsphere of CO2, which gives free nitrogen along with CO2andH2O
CxHyNz+(2x+y/2)CuO→xCO2+y/2(H2O)+z/2(N2)+(2x+y/2)CU
The gaseous mixture is passed over a heated copper gauze which converts traces of nitrogen oxides formed to N2. The gaeous mixture is collected over an aqueous solution of KOH which absorbs CO2, and nitrogen is callected in the upper part of the graduated tube.
ii. Kjeldahl's method: A known mass of organic compound (0.5 gm) is mixed with K2SO4 (10 gm) and CuSO4. (1.0 gm) or a drop of mercury (Hg) and conc. H2SO4 (25ml), and heated in Kjeldahl's flask. CuSO4 or Hg acts as a catalyst, while K2SO4 raises the boiling point of H2SO4. The nitrogen in the organic compound is quantitatively converted to ammonium sulphate. The resulting mixture is then distilled with excess of NaOH solution and the NH3 evolved is passed into a known but excess volume of standard HCl or H2SO4. The acid left unused is estimated by titration with some standard alkali. The amount of acid used against NH3 can be thus be known and from this the percentage of nitrogen is calculated.
(a) C+H+Sconc.−−−→H2SO4CO2+H2O+SO2
(b) Nconc.−−−→H2SO4(NH4)2SO4
(c) (NH4)2SO4+2NaOH→Na2SO4+2NH3+2H2O
(d) 2NH3+H2SO4→(NH4)2SO4
(iii) This method is not applicable to compounds containing N in intro and azo groups, and N present in the ring (e.g., pyridine) as N of these compounds does not change to (NH4)2SO4 (ammonium sulphate) under these reaction conditions
0.50 gm of an organic compound was treated according to Kjeldahl's method. The ammonia evolved was absorbed in 50ml of 0,5M H2SO4. The residual acid required 60 ml of M/2 NaOH solution. Find the percentage of nitrogen in the compound
View SolutionEstimation of nitrogen: There are two methods for the estimation of nitrogen (i) Dumas method and (ii) Kjedahl's method.
i. Dumas method: A known mass of compound is heated with copper oxide (CuO) in an atomsphere of CO2, which gives free nitrogen along with CO2andH2O
CxHyNz+(2x+y/2)CuO→xCO2+y/2(H2O)+z/2(N2)+(2x+y/2)CU
The gaseous mixture is passed over a heated copper gauze which converts traces of nitrogen oxides formed to N2. The gaeous mixture is collected over an aqueous solution of KOH which absorbs CO2, and nitrogen is callected in the upper part of the graduated tube.
ii. Kjeldahl's method: A known mass of organic compound (0.5 gm) is mixed with K2SO4 (10 gm) and CuSO4. (1.0 gm) or a drop of mercury (Hg) and conc. H2SO4 (25ml), and heated in Kjeldahl's flask. CuSO4 or Hg acts as a catalyst, while K2SO4 raises the boiling point of H2SO4. The nitrogen in the organic compound is quantitatively converted to ammonium sulphate. The resulting mixture is then distilled with excess of NaOH solution and the NH3 evolved is passed into a known but excess volume of standard HCl or H2SO4. The acid left unused is estimated by titration with some standard alkali. The amount of acid used against NH3 can be thus be known and from this the percentage of nitrogen is calculated.
(a) C+H+Sconc.−−−→H2SO4CO2+H2O+SO2
(b) Nconc.−−−→H2SO4(NH4)2SO4
(c) (NH4)2SO4+2NaOH→Na2SO4+2NH3+2H2O
(d) 2NH3+H2SO4→(NH4)2SO4
(iii) This method is not applicable to compounds containing N in intro and azo groups, and N present in the ring (e.g., pyridine) as N of these compounds does not change to (NH4)2SO4 (ammonium sulphate) under these reaction conditions
0.4gm of an organic compound was treated according to Kjeldahl's method. The ammonia evolved was absorbed in 50ml of 0.5M H3PO3. The residual acid required 30 ml of 0.5M Ca(OH)2. Find the percentage of N2 in the compound
View SolutionEstimation of nitrogen: There are two methods for the estimation of nitrogen (i) Dumas method and (ii) Kjedahl's method.
i. Dumas method: A known mass of compound is heated with copper oxide (CuO) in an atomsphere of CO2, which gives free nitrogen along with CO2andH2O
CxHyNz+(2x+y/2)CuO→xCO2+y/2(H2O)+z/2(N2)+(2x+y/2)CU
The gaseous mixture is passed over a heated copper gauze which converts traces of nitrogen oxides formed to N2. The gaeous mixture is collected over an aqueous solution of KOH which absorbs CO2, and nitrogen is callected in the upper part of the graduated tube.
ii. Kjeldahl's method: A known mass of organic compound (0.5 gm) is mixed with K2SO4 (10 gm) and CuSO4. (1.0 gm) or a drop of mercury (Hg) and conc. H2SO4 (25ml), and heated in Kjeldahl's flask. CuSO4 or Hg acts as a catalyst, while K2SO4 raises the boiling point of H2SO4. The nitrogen in the organic compound is quantitatively converted to ammonium sulphate. The resulting mixture is then distilled with excess of NaOH solution and the NH3 evolved is passed into a known but excess volume of standard HCl or H2SO4. The acid left unused is estimated by titration with some standard alkali. The amount of acid used against NH3 can be thus be known and from this the percentage of nitrogen is calculated.
(a) C+H+Sconc.−−−→H2SO4CO2+H2O+SO2
(b) Nconc.−−−→H2SO4(NH4)2SO4
(c) (NH4)2SO4+2NaOH→Na2SO4+2NH3+2H2O
(d) 2NH3+H2SO4→(NH4)2SO4
(iii) This method is not applicable to compounds containing N in intro and azo groups, and N present in the ring (e.g., pyridine) as N of these compounds does not change to (NH4)2SO4 (ammonium sulphate) under these reaction conditions
0.002 gm of an organic compound was treated according to Kjeldahl's method. 0.2×10−4mol of H2SO4 was required to neutralise NH3. Calculate the percentage of N2
View SolutionIdentify X,Y and Z in the following synsthetic scheme and write their structures
CH3CH2C=CH(i)NaNH2−−−−−−−−−→(ii)CH3CH2BrX
XH2/pd−BaSO4−−−−−−−−−→Yalkaline−−−−→KMnO4Z
View SolutionAn organic compound containing C, H and O gives following observations:
(i) It exists in two isomeric forms (A) and (B).
(ii) 0.108 g of one of the isomers on combustion gave 0.308 g of CO2 and 0.072 g of H2O
(iii) (A) is insoluble in NaOH and NaHCO3 while (B) is soluble in NaOH.
(iv) (A) reacts with Hl to give compound (C ) and (D). (C ) can be separated from (D) by ethanolic AgNO3 solution and (D) is soluble in NaOH.
(v) (B) readily reacts with bromine water to give compound (E) of molecular formula C7H5OBr3
Compound (D)underset((iii)HCl)underset(4-7" atm,"125K)overset((i)NaOH)overset((ii)CO_(2))rarr(X)overset(CH_(3)COCl)rarr(Y)
The product (Y) is
View Solution
