Ac227 has a half− life of 22.0 years with respect to one leading . To Th227 and the other to Fr227. The percentage yields of these two daughter nuclides are 2.0 and 98.0, respectively . What are the decay constants (λ) for each of the separate paths ?
To solve the problem, we need to find the decay constants for the two decay paths of Ac^(227) leading to Th^(227) and Fr^(227).
1. Identify the Given Data:
- Half-life of Ac^(227) = 22.0 years
- Percentage yield to Th^(227) = 2.0%
- Percentage yield to Fr^(227) = 98.0%
2. Calculate the Overall Decay Constant (k):
The decay constant (k) can be calculated using the formula:
k=0.693t1/2
Substituting the half-life:
k=0.69322.0 years≈0.0315 year−1
3. Establish the Relationship Between Decay Constants:
Since the reactions are parallel, the sum of the decay constants for the two pathways equals the overall decay constant:
k1+k2=k
where k1 is the decay constant for the formation of Th^(227) and k2 is for Fr^(227).
4. Use the Yield Ratios to Relate the Decay Constants:
The ratio of the decay constants is equal to the ratio of the yields:
k1k2=2.098.0=149
This implies:
k1=149k2
5. Substitute into the Decay Constant Equation:
Substitute k1 into the equation k1+k2=k:
149k2+k2=k
Combine the terms:
1+4949k2=k
5049k2=k
Solve for k2:
k2=4950k
6. Calculate k2:
Substitute the value of k:
k2=4950×0.0315≈0.0294 year−1
7. Calculate k1:
Use the relationship k1=149k2:
k1=149×0.0294≈0.0006 year−1
Final Results:
- Decay constant for Th^(227) (k1) ≈ 0.0006 year⁻¹
- Decay constant for Fr^(227) (k2) ≈ 0.0294 year⁻¹
- Half-life of Ac^(227) = 22.0 years
- Percentage yield to Th^(227) = 2.0%
- Percentage yield to Fr^(227) = 98.0%
The decay constant (k) can be calculated using the formula:
k=0.693t1/2
Substituting the half-life:
k=0.69322.0 years≈0.0315 year−1
Since the reactions are parallel, the sum of the decay constants for the two pathways equals the overall decay constant:
k1+k2=k
where k1 is the decay constant for the formation of Th^(227) and k2 is for Fr^(227).
The ratio of the decay constants is equal to the ratio of the yields:
k1k2=2.098.0=149
This implies:
k1=149k2
Substitute k1 into the equation k1+k2=k:
149k2+k2=k
Combine the terms:
1+4949k2=k
5049k2=k
Solve for k2:
k2=4950k
Substitute the value of k:
k2=4950×0.0315≈0.0294 year−1
Use the relationship k1=149k2:
k1=149×0.0294≈0.0006 year−1
- Decay constant for Th^(227) (k1) ≈ 0.0006 year⁻¹
- Decay constant for Fr^(227) (k2) ≈ 0.0294 year⁻¹
Topper's Solved these Questions
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - True//False Type
1 Videos
- NCERT BASED EXERCISEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - Nuclear Chemistry (NCERT Exercise)
29 Videos
- ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPEXERCISE - Archives Analytical And Descriptive
24 Videos
Similar Questions
Ac227 has a half-life of 22 years . The decays follows two parallel paths
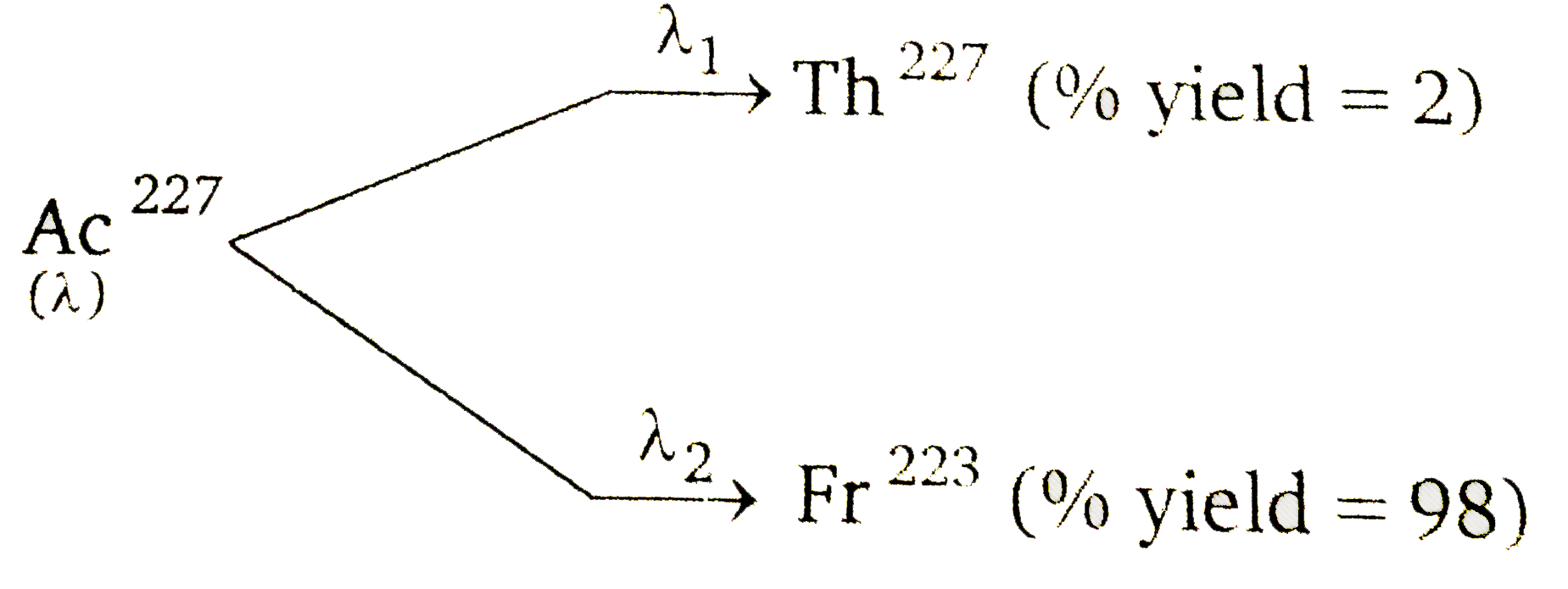
What are the decay constant (λ) for Th and Fr respectively ?
View SolutionThe half-life of 2 sample are 0.1 and 0.4 seconds. Their respctive concentration are 200 and 50 respectively. What is the order of the reaction
View Solution
Knowledge Check
A system consists of two charges 4μCand−3μC with no external field placed at (−5cm,0,0)and(+5cm,0,0) respectively. The amount of work required to separated the two charges infinitely away from each other is
A−1.1JB2JC2.5JD3J
Uranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions
Number of nuclei of B at any time t is
View SolutionUranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=−λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=−λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions ltbgt Numeber of the nuclei of nuclei C at time t is
View SolutionThe dissociation constants of two acids HA1 and HA2 are 3.0×10−4 and 1.8×10−5 respectively. The relative strengths of the acids will be approximately
View SolutionThe escape velocity at the surface of Earth is approximately 8 km/s. What is the escape velocity for a planet whose radius is 4 times and whose mass is 100 times that of Earth?
View SolutionTwo plates of equal area are placed in contact with each other. The thickness of the plates are 2.0 cm and 3.0 cm respectively. The outer face of first plate is at −25∘C and that of second plate is at +25∘C. The conductivities of the plates are in the ratio 2:3. Calculate the temperature of the common surface of the plates.
View SolutionHalf-life of 210Pb is 22 years. 2gram of lead is allowed decay for 11 years. (a) How much lead is left ?and (b) What is the percentage decay ?
View SolutionTwo radioactive materials A & B have decay constant 3λ and 2λ respectively. At t=0 the numbers of nuclei of A and B are 4N0 and 2N0 respectively then,
View Solution
