Question

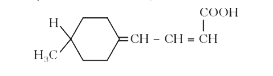
How many stereoisomers are possible for the compound $C{H}_{3}CH=CHCHClC{H}_3$?

Explanation

To determine the number of stereoisomers for the compound $CH₃CH=CHCHClCH₃$, we can follow these steps:

Step 1: Identify the Structure
First, we need to draw the structure of the compound. The given compound can be represented as follows:

```
CH₃
|
CH₃-CH=CH-CHCl
```

Step 2: Identify Stereocenters
Next, we need to identify the stereocenters in the compound. A stereocenter is typically a carbon atom that is bonded to four different groups.

1. Chiral Carbon: In this compound, the carbon atom bonded to the chlorine (Cl) is a chiral center because it is attached to four different substituents:
- CH₃
- H (hydrogen)
- CH=CH (the rest of the carbon chain)
- Cl

2. Double Bond: The double bond between the second and third carbon atoms (C=C) can also contribute to stereoisomerism. This double bond can have two configurations (cis and trans).

Step 3: Count the Stereocenters
In this compound, we have:
- 1 chiral carbon (the one with Cl)
- 1 double bond (which can have two configurations)

Thus, the total number of stereocenters (n) is:
\( n = 1 \text{ (from the chiral carbon)} + 1 \text{ (from the double bond)} = 2 \)

Step 4: Calculate the Number of Stereoisomers
The formula to calculate the number of stereoisomers is given by:
\( \text{Number of stereoisomers} = 2^n \)
Where \( n \) is the number of stereocenters.

Substituting the value of \( n \):
\( \text{Number of stereoisomers} = 2^2 = 4 \)

Conclusion
Therefore, the total number of stereoisomers possible for the compound `CH₃CH=CHCHClCH₃` is 4.

---