If a compound has n asymmetric carbon atoms with different terminal groups, the number of stereoisomers is given by the formula:
(1/2)n
2n
2√n
√2n
The correct Answer is:B
To determine the number of stereoisomers for a compound with n asymmetric carbon atoms that have different terminal groups, we can follow these steps:
1. Identify Asymmetric Carbon Atoms:
- An asymmetric carbon atom (also known as a chiral center) is a carbon atom that is attached to four different groups.
- For our calculation, we need to count how many such asymmetric carbon atoms (n) are present in the compound.
2. Understanding Terminal Groups:
- Terminal groups refer to the groups attached to the ends of the carbon chain. In this case, we are told that these terminal groups are different for each asymmetric carbon atom.
3. Apply the Formula:
- The formula to calculate the number of stereoisomers when there are n asymmetric carbon atoms is given by:
\(
\text{Number of Stereoisomers} = 2^n
\)
- This formula arises because each asymmetric carbon can exist in two configurations (R or S), leading to a total of \(2^n\) combinations for n asymmetric carbons.
4. Example Calculation:
- If we have a compound with 4 asymmetric carbon atoms (n = 4), we can substitute this value into the formula:
\(
\text{Number of Stereoisomers} = 2^4 = 16
\)
- Thus, for 4 asymmetric carbon atoms with different terminal groups, there would be 16 stereoisomers.
5. Conclusion:
- Therefore, the correct answer to the question is that the number of stereoisomers for a compound with n asymmetric carbon atoms with different terminal groups is given by \(2^n\).
Final Answer:
The number of stereoisomers is given by the formula \(2^n\).
- An asymmetric carbon atom (also known as a chiral center) is a carbon atom that is attached to four different groups.
- For our calculation, we need to count how many such asymmetric carbon atoms (n) are present in the compound.
- Terminal groups refer to the groups attached to the ends of the carbon chain. In this case, we are told that these terminal groups are different for each asymmetric carbon atom.
- The formula to calculate the number of stereoisomers when there are n asymmetric carbon atoms is given by:
\(
\text{Number of Stereoisomers} = 2^n
\)
- This formula arises because each asymmetric carbon can exist in two configurations (R or S), leading to a total of \(2^n\) combinations for n asymmetric carbons.
- If we have a compound with 4 asymmetric carbon atoms (n = 4), we can substitute this value into the formula:
\(
\text{Number of Stereoisomers} = 2^4 = 16
\)
- Thus, for 4 asymmetric carbon atoms with different terminal groups, there would be 16 stereoisomers.
- Therefore, the correct answer to the question is that the number of stereoisomers for a compound with n asymmetric carbon atoms with different terminal groups is given by \(2^n\).
The number of stereoisomers is given by the formula \(2^n\).
Topper's Solved these Questions
- ISOMERISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Assertion-Reasoning Type (Exercise)
5 Videos
- ISOMERISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Fill in the blanks (Exercise)
3 Videos
- ISOMERISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Single correct answer type
13 Videos
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Archives Subjective
28 Videos
- NCERT BASED EXERCISEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - Chemical Equilibrium
73 Videos
Similar Questions
An asymmetric carbon atom is a chiral centre.
View SolutionDetermine the number of stereoisomers in the given compound
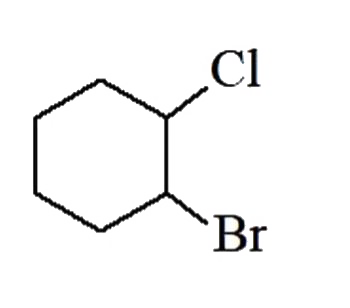
View SolutionTotal number of stereoisomers of given compound are:
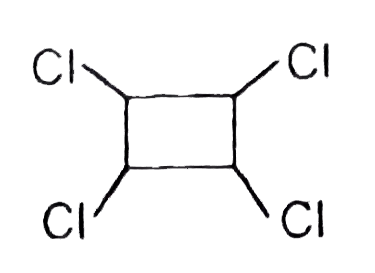
View SolutionNumber of asymmetric carbon atoms in fructose
View SolutionTotal number of stereoisomers of the given molecule?

View SolutionWhat is the maximum number of stereoisomers possible for this compound?
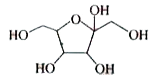
View SolutionWhat is the number of asymmetric carbon atoms in aldopentose?
View SolutionA carbon atom having four different groups is known as
View SolutionTotal number of stereoisomers possible for the following compound is.
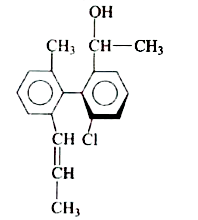
View SolutionWhich of the following has/have asymmetric carbon atom?
View Solution
