Find the electronegativity of lead with the help of the given valus. Screening consitant (σ) of Pb=76.70. Atomic number of lead =82 and covalent radius of Pb=5.3Å
To find the electronegativity of lead (Pb) using the given values, we can follow these steps:
Step 1: Write down the given values
- Screening constant (σ) of Pb = 76.70
- Atomic number (Z) of Pb = 82
- Covalent radius of Pb = 5.3 Å
Step 2: Calculate the effective nuclear charge (Z effective)
The effective nuclear charge (Z effective) can be calculated using the formula:
Zeffective=Z−σ
Substituting the values:
Zeffective=82−76.70=5.30
Step 3: Use the formula for electronegativity
The formula for electronegativity (χ) developed by Allred and Rochow is:
χ=0.359×Zeffectiver2+0.744
where r is the covalent radius.
Step 4: Substitute the values into the formula
Now, substitute Zeffective=5.30 and r=5.3 Å into the formula:
χ=0.359×5.30(5.3)2+0.744
Calculating (5.3)2:
(5.3)2=28.09
Now substituting this value:
χ=0.359×5.3028.09+0.744
Step 5: Calculate the fraction
Calculate 5.3028.09:
5.3028.09≈0.188
Step 6: Multiply and add
Now multiply:
0.359×0.188≈0.0675
Finally, add this to 0.744:
χ≈0.0675+0.744=0.8115
Step 7: Round off the result
Rounding off gives:
χ≈0.812
Thus, the electronegativity of lead (Pb) is approximately 0.812.
---
- Screening constant (σ) of Pb = 76.70
- Atomic number (Z) of Pb = 82
- Covalent radius of Pb = 5.3 Å
The effective nuclear charge (Z effective) can be calculated using the formula:
Zeffective=Z−σ
Zeffective=82−76.70=5.30
The formula for electronegativity (χ) developed by Allred and Rochow is:
χ=0.359×Zeffectiver2+0.744
where r is the covalent radius.
Now, substitute Zeffective=5.30 and r=5.3 Å into the formula:
χ=0.359×5.30(5.3)2+0.744
(5.3)2=28.09
χ=0.359×5.3028.09+0.744
Calculate 5.3028.09:
5.3028.09≈0.188
Now multiply:
0.359×0.188≈0.0675
χ≈0.0675+0.744=0.8115
Rounding off gives:
χ≈0.812
Topper's Solved these Questions
- PERIODIC CLASSIFICATION OF ELEMENTS AND GENERAL INORGANIC CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - PERIODIC CLASSIFICATION OF ELEMENTS AND GENERAL INORGANIC CHEMISTRYEXERCISE - Ex 1.1
14 Videos
- PERIODIC CLASSIFICATION OF ELEMENTS AND GENERAL INORGANIC CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - PERIODIC CLASSIFICATION OF ELEMENTS AND GENERAL INORGANIC CHEMISTRYEXERCISE - Ex 1.1 (Very Short)
22 Videos
- PERIODIC CLASSIFICATION OF ELEMENTS AND GENERAL INORGANIC CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - PERIODIC CLASSIFICATION OF ELEMENTS AND GENERAL INORGANIC CHEMISTRYEXERCISE - Exercises (Archives )Subjective
4 Videos
- P-BLOCK GROUP 14 - CARBON FAMILYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - P-BLOCK GROUP 14 - CARBON FAMILYEXERCISE - Exercises Archives (Subjective)
9 Videos
- PURIFICATION OF ORGANIC COMPOUNDS AND QUALITATIVE AND QUANTITATIVE ANALYSISBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - PURIFICATION OF ORGANIC COMPOUNDS AND QUALITATIVE AND QUANTITATIVE ANALYSISEXERCISE - Assertion Reasoning Type
5 Videos
Similar Questions
A sphere of lead of mass 10 g has net charge −25×10−9C.
(i) Find the number of excess electrons on the sphere.
(ii) How many excess electrons are per lead atom ? Atomic number of lead is 82 and its atomic mass is 207 g/mol.
View SolutionMulliken defined the electronegativity of an atom as the arithmetic mean of its ionisation energy and electron affinity.
XA=12(I.P.+E.A.)
One more relationship given by him, if the values are given in eV is
XA=Ionisation potential+Electron affinity5.6
When there is pure covalent bond between A-B
(IP)A+(EA)A5.6=(IP)B+(EA)B5.6
⇒XA=XB
Pauling's Electronegativity scale is based on
View Solution
Knowledge Check
The radius of hydrogen atom in the ground state 0.53Å. The radius of Li2+ ion (Atomic number = 3) in a similar state is
A1.06 ÅB0.265 ÅC0.17 ÅD0.53 Å
Mulliken defined the electronegativity of an atom as the arithmetic mean of its ionisation energy and electron affinity.
XA=12(I.P.+E.A.)
One more relationship given by him, if the values are given in eV is
XA=Ionisation potential+Electron affinity5.6
When there is pure covalent bond between A-B
(IP)A+(EA)A5.6=(IP)B+(EA)B5.6
⇒XA=XB
According to Mulliken, electronegativity depends on
View SolutionMulliken defined the electronegativity of an atom as the arithmetic mean of its ionisation energy and electron affinity.
XA=12(I.P.+E.A.)
One more relationship given by him, if the values are given in eV is
XA=Ionisation potential+Electron affinity5.6
When there is pure covalent bond between A-B
(IP)A+(EA)A5.6=(IP)B+(EA)B5.6
⇒XA=XB
When there is formation of δ−A−δ+B bond then condition will be
View SolutionJ.C. Slater proposed an empirical constant that represents the cumulative extent to which the other electrons of an atom shield (or screen) any particular electron from the nuclear charge. Thus, slater's screening contant σ is as : Z∗=Z−σ
Here, Z is the atomic number of the atom, and hence is equal to the actual number of protons in the atom. the parameter Z∗ is the effective nuclear charge, which according to is smaller than Z, since the electron in question is screened (shielded) from Z by an amount σ. Conversely, an electron that is well shielded from the nuclear charge Z experiences a small effective nuclear charge Z∗.
The value of σ for any one electron in a given electron configuration (i.e., in the presence of the other electrons of the atom in question) is calculated using a set of empirical rules developed by slater. according to these rules, the value of σ for the electron in question is the cumulative total provided by the various other electrons of the atom.
Q. Which of the following statement is correct?
View SolutionJ.C. Slater proposed an empirical constant that represents the cumulative extent to which the other electrons of an atom shield (or screen) any particular electron from the nuclear charge. Thus, slater's screening contant σ is as : Z∗=Z−σ
Here, Z is the atomic number of the atom, and hence is equal to the actual number of protons in the atom. the parameter Z∗ is the effective nuclear charge, which according to is smaller than Z, since the electron in question is screened (shielded) from Z by an amount σ. Conversely, an electron that is well shielded from the nuclear charge Z experiences a small effective nuclear charge Z∗.
The value of σ for any one electron in a given electron configuration (i.e., in the presence of the other electrons of the atom in question) is calculated using a set of empirical rules developed by slater. according to these rules, the value of σ for the electron in question is the cumulative total provided by the various other electrons of the atom.
Q. The effective nuclear charge at the periphery of chromium atom [Z=24]:
View SolutionJ.C. Slater proposed an empirical constant that represents the cumulative extent to which the other electrons of an atom shield (or screen) any particular electron from the nuclear charge. Thus, slater's screening contant σ is as : Z∗=Z−σ
Here, Z is the atomic number of the atom, and hence is equal to the actual number of protons in the atom. the parameter Z∗ is the effective nuclear charge, which according to is smaller than Z, since the electron in question is screened (shielded) from Z by an amount σ. Conversely, an electron that is well shielded from the nuclear charge Z experiences a small effective nuclear charge Z∗.
The value of σ for any one electron in a given electron configuration (i.e., in the presence of the other electrons of the atom in question) is calculated using a set of empirical rules developed by slater. according to these rules, the value of σ for the electron in question is the cumulative total provided by the various other electrons of the atom.
Q. The effective nuclear charge at the periphery of chromium atom [Z=24]:
View SolutionJ.C. Slater proposed an empirical constant that represents the cumulative extent to which the other electrons of an atom shield (or screen) any particular electron from the nuclear charge. Thus, slater's screening contant σ is as : Z∗=Z−σ
Here, Z is the atomic number of the atom, and hence is equal to the actual number of protons in the atom. the parameter Z∗ is the effective nuclear charge, which according to is smaller than Z, since the electron in question is screened (shielded) from Z by an amount σ. Conversely, an electron that is well shielded from the nuclear charge Z experiences a small effective nuclear charge Z∗.
The value of σ for any one electron in a given electron configuration (i.e., in the presence of the other electrons of the atom in question) is calculated using a set of empirical rules developed by slater. according to these rules, the value of σ for the electron in question is the cumulative total provided by the various other electrons of the atom.
Q. According to Slater's rule, order of effective nuclear charge (Z∗) for last electron in case of Li, Na and K.
View SolutionIn the figure shown, a screen is placed normal to the line joining the two point coherent sources S1andS2. The interference pattern consists of concentric circles.
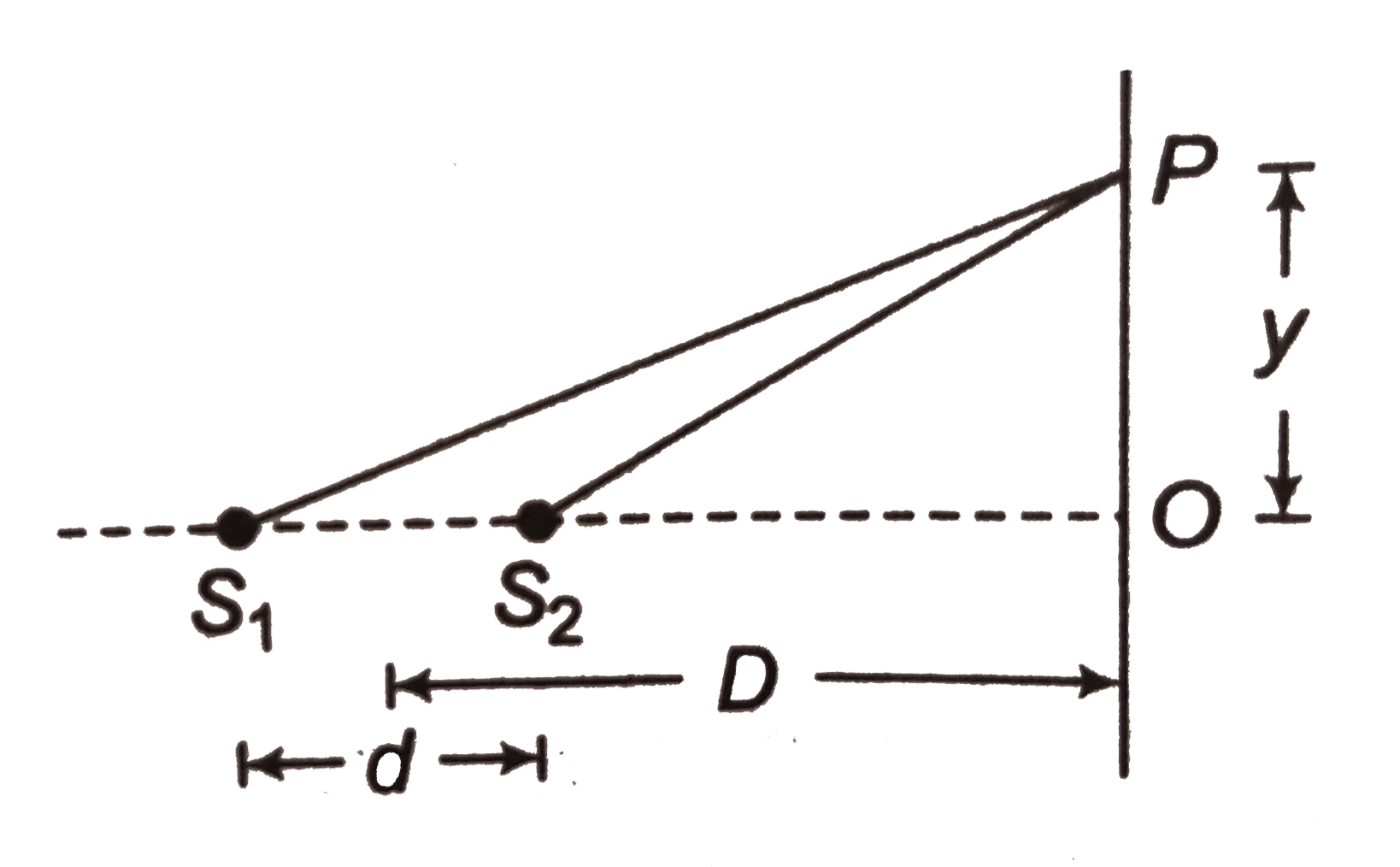
(a)Find the radius of the nth bright ring.
(b) If d=0.5 mm, λ=5000Å and D=100 cm, find the radius of the closest second bright ring.
(c) Also, find the value of n for this ring.
View Solution
