One the basic of CFT predict the geometry of the compund K3[Mn(CN)6] Also calculate the value of μsπn only of the compund .
To solve the problem regarding the compound K3(Mn(CN)6), we will follow these steps:
Step 1: Calculate the Oxidation State of Manganese
Let the oxidation state of manganese be x. The cyanide ion (CN−) has a charge of -1, and since there are 6 cyanide ions, their total contribution is -6. The overall charge of the coordination sphere is -3 due to the presence of 3 potassium ions, each with a +1 charge.
The equation can be set up as follows:
x+6(−1)=−3
x−6=−3
x=+3
Hint: To find the oxidation state, consider the charges contributed by the ligands and the overall charge of the complex.
Step 2: Determine the Electronic Configuration of Mn3+
Manganese has an atomic number of 25, and its electronic configuration is (Ar)4s23d5. When manganese loses 3 electrons to form Mn3+, the configuration becomes:
4s03d4
Hint: Remember that electrons are removed first from the 4s orbital before the 3d orbital.
Step 3: Identify the Coordination Number and Geometry
The coordination number of the complex is 6, as there are 6 cyanide ligands coordinated to the manganese ion. In coordination chemistry, a coordination number of 6 typically leads to an octahedral geometry.
Hint: The coordination number helps determine the geometry; for 6, it is usually octahedral.
Step 4: Analyze the Ligand Field Strength
Cyanide (CN−) is a strong field ligand, which means it has the ability to cause pairing of electrons in the d orbitals. In an octahedral field, the d orbitals split into t2g and eg levels.
Hint: Strong field ligands can cause electron pairing, which affects the number of unpaired electrons.
Step 5: Fill the d Orbitals
With 4 electrons in the 3d orbitals and considering pairing due to the strong field ligand, the filling will be:
- The first three electrons will occupy the t2g orbitals singly.
- The fourth electron will pair with one of the existing electrons in the t2g orbitals.
Thus, the configuration in the d orbitals will be:
(t2g)4(eg)0
This results in 2 unpaired electrons.
Hint: Visualize the d orbital splitting and how electrons fill according to Hund's rule and pairing.
Step 6: Calculate the Spin-Only Magnetic Moment
The formula for calculating the spin-only magnetic moment μspin is given by:
μspin=√n(n+2)
where n is the number of unpaired electrons. Here, n=2.
Substituting the value:
μspin=√2(2+2)=√2×4=√8=2.83Bohr magnetons
Hint: Use the formula for spin-only magnetic moment to find the magnetic properties of the complex.
Final Results
- Geometry of the compound: Octahedral
- Spin-only magnetic moment: 2.83Bohr magnetons
Let the oxidation state of manganese be x. The cyanide ion (CN−) has a charge of -1, and since there are 6 cyanide ions, their total contribution is -6. The overall charge of the coordination sphere is -3 due to the presence of 3 potassium ions, each with a +1 charge.
x+6(−1)=−3
x−6=−3
x=+3
Manganese has an atomic number of 25, and its electronic configuration is (Ar)4s23d5. When manganese loses 3 electrons to form Mn3+, the configuration becomes:
4s03d4
The coordination number of the complex is 6, as there are 6 cyanide ligands coordinated to the manganese ion. In coordination chemistry, a coordination number of 6 typically leads to an octahedral geometry.
Cyanide (CN−) is a strong field ligand, which means it has the ability to cause pairing of electrons in the d orbitals. In an octahedral field, the d orbitals split into t2g and eg levels.
With 4 electrons in the 3d orbitals and considering pairing due to the strong field ligand, the filling will be:
- The first three electrons will occupy the t2g orbitals singly.
- The fourth electron will pair with one of the existing electrons in the t2g orbitals.
(t2g)4(eg)0
This results in 2 unpaired electrons.
The formula for calculating the spin-only magnetic moment μspin is given by:
μspin=√n(n+2)
where n is the number of unpaired electrons. Here, n=2.
μspin=√2(2+2)=√2×4=√8=2.83Bohr magnetons
- Geometry of the compound: Octahedral
- Spin-only magnetic moment: 2.83Bohr magnetons
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Ex 7.1 Subjective (Terminology)
5 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Ex 7.1 Subjective (Effective Atomic Number (Ean))
3 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Archives Subjective
23 Videos
- D AND F BLOCK ELEMENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Archives Subjective
29 Videos
Similar Questions
The spin magnetic moment of iron in K3[Fe(CN)6]
View Solution27.6gK2CO3 was treated by a series of reagents so as to convent all of its carbon to K2Zn3[Fe(CN)6]2 Calculate the weight of the product [mol.wt. of K2CO3=138 and mol. Wt. of K2Zn3[Fe(CN)6]2=698] .
View Solution27.6gK2CO3 was treated by a series of reagents so as to convent all of its carbon to K2Zn3[Fe(CN)6]2 Calculate the weight of the product [mol.wt. of K2CO3=138 and mol. Wt. of K2Zn3[Fe(CN)6]2=698] .
View SolutionMagnetic moment value of [Mn(CN)6]3− ion in 2.8BM Predict the type of hybridisation and geometry of the ion .
View SolutionThe line given by the equation 2x−y3=7 passes through the point (k,6), calculate the value of k.
View SolutionWhat is the expected value of van't Hoff factor for K3[Fe(CN)6] in dilute solution?
View SolutionThe coefficient of static and kinetic friction between the two blocks and also between the lower block and the ground are μs=0.6andμk=0.4 Find the value of tension T applied on the lower block at which the upper block begins to slip relative to lower block.
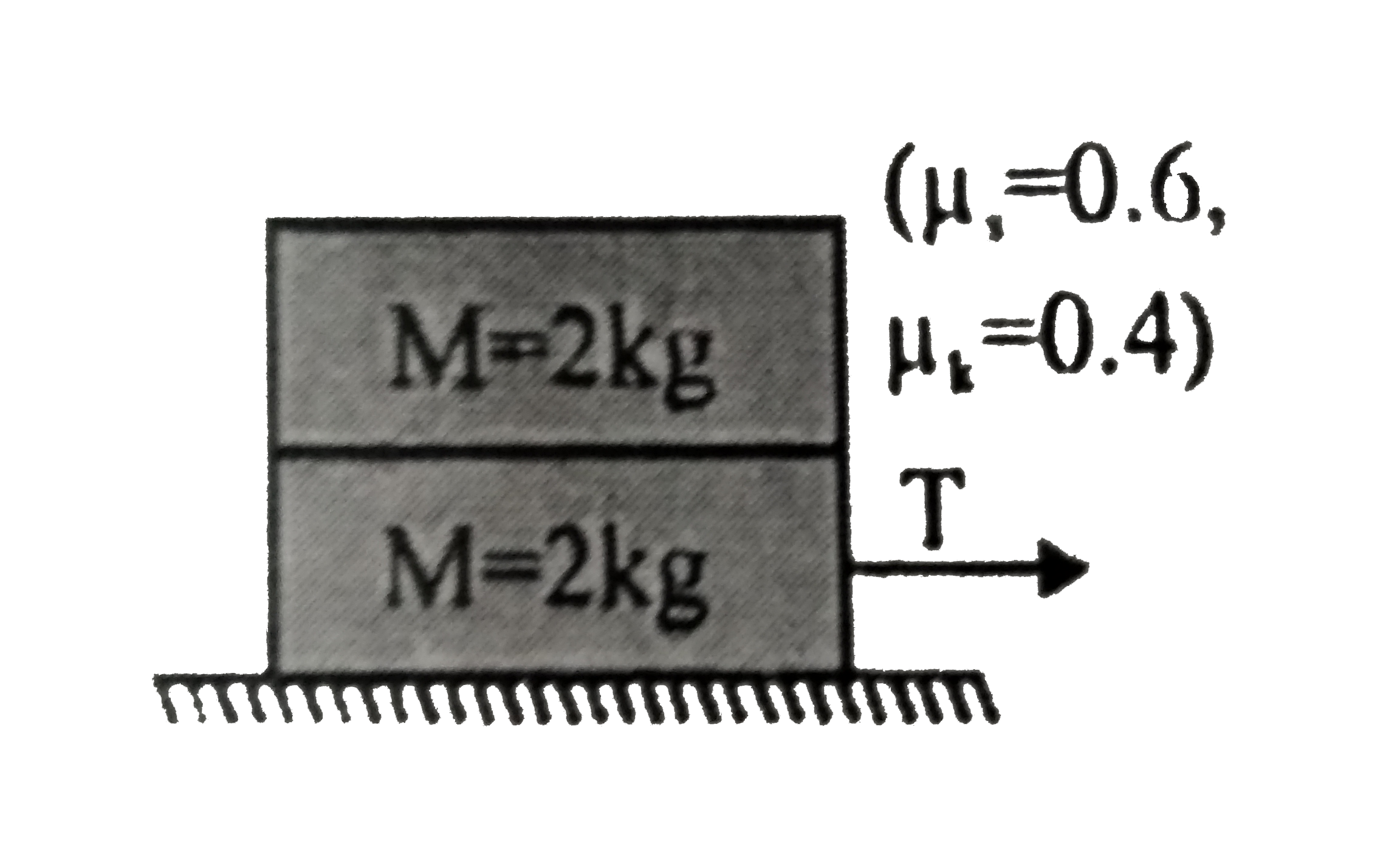
View SolutionAssertion:- K3[Fe(CN)6] is an example of low spin complex.
Reason:- This complex is paramagnetic in nature.
View SolutionThe ratio of the value of any collogative property for K4[Fe(CN)6] solution to that of Fe4[Fe(CN)6]3(prussian blue,)solution is nearly
View SolutionOne the basis of VBT answer the following complex ions
[Ti(bpy)3]Θ
(a) Type of hybridisation involed
(b) Type of inner or outer orbital octahedral complex
(c ) Magnetic behaviour and μsπn value .
View Solution
