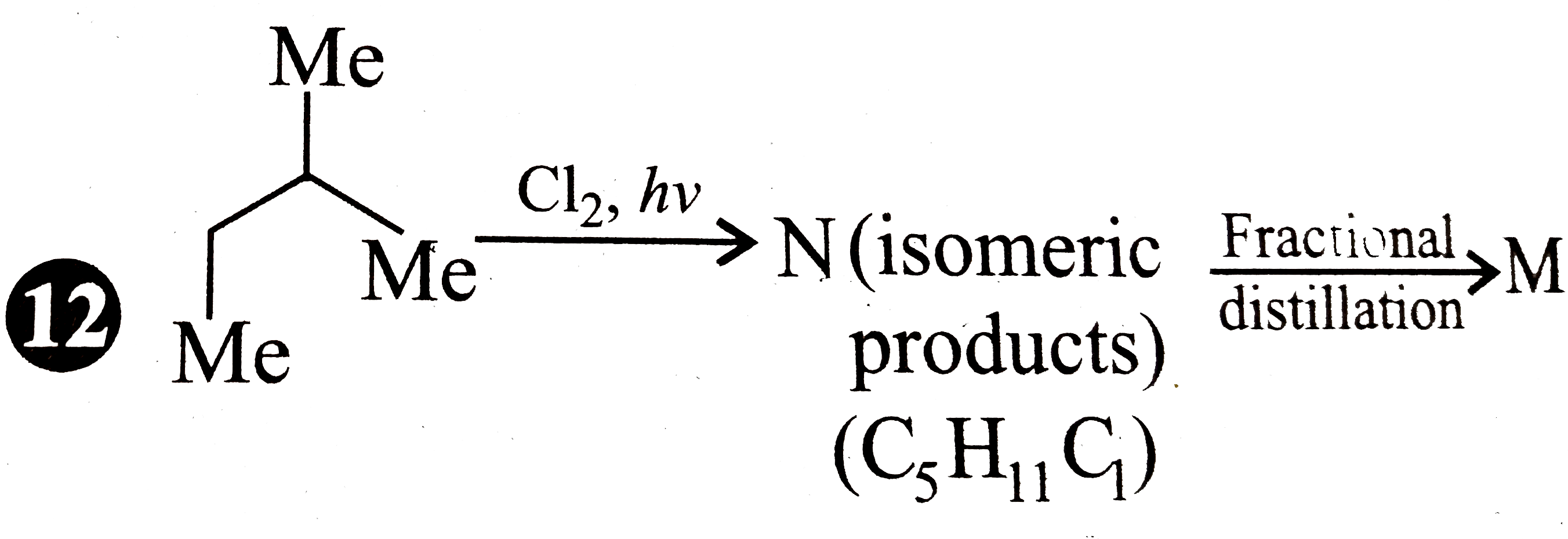What are the values of m and n in the anionic species [V(CO)m]n− if it is fllowing Sidwick EAN rule and having octahedral shape ? .
The correct Answer is:6,1
To solve the problem of determining the values of m and n in the anionic species (V(CO)m)n− while following the Sidwick EAN rule and having an octahedral shape, we can follow these steps:
Step 1: Understand the Coordination Number
The question states that the complex has an octahedral shape. In coordination chemistry, an octahedral complex has a coordination number of 6. Therefore, the value of m (the number of CO ligands) is 6.
Hint: Remember that the coordination number corresponds to the number of ligand donor sites surrounding the central metal atom in an octahedral geometry.
Step 2: Write the EAN Formula
According to the Sidwick EAN rule, the effective atomic number (EAN) of the central metal atom is given by the formula:
EAN=Z−x+2L
Where:
- Z is the atomic number of the central metal atom (Vanadium, V, has an atomic number of 23).
- x is the oxidation state of the central metal atom.
- L is the number of lone pair donating sites from the ligands.
Step 3: Calculate the Number of Lone Pairs
Since carbon monoxide (CO) is a neutral ligand and each CO donates one lone pair, and we have 6 CO ligands, the total number of lone pair donating sites L is 6.
Step 4: Set Up the EAN Equation
Now, substituting the known values into the EAN formula:
36=23−x+2×6
This simplifies to:
36=23−x+12
Step 5: Solve for the Oxidation State x
Rearranging the equation gives:
36=35−x
So,
x=−1
This means the oxidation state of Vanadium in this complex is −1.
Step 6: Determine the Charge of the Complex
The overall charge of the complex can be calculated as follows:
The oxidation state of Vanadium is −1, and since CO is a neutral ligand, the charge contributed by the ligands is 0. Therefore, the overall charge of the complex is:
−1+0=−n
Thus, we have:
−n=−1⟹n=1
Conclusion
The values of m and n in the anionic species (V(CO)m)n− are:
- m=6
- n=1
Final Answer:
The values of m and n are m=6 and n=1.
---
The question states that the complex has an octahedral shape. In coordination chemistry, an octahedral complex has a coordination number of 6. Therefore, the value of m (the number of CO ligands) is 6.
According to the Sidwick EAN rule, the effective atomic number (EAN) of the central metal atom is given by the formula:
- Z is the atomic number of the central metal atom (Vanadium, V, has an atomic number of 23).
- x is the oxidation state of the central metal atom.
- L is the number of lone pair donating sites from the ligands.
Since carbon monoxide (CO) is a neutral ligand and each CO donates one lone pair, and we have 6 CO ligands, the total number of lone pair donating sites L is 6.
Now, substituting the known values into the EAN formula:
Rearranging the equation gives:
The overall charge of the complex can be calculated as follows:
The values of m and n in the anionic species (V(CO)m)n− are:
- n=1
The values of m and n are m=6 and n=1.
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Exercises Integer (Isomerism)
15 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Exercises Integer (Hybridisation , Vbt , Cft And Application)
13 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Exercises Assertion Reasoning
25 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Archives Subjective
23 Videos
- D AND F BLOCK ELEMENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Archives Subjective
29 Videos
Similar Questions
Knowledge Check
When the value of n = 2, m can have
A1 valueB3 valuesC4 valuesD7 values.
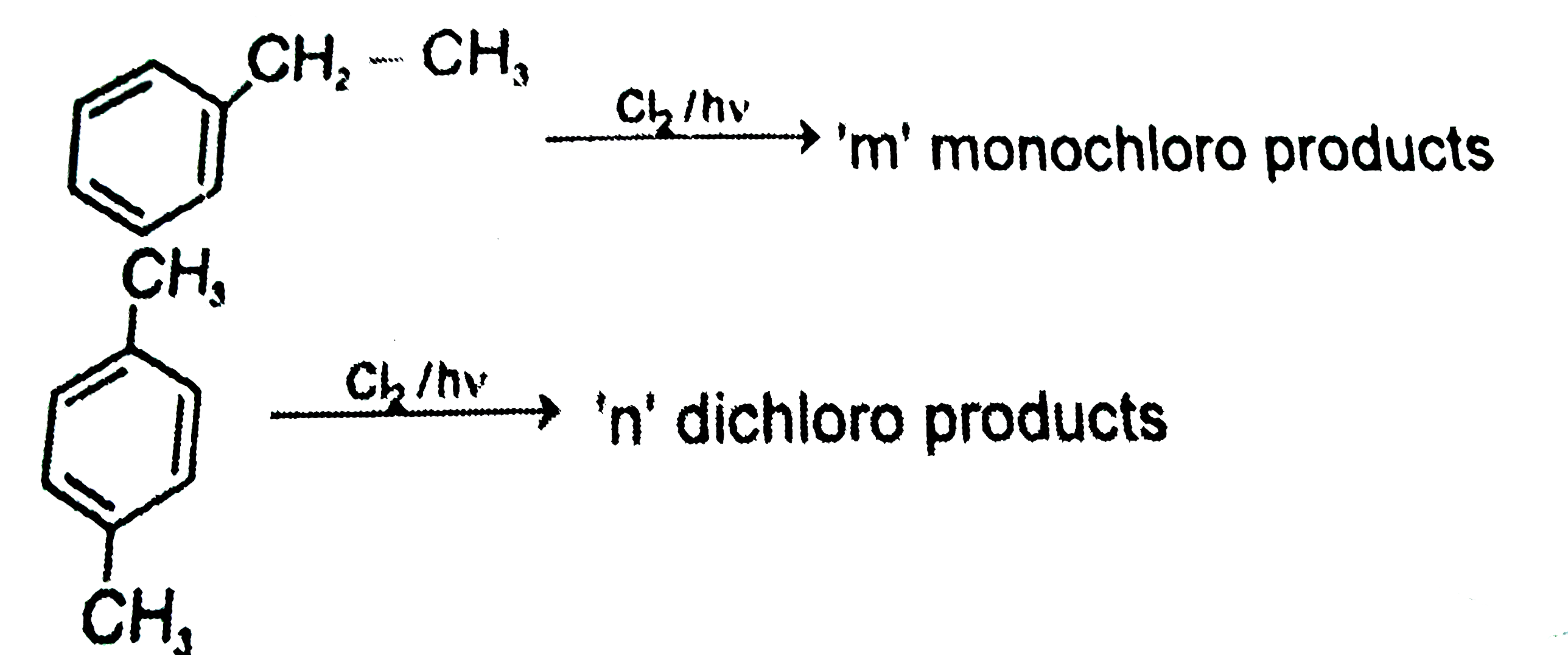
The value of m and n are respectively :
View Solution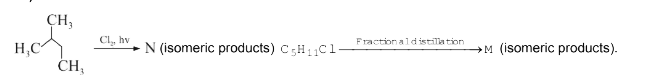
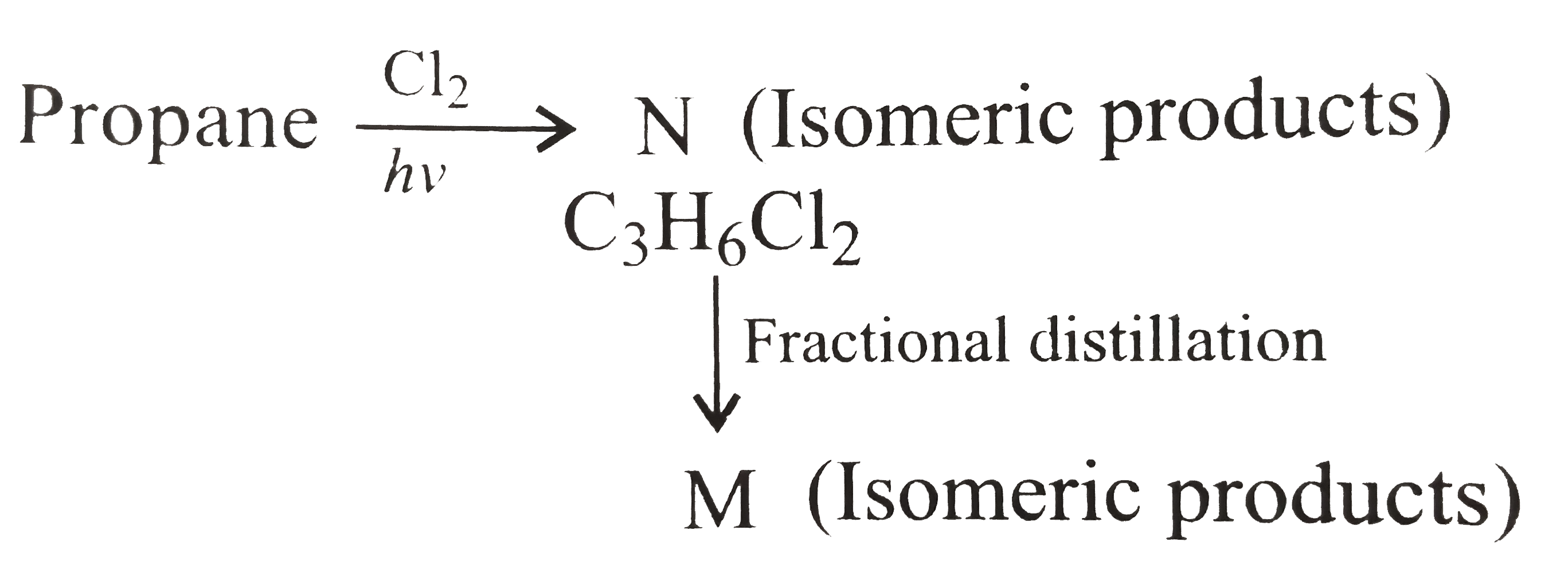
What are N and M ?
View Solution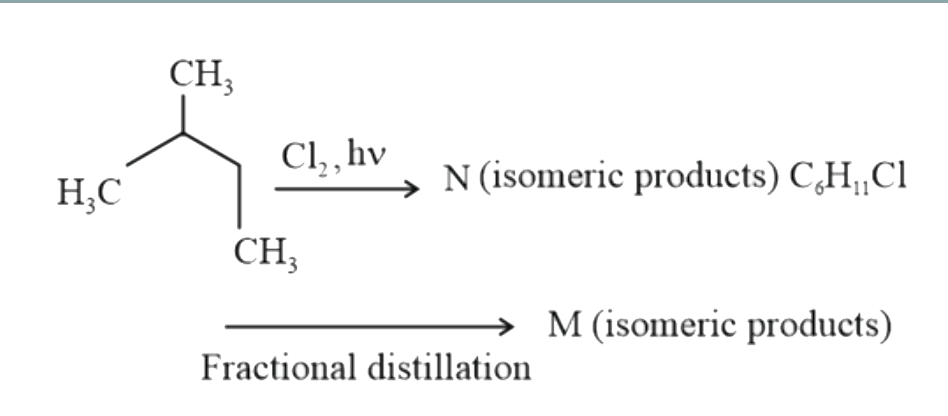
What are N and M ?
View Solution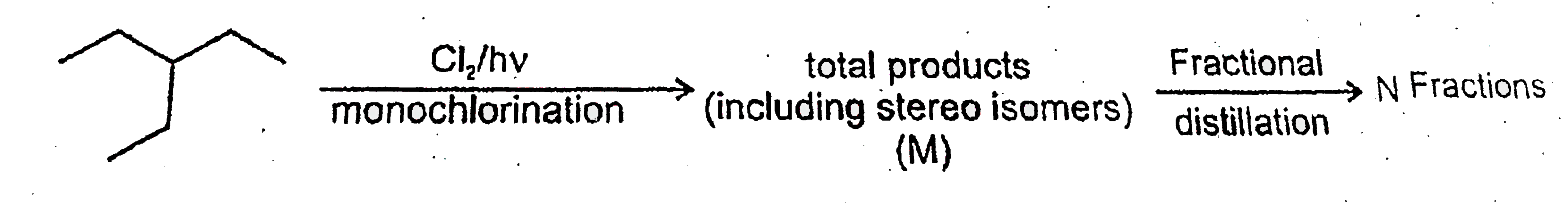
The value of M and N are respectively.
View Solution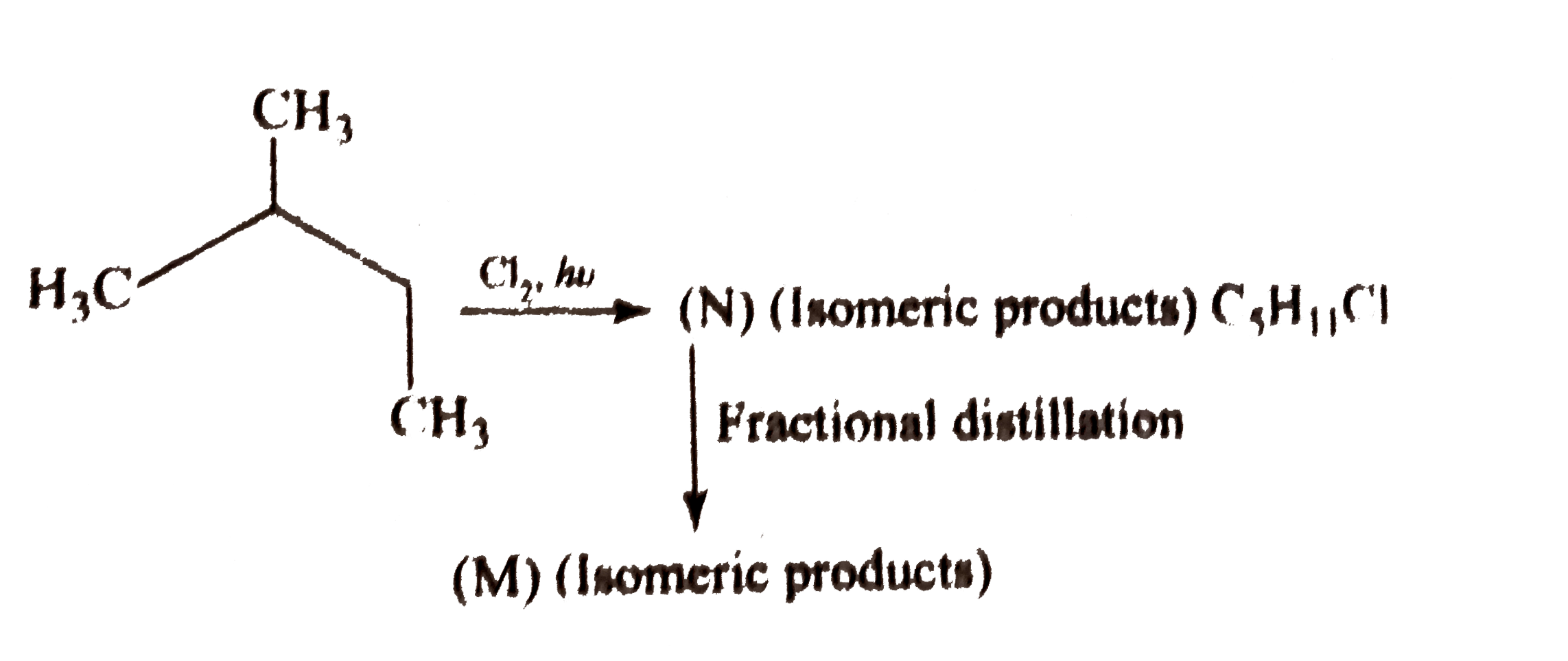
The numberical values of (N) and (M) are :
View SolutionThe value of (m+n)2+(m−n)2 is:
View SolutionFind the values of m and n, in each case, If:
(4,−3) on reflection in x-axis gives (−m,n).
View Solution