Give the ration of geometrical isomers in [M(AA)2b2] and optical isomers of [M(AA)3] .
The correct Answer is:1
To solve the problem of finding the ratio of geometrical isomers in the complex (M(AA)2B2) and optical isomers in the complex (M(AA)3), we will follow these steps:
Step 1: Analyze the complex (M(AA)2B2)
1. Identify the ligand arrangement: The complex has two bidentate ligands A (denoted as AA) and two monodentate ligands B.
2. Determine possible geometrical isomers:
- Cis form: Both AA ligands are adjacent to each other.
- Trans form: The AA ligands are opposite each other.
Thus, there are two geometrical isomers: one cis and one trans.
Step 2: Analyze the complex (M(AA)3)
1. Identify the ligand arrangement: The complex has three bidentate ligands A (denoted as AA).
2. Determine possible optical isomers:
- The arrangement of three bidentate ligands leads to a chiral structure, meaning it can exist in two enantiomeric forms (D and L).
- Since there are no planes of symmetry in this arrangement, it will have two optical isomers.
Step 3: Calculate the ratio of geometrical to optical isomers
- Geometrical isomers in (M(AA)2B2) = 2
- Optical isomers in (M(AA)3) = 2
The ratio of geometrical isomers to optical isomers is:
Ratio=Geometrical IsomersOptical Isomers=22=1
Final Answer
The ratio of geometrical isomers in (M(AA)2B2) to optical isomers in (M(AA)3) is 1.
---
2. Determine possible geometrical isomers:
- Cis form: Both AA ligands are adjacent to each other.
- Trans form: The AA ligands are opposite each other.
2. Determine possible optical isomers:
- The arrangement of three bidentate ligands leads to a chiral structure, meaning it can exist in two enantiomeric forms (D and L).
- Since there are no planes of symmetry in this arrangement, it will have two optical isomers.
- Optical isomers in (M(AA)3) = 2
Ratio=Geometrical IsomersOptical Isomers=22=1
The ratio of geometrical isomers in (M(AA)2B2) to optical isomers in (M(AA)3) is 1.
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Exercises Integer (Hybridisation , Vbt , Cft And Application)
13 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Exercises Fill The Blanks
32 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Exercises Integer (Naming And Terminology)
16 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Archives Subjective
23 Videos
- D AND F BLOCK ELEMENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Archives Subjective
29 Videos
Similar Questions
Give the number of geometrical isomers in [Pt(gly)2] .
View SolutionWhich is the pair of geometrical isomers :

View SolutionWhich can show geometrical isomer ?
View SolutionWrite the sum of geometrical isomers in [Ma2b2c2] complex and stereoisomers in [M(AB)3] complex .
View SolutionGeometrical isomers differ in
View SolutionWhich is a pair of geometrical isomers?
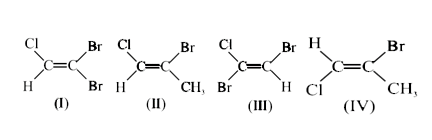
View SolutionWhich is a pair of geometrical isomers?
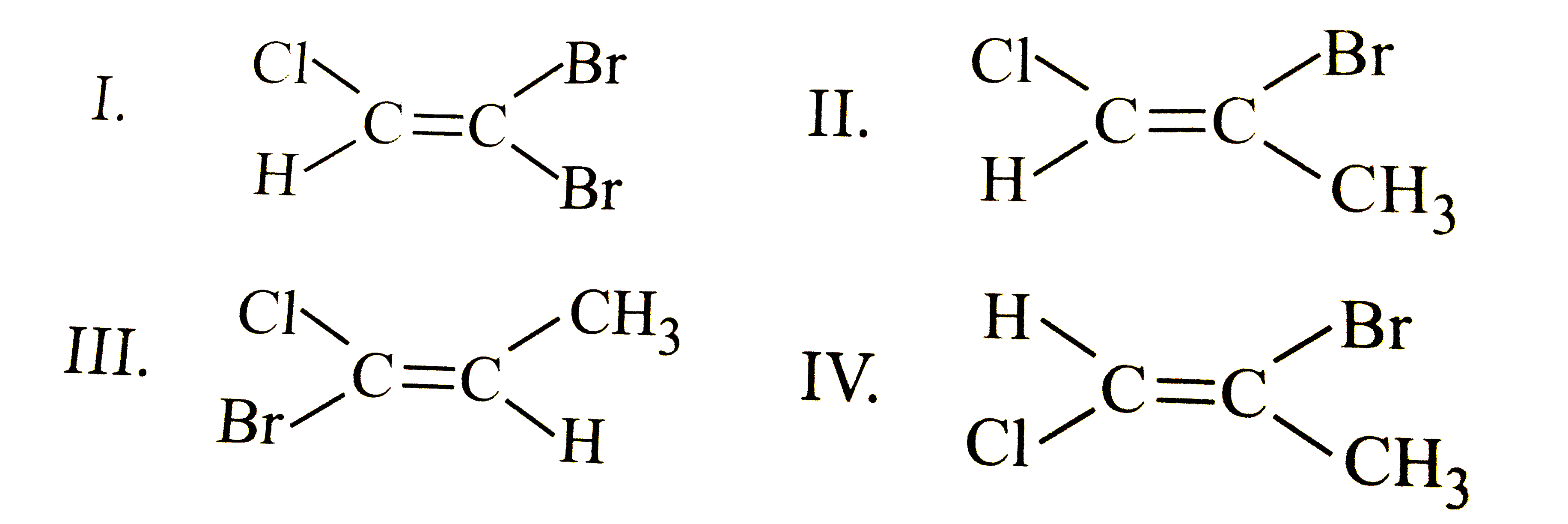
View SolutionGeometrical isomers differ in:
View SolutionFind the number of geometrical isomers in [Co(en)(Pn)(NO2)2]
 .
.
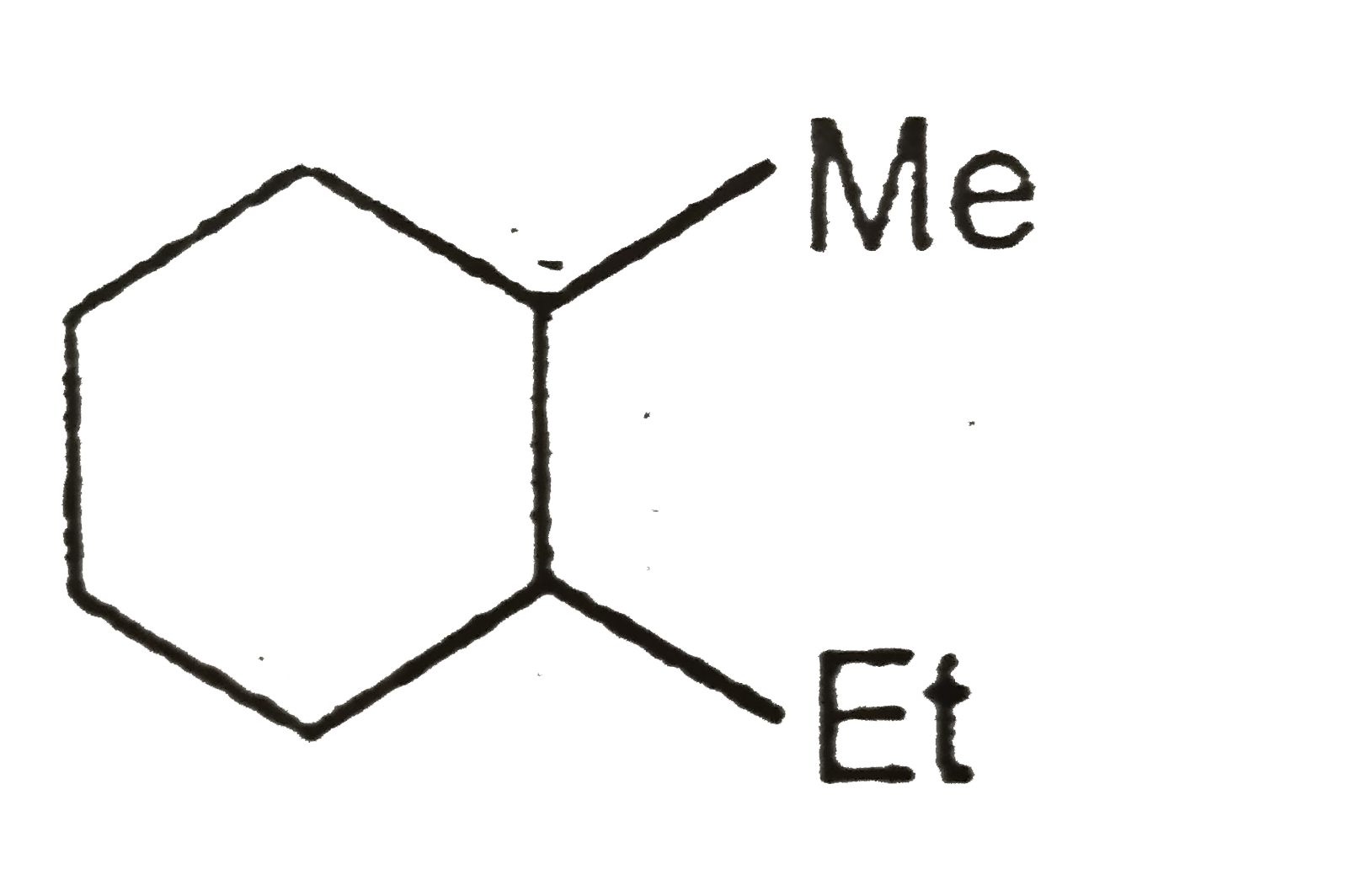
View SolutionNumber of geometrical isomers possible of
View Solution
