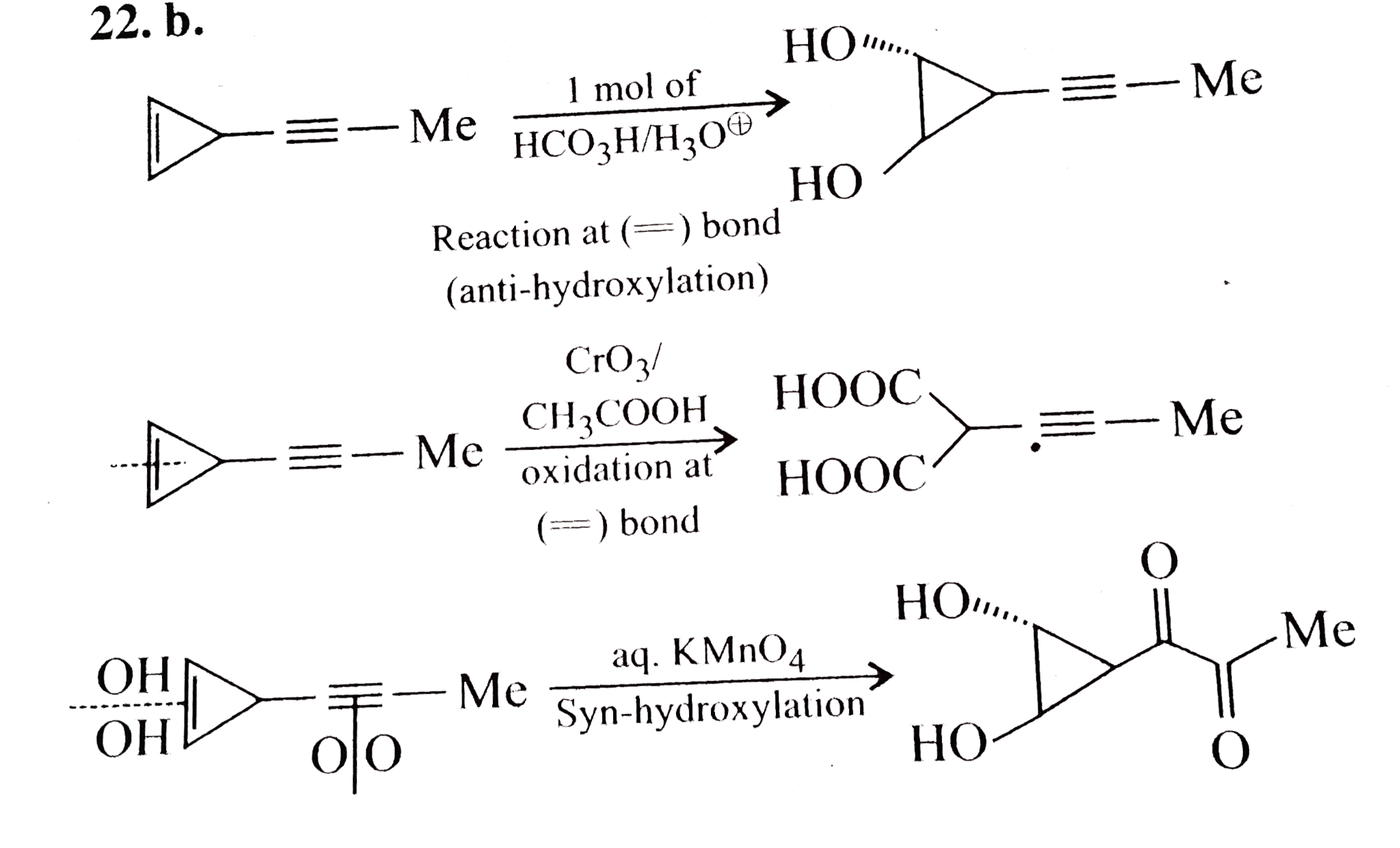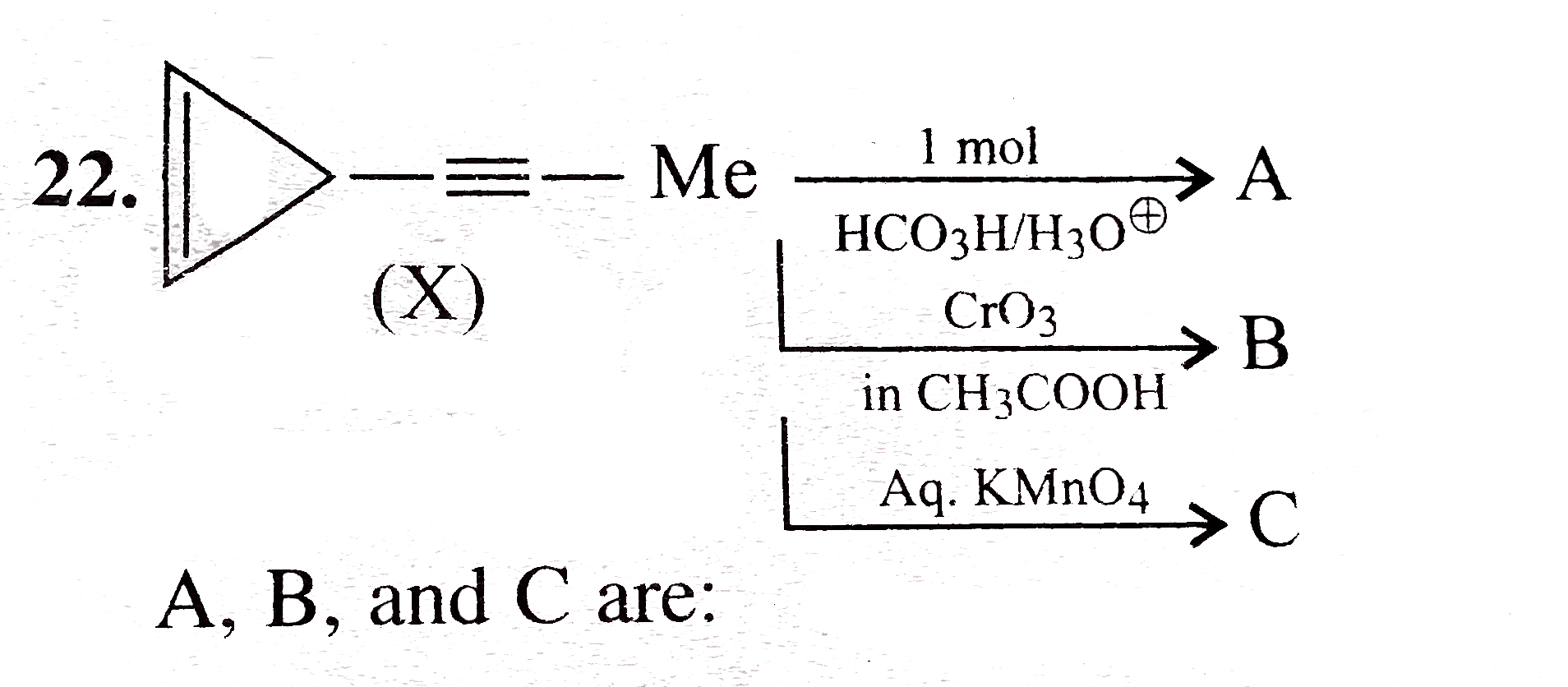
A, B, and C:
The correct Answer is:B
Topper's Solved these Questions
- ALKYNESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKYNESEXERCISE - Exercises (Archives - Single Correct Answer Type)
6 Videos
- ALKYNESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKYNESEXERCISE - Exercises (Archives - Fill in the Blanks Type)
3 Videos
- ALKYNESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKYNESEXERCISE - Exercises (Multiple Correct Answers Type)
25 Videos
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKENES AND ALKADIENESEXERCISE - Single correct Answer
14 Videos
- APPENDIX - INORGANIC VOLUME 1BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - APPENDIX - INORGANIC VOLUME 1EXERCISE - chapter-7 Single correct answer
1 Videos
Similar Questions
In Fig, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then, (a)AD=AB+BC+CA (b)2AD=AB+BC+CA (c)3AD=AB+BC+CA (d)4AD=AB+BC+CA
View SolutionIf in a triangle ABC angle B=900 then tan2(A2) is b−ca (b) b−cb+c (c) b+cb−c (d) b+ca
View SolutionIf ABC ≅ACB, then ABC is isosceles with
(a)AB=AC (b) AB=BC (c) AC=BC (d) None of these
View SolutionIf a,b,c∈Randa(a+b)+b(b+c)+c(c+a)=0 then a.a=b=c=0 b. a+b+c+=0 c. (a−b)2+(b−c)2+(c−a)2=0 d. a3+b3+c3+3abc=0
View SolutionIn ABC , ray AD bisects ∠A and intersects BC in D . If BC=a , AC=b and AB=c , prove that BD=acb+c (ii) D C = abb+c
View SolutionUsing the factor theorem it is found that a+b , b+c and c+a are three factors of the determinant ∣∣ ∣∣−2aa+ba+cb+a−2bb+cc+ac+b−2c∣∣ ∣∣. The other factor in the value of the determinant is
View SolutionIf a,b,c are in G.P. then prove that a2+ab+b2bc+ca+ab=b+ac+b
View SolutionIf the centroid of the triangle formed by the points (a, b), (b, c) and (c, a) is at the origin, then a3+b3+c3= abc (b) 0 (c) a+b+c (d) 3 abc
View SolutionUsing the factor theorem it is found that a+b,b+c and c+a are three factors of the determinant ∣∣ ∣∣−2aa+ba+cb+a−2bb+cc+ac+b−2c∣∣ ∣∣. The other factor in the value of the determinant is (a)4 (b) 2 (c)a+b+c (d) none of these
View SolutionIn ABC , a line XY parallel to BC cuts AB at X and AC at Y . If BY bisects ∠XYC , then (a)BC=CY (b) BC=BY (c) BC≠CY (d) BC≠BY
View Solution