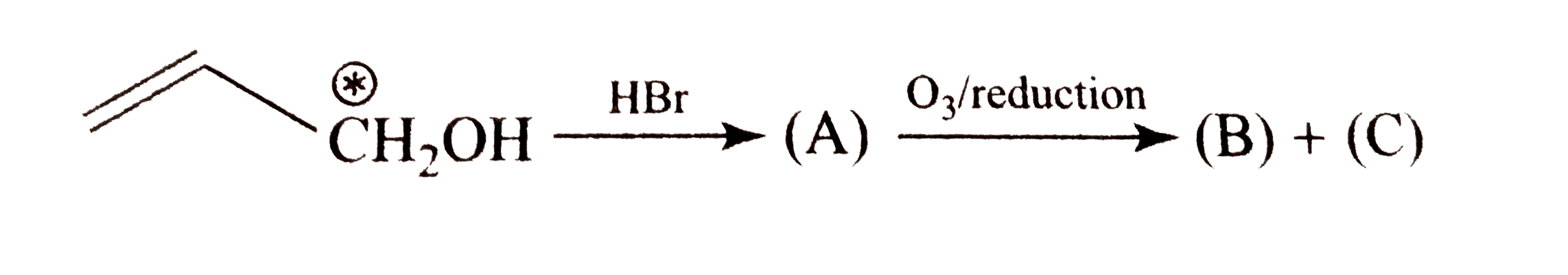
(A),(B), and (C) are :
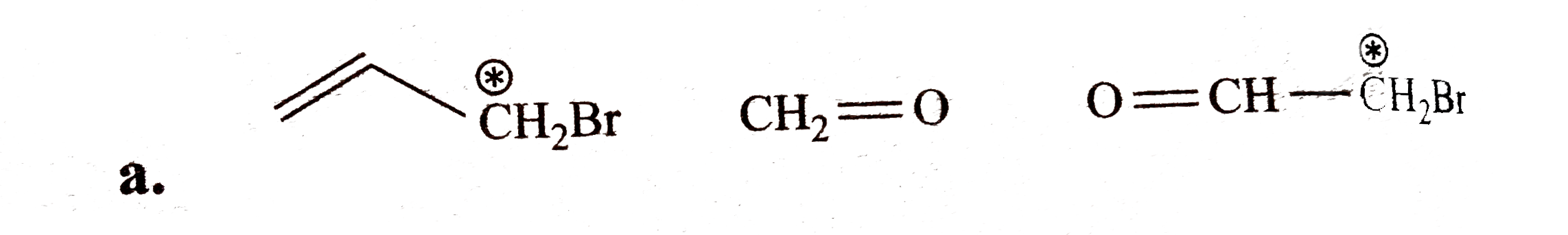
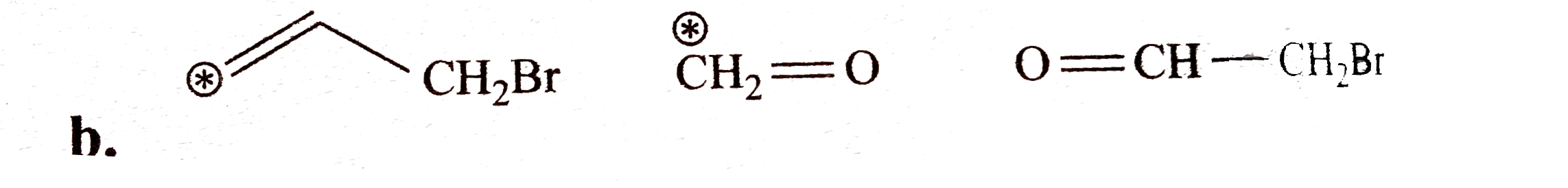
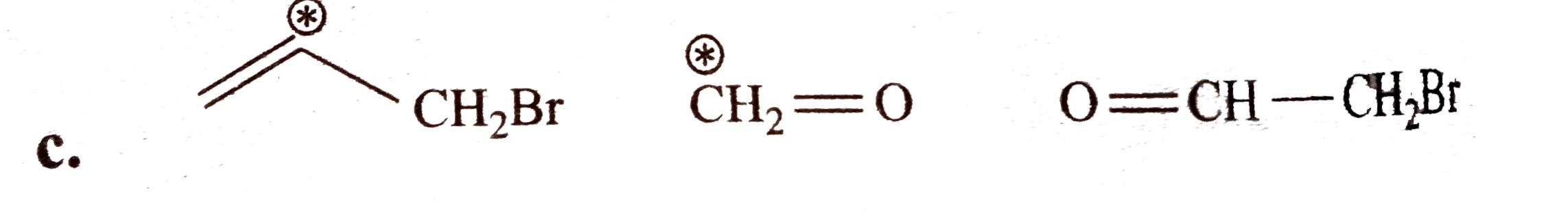
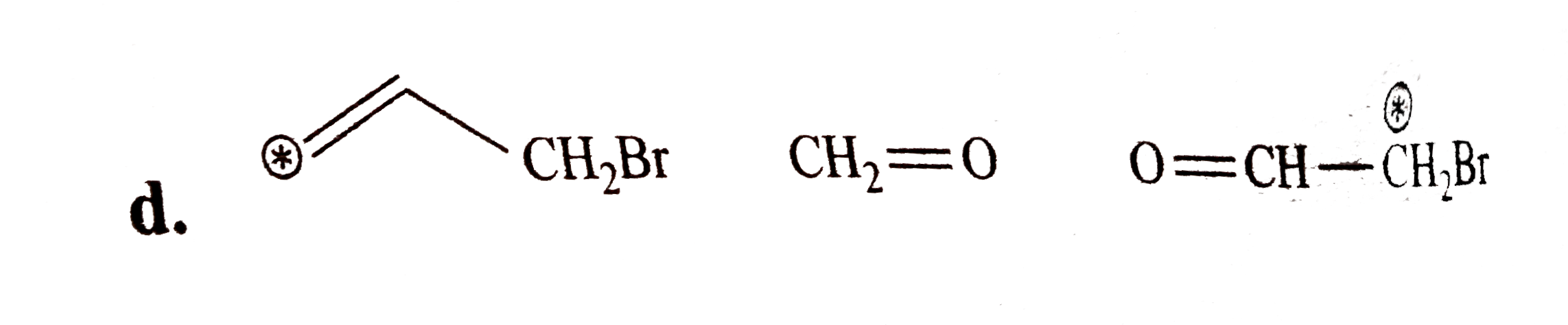
The correct Answer is:b.
Topper's Solved these Questions
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKENES AND ALKADIENESEXERCISE - Archives(ASSERTION-REASIOING)
4 Videos
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKENES AND ALKADIENESEXERCISE - Fill in the Blanks
3 Videos
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKENES AND ALKADIENESEXERCISE - Multiple Correct Answer Type
41 Videos
- ALKANES AND CYCLOALKANESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKANES AND CYCLOALKANESEXERCISE - Archives
13 Videos
- ALKYNESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ALKYNESEXERCISE - Exercises (Archives - Analytical and Desriptive Type)
4 Videos
Similar Questions
In Fig, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then, (a)AD=AB+BC+CA (b)2AD=AB+BC+CA (c)3AD=AB+BC+CA (d)4AD=AB+BC+CA
View SolutionIf a,b,c are in G.P. then the value of ∣∣ ∣∣aba+bbcb+ca+bb+c0∣∣ ∣∣= (A) 1 (B) -1 (C) a+b+c (D) 0
View SolutionIf the centroid of the triangle formed by the points (a, b), (b, c) and (c, a) is at the origin, then a3+b3+c3= abc (b) 0 (c) a+b+c (d) 3 abc
View SolutionIf (a−b), (b−c),(c−a) are in G.P. then prove that (a+b+c)2=3(ab+bc+ca)
View SolutionIf ∣∣ ∣∣a−b−c2a2a2bb−a−c2b2c2cc−a−b∣∣ ∣∣=(a+b+c)(x+a+b+c)2 then the value of x is equal to (A) −2(a+b+c) (B) a+b+c (C) −(a+b+c) (D) 2(a+b+c)
View SolutionUsing the factor theorem it is found that a+b,b+c and c+a are three factors of the determinant ∣∣ ∣∣−2aa+ba+cb+a−2bb+cc+ac+b−2c∣∣ ∣∣. The other factor in the value of the determinant is (a)4 (b) 2 (c)a+b+c (d) none of these
View SolutionUsing the factor theorem it is found that a+b , b+c and c+a are three factors of the determinant ∣∣ ∣∣−2aa+ba+cb+a−2bb+cc+ac+b−2c∣∣ ∣∣. The other factor in the value of the determinant is
View SolutionIf a, b, c are in HP., then ab+c,bc+a,ca+b are in
View SolutionIn ABC , a line XY parallel to BC cuts AB at X and AC at Y . If BY bisects ∠XYC , then (a)BC=CY (b) BC=BY (c) BC≠CY (d) BC≠BY
View SolutionThe expression (a−b)3+ (b−c)3+ (c−a)3 can be factorized as
(a)(a−b)(b−c)(c−a)
(b) 3(a−b)(b−c)(c−a)
(c)−3 (a−b)(b−c)(c−a)
(d)(a+b+c)(a2+b2+c2−ab−bc−ca)
View Solution

