समांतर क्रम में जुड़े C1और C2(C2>C1) धारिताओं के दो संधारित्रों की प्रभावी धारिता, श्रेणीक्रम में उनके संयोजन की प्रभावी धारिता की 256 गुना है। अनुपात C1C2 है
23
43
53
256
The correct Answer is:A
Cसमांतर=256Cश्रेणी
⇒C1+C2=256C1C2C1+C2
⇒6(C1+C2)2=25C1C2
⇒6C21+6C22=12C1C2=25C1C2
⇒6C21C22+6+12C1C2=25C1C2
⇒6C21C22−13C1C2+6=0
यह द्विघात समीकरण है हल करने पर हमें प्राप्त होता है
C2C1=32
Topper's Solved these Questions
Similar Questions
5000A तरंगदैर्ध्य का प्रकाश 1μm चौड़ाई की एक स्लिट पर आपतित होता है। केंद्रीय उच्चिष्ठ की कोणीय चौड़ाई होगी:
05:33View Solutionव्यक्ति A, 25 cm और 200 cm के बीच की वस्तुओं को स्पष्ट रूप से देख सकता है। किसी व्यक्ति B के लिए स्पष्ट दृष्टि की परास का चयन कीजिए, जिसकी मांसपेशियाँ A से अधिक मजबूत हैं, लेकिन नेत्र के अन्य सभी प्राचाल A के समरूप हैं।
05:59View SolutionIIf y=1+c_1/(x-c_1)+(c_2x)/((x-c_1)(x-c_2))+(c_3 x^2)/((x-c_1)(x-c_2)(x-c_3)) show that dy/dx=(y/x)[c_1/(c_1-x)+c_2/(c_2-x)+c_3/(c_3-x)]
02:06View Solution∣∣ ∣ ∣∣111nc1n+1c1n+2c1n+1c2n+2c2n+3c2∣∣ ∣ ∣∣=1
05:55View SolutionDefine centre of curvature.
06:24View SolutionC0C1+C1C2+C2C3+…+Cn−1Cn=
07:38View SolutionIf (C0+C1)(C1+C2)…(Cn−1+Cn)=kC0C1C2…Cn then k=
03:33View Solution(C0+C1)(C1+C2)(C2+C3)………(Cn−1+Cn)C0C1C2…Cn
04:49View SolutionLet C1and C2 be two circles with C2 lying inside C1 A circle C lying inside C1 touches C1 internally and C2 externally. Identify the locus of the centre of C
03:21View SolutionThe value of ∣∣111nCn+21Cn+41Cn1Cn+22Cn+42C2∣∣ is
02:04View Solutionदिखाए गये चित्रानुसार दोनो वृतों के केंद्रों C1 तथा C2 के मध्य दुरी 35 है अर्थात C1C2=35 तथा C1 व C2 केंद्रों वाले वृतों की त्रिज्याएँ क्रमशः 12 व 9 है । यदि वृतों की उभयनिष्ठ आंतरिक स्पर्श रेखा तथा C1C2 का प्रतिच्छेद बिंदु P है, तो l(C1P) का मान होगा
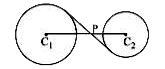
(i) 18 (ii) 20 (iii) 12 (iv) 1506:59View SolutionGiven that CrCr−1=n−r+1r Evaluate C1C0,C2C1 and C3C2
03:54View SolutionIf f(x) is a differentiable function wherever it is continuous and f'(c1)=f'(c2)=0 f''(c1).f''(c2)<0,f(c1)=5,f(c2)=0 and (c1<c2) . If f(x) is continuous in [c1,c2] and f''(c1)−f''(c2)>0 then minimum number of roots of f'(x)=0 in [c1−1,c2+1] is
08:02View SolutionIn the ambiguous case, if a,bandA are given and c1,c2 are the two values of the third (c1−c2)2+(c1+c2)2tan2A is equal to
03:44View SolutionEvaluate |^x C_1^x C_2^x C_3^y C_1^y C_2^y C_3^z C_1^z C_2^z C_3|
02:08View Solution

