Three vector →A,→B and →C add up to zero. Find which is false ?
→A×(→B×→C) is not zero unless →B.→C are parallel
→A(→B×→C) is not zero unless →B.→C are parallel
If →A,→B→C define a plane, →A×(→B×→C) is in that plane
→A.(→B×→C) =0
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
Knowledge Check
Three vectors →A,→B and →C add up to zero.Find which is false.
A(→A×→B)×→C is not zero unless →B,→C are parallelB(→A×→B).→C is not zero unless →B,→C are parallelCIf →A,→B,→C define a plane, (→A×→B)×→C is in that planeD(→A×→B).→C=∣∣→A∣∣∣∣→B∣∣∣∣→C∣∣→C2=A2+B2Three vectors A, B and C add upto zero. Find which is false.
A(→A×→B)×→C is not zero unless →B,→C are parallel.B(→A×→B)⋅→C is not zero unless →B,→C are parallel.CIf →A,→B,→C define a plane, (→A×→B)×→C is in that plane.D(→A×→B)⋅→C=∣∣→A∣∣∣∣→B∣∣∣∣→C∣∣→C2=A2+B2.In a righht angled triangle the three vectors →a,→b and →c add to zero. Then →a,→b is
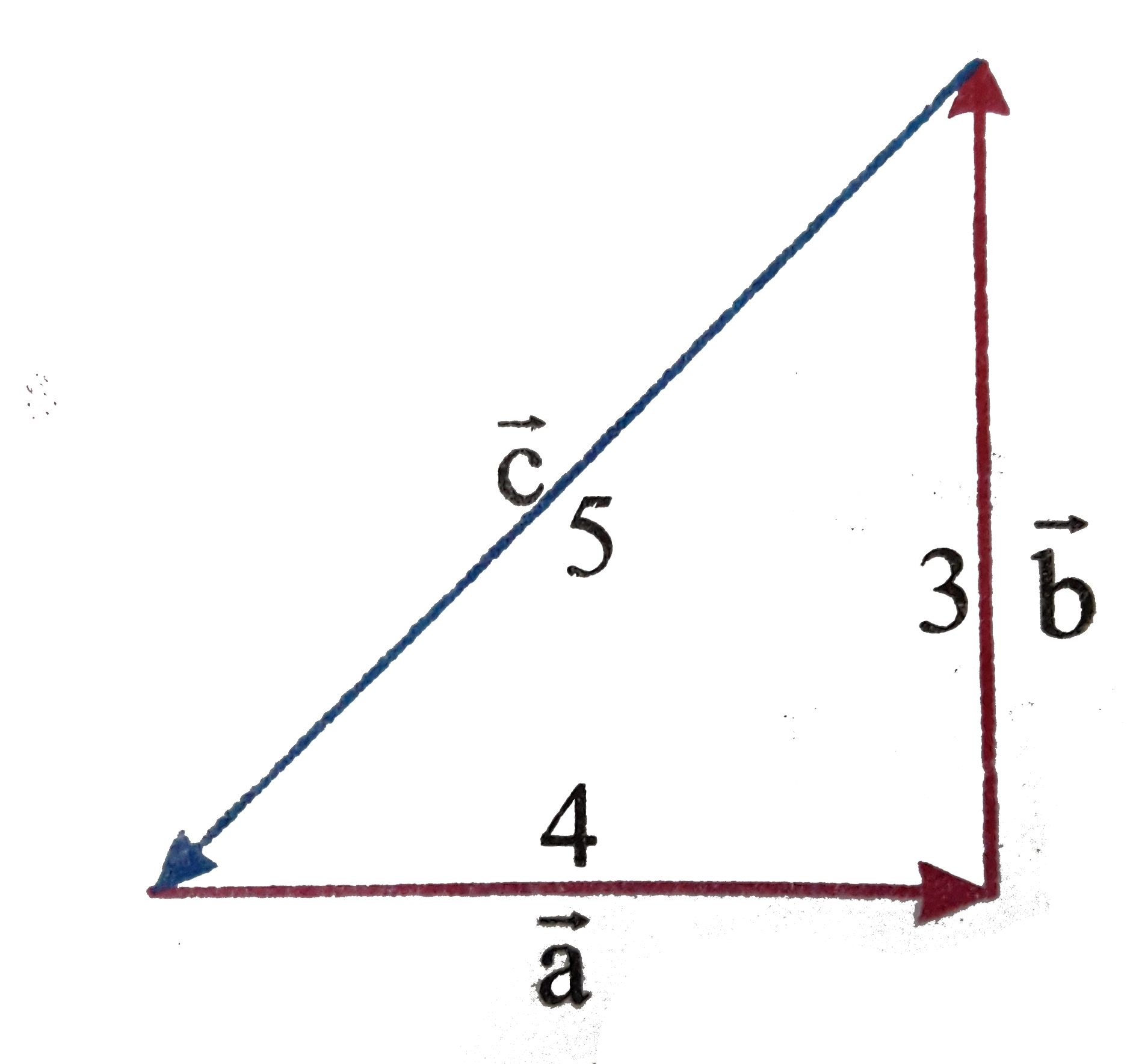 A−9B+9C0D−3
A−9B+9C0D−3
Three vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View SolutionThree vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →B
View SolutionThree vectors →A,→B and →C satisfy the relation →A.→B=0 and →A.→C=0. The vector →A is parallel to
View SolutionThree vectors →A,→B,→C are shown in the figure. Find angle between
(i) →A and →B (ii) →B and →C (iii) →A and →C.
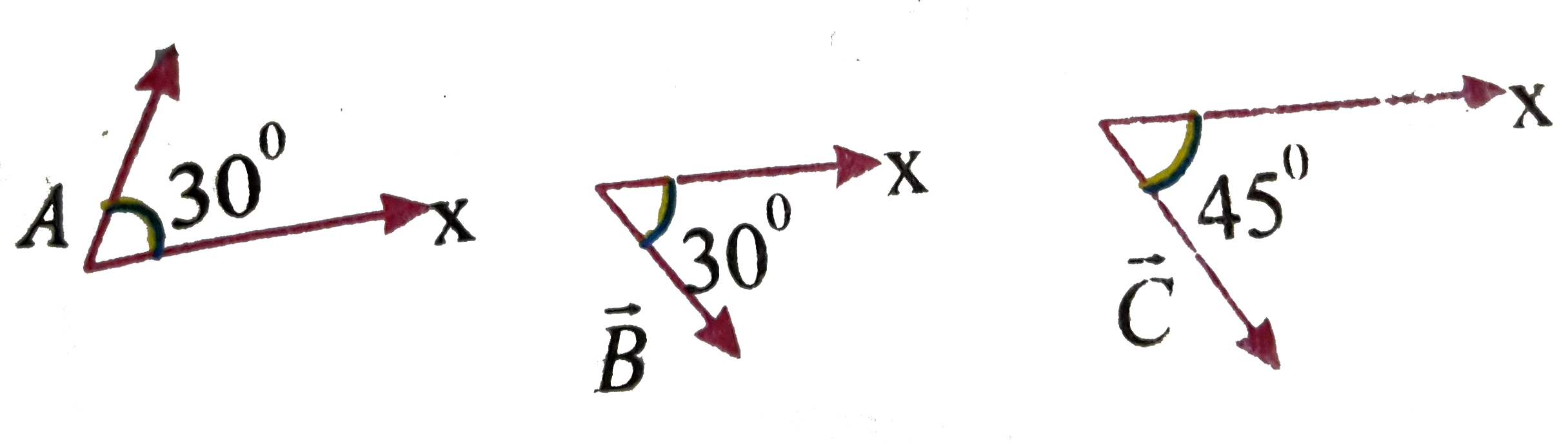
View SolutionThree vectors →A,→B and →C satisfy the relation →A.→B=0 and →A.→C=0. The vector →A is parallel to
View Solution
