A solid disc has a radius R. Density of its material Is given by ρ=ρ0(2−rR) where ρ0,is a constant and r is the radial distance measured from the centre. Then the moment of inertia of the disc about an axis passing through its centre and perpendicular to the plane of the disc is
27MR2
518MR2
9/20MR^2
7/12MR^2
The correct Answer is:C
Related Playlists
Similar Practice Problems
- Question 1 - Select One
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correct - Question 1 - Select One
The surface mass density of a disc of radius a varies with radial distance as σ=A+Br where A & B are positive constants then moment of inertia of the disc about an axis passing through its centre and perpendicular to the plane
A2πa4(A4+Ba5)B2πa4(Aa4+B5)Cπa4(A4+Ba5)D3πa4(A4+Ba5) - Question 1 - Select One
The moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
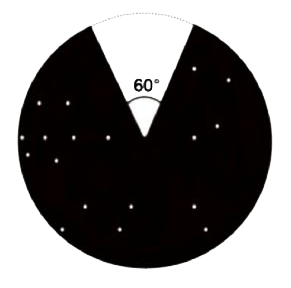 AMR22B7MR212C7MR26D5MR212
AMR22B7MR212C7MR26D5MR212
Similar Questions
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionThe surface mass density of a disc of radius a varies with radial distance as σ=A+Br where A & B are positive constants then moment of inertia of the disc about an axis passing through its centre and perpendicular to the plane
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :
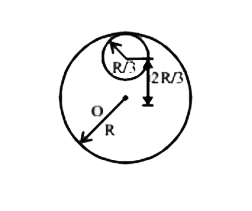 View Solution
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :
 View Solution
View SolutionA circular hole of radius r/2 is cut from a circular disc of radius 'r'. The disc lies in the xy plane. Determine the moment of inertia about an axis passing through the centre and perpendicular to the plane of the disc.
View SolutionSurface mass density of disc of mass m and radius R is Kr2. Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
View Solution

