A spherical body of radius R rolls on a horizontal surface with linear velocity v. Let L1 and L2 be the magnitudes of angular momentum of the body about centre of mass and point of contact P. Then
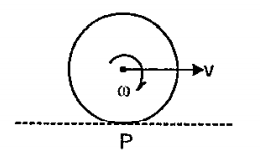
L2=2L1 if radius of gyration K = R
L2=2L1 for all cases
L2>2L1 if radius of gyration K<R
L2=2L1 if radius of gyration K>R
The correct Answer is:A, D
Topper's Solved these Questions
Similar Questions
A spherical body of radius R rolls on a horizontal surface with linear velociltly v. Let L1 and L2 be the magnitudes of angular momenta of the body about centre of mass and point of contact P. Then:
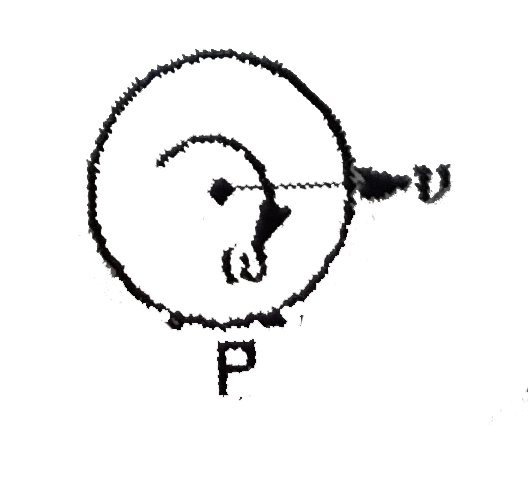
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View Solution
Knowledge Check
A spherical body of radius R rolls on a horizontal surface with linear velociltly v. Let L1 and L2 be the magnitudes of angular momenta of the body about centre of mass and point of contact P. Then:
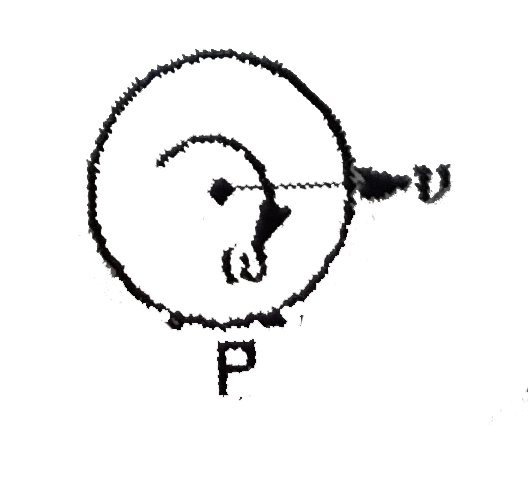 AL2=2L1 if radius of gyration K=RBL2=2L1 for all casesCL2>2L1 if radius of gyration K<RDL2>2L1 if radius of gyration K>R
AL2=2L1 if radius of gyration K=RBL2=2L1 for all casesCL2>2L1 if radius of gyration K<RDL2>2L1 if radius of gyration K>RA symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)A uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
 Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0
Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0
A thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.

View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionA disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :

View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View Solution
