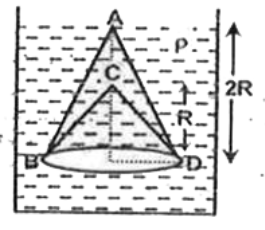
A solid con of uniform density and height 2R and base redius R has a conical portion scooped out form its base with the same base redius but height R as shown in the figure. The solid sone is floating in a liquid of density ρ with vertex A touching the fluid surface. If atmospheric pressure is P0 the force acting on the surface BCD due to liquid is
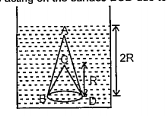
πR3ρg3[2+2P0Rρg]
πR3ρg3[5+3P0Rρg]
πR3ρg3[1+3P0Rρg]
πR3ρg3[4+3P0Rρg]
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
A solid cone of uniform density and height 2R and base radius R has a conical portion scooped out form its base with the same base radius but height R as shown in the figure. The solid cone is floating in a liquid of density ρ with vertex A touching the fluid surface . If atomospheric pressure is P0 the force acting on the surface BCD due to liquid is
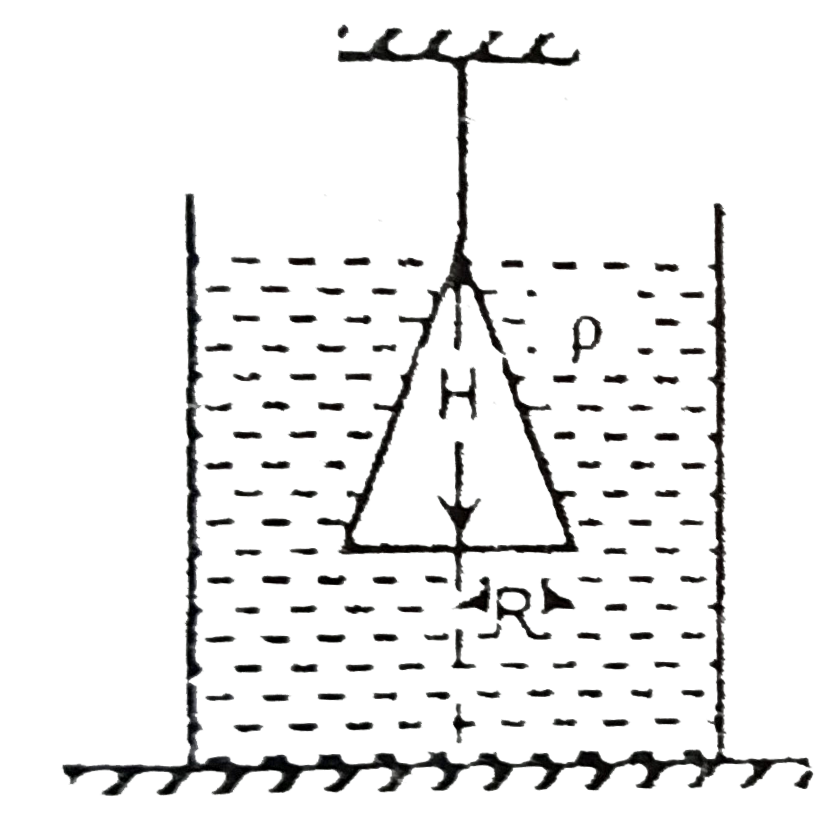
View SolutionA cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
View Solution
Knowledge Check
A cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
 AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2
AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2A triangular lamina of area A and height h is immersed in a liquid of density ρ in a vertical plane with its base on the surface of the liquid. The thrust on the lamina is.
A12AρghB13AρghC16AρghD23AρghA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceA∣∣2P0Rh+πR2ρgh−2RT∣∣B∣∣2P0Rh+Rρgh2−2RT∣∣C∣∣P0πR2+Rρgh2−2RT∣∣D∣∣P0πR2+Rρgh2−2RT∣∣
A conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

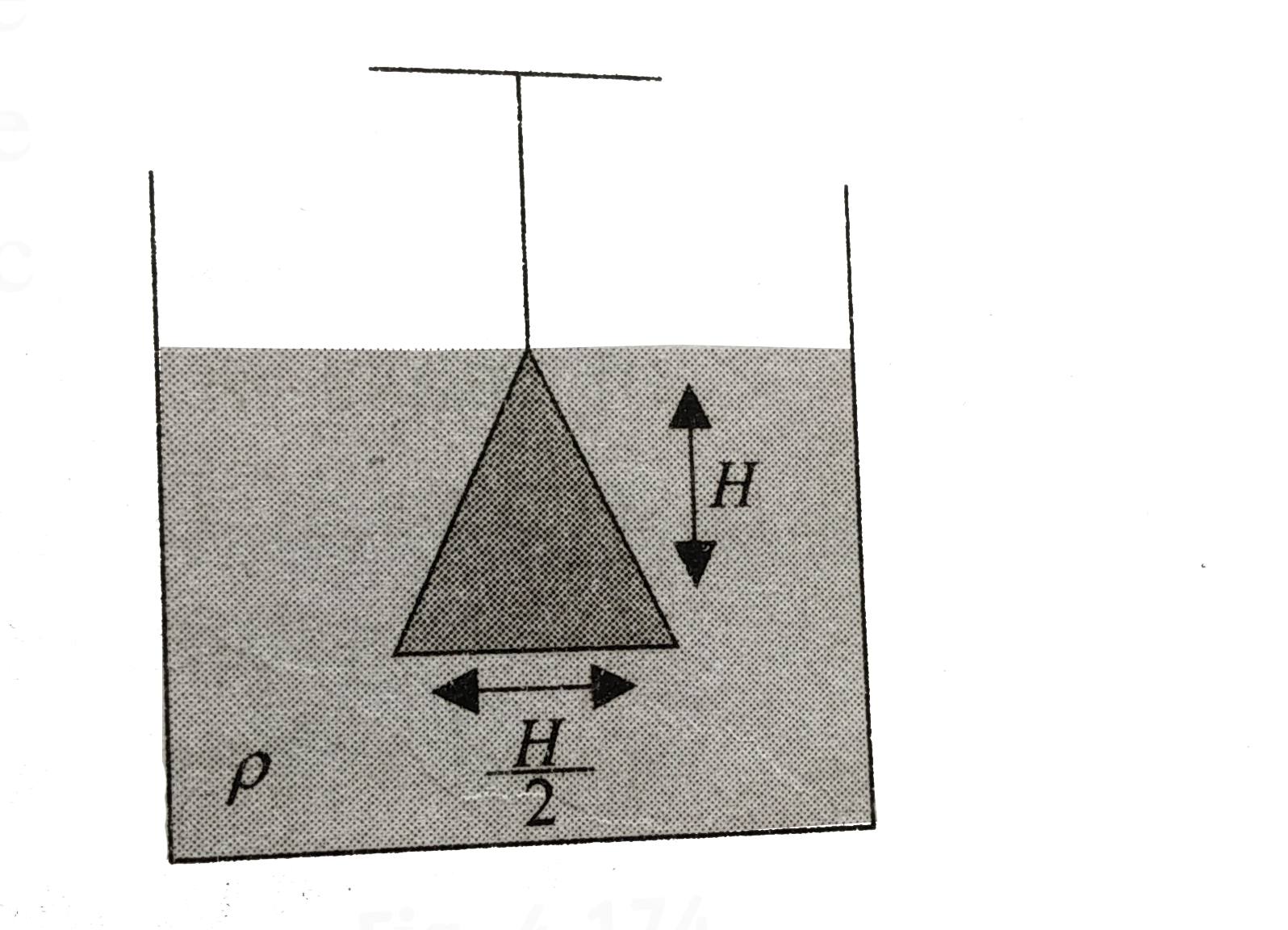
View SolutionA solid cone of height H and base radius H2 floats in a liquid of density ρ. It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is (P0= atmospheric pressure)
View SolutionA uniformly tapering vessel of height h whose lower and upper radii are r and R is completely filled with a liquid of density ρ The force that acts on the base of the vessel due of the liquid is
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

View SolutionA solid cone of height H and base radius H2 floats in a liquid of density ρ. It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is (P0= atmospheric pressure)

View Solution
