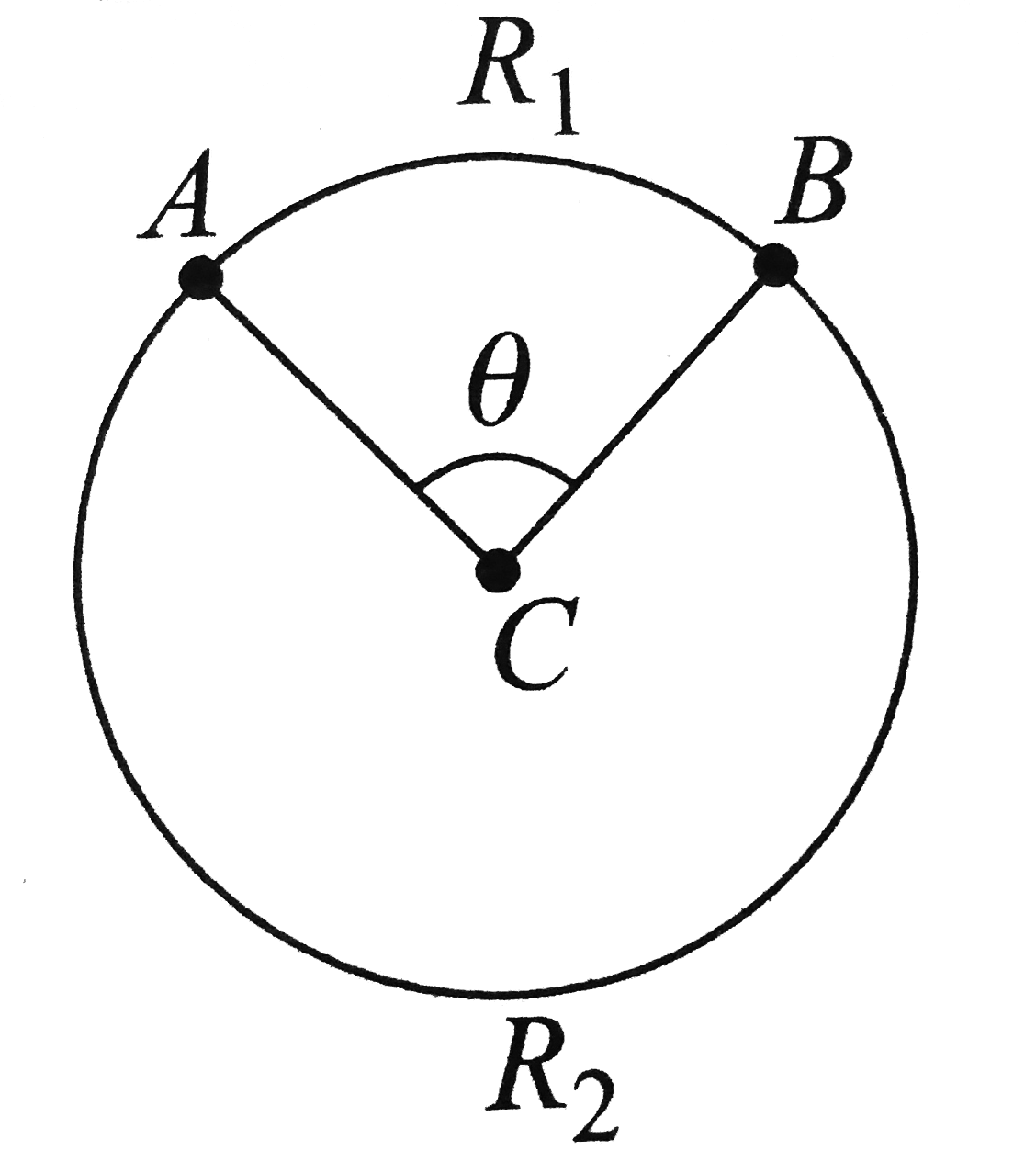
A and B are two points on a uniform metal ring (centre C) such that an

$A$ and $B$ are two points on uniform metal ring whose centre is $O$ The angle $A O B = θ$ A and $B$ are maintaind at two different constant temperatures When $θ = 180^{\circ}$ the rate of total heat flow from $A$ to $B$ is $1.2 W$ When $θ = 90^{\circ}$ this rate will be .
A $0.6$ watt
B $0.9$ watt
C $1.6$ watt
D $1.8$ watt
A uniform metal ring with centre $C$ have two points $A$ and $B$ such that angle $A C B$ is $θ$ . $A$ and $B$ are maintained at two different constant temperature.
If the angle between $A$ and $B$ i.e. $θ = 180^{\circ}$ the rate of heat flow from $A$ and $B$ is $1.2 W$ , then what will be the rate, when $θ = 90^{\circ}$ ?
A $0.6 W$
B $0.9 W$
C $1.6 W$
D $1.8 W$
$A$ and $B$ are two points on a uniform ring of resistance $R$ the $∠ A S C B = θ$ , whre $C$ is the centre of the sign. The equivalent reisrtance between $A$ and $b$
A $\frac{R}{4 π^{2}} (2 π - θ) θ$
B $R (I - \frac{θ}{2 π})$
C $R \frac{θ}{2 π}$
D $R \frac{2 π - θ}{4 π}$

A and B are two points on a uniform metal ring (centre C) such that $∠ A C B = θ$ . If the points A and B are maintained at different constant temperatures $(T_{A} > T_{B})$ , the rate of flow for $θ = 180^{\circ}$ is 1.2 W. If $θ$ is $90^{\circ} C$ , the rate of follow will be