Linear charge density of arc is λ and total angle α. Derive an expression for potential at centre
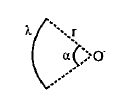 Solution in Bengali
Solution in Bengali
kλα
kλαr
12kλα
kλαr
Step by step video & image solution for Linear charge density of arc is lamda and total angle alpha. Derive an expression for potential at centre by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:PATHFINDERChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:QUESTION BANK
Explore 50 Videos
- MAGNETIC EFFECT OF CURRENT AND ELECTROMAGNETISM-I,II AND IIIBook:PATHFINDERChapter:MAGNETIC EFFECT OF CURRENT AND ELECTROMAGNETISM-I,II AND IIIExercise:QUESTION BANK
Explore 213 Videos
Similar Questions
Can two equipotential surfaces intersect?
View SolutionA wire placed along north south direction carries a current of 10A from south to north find the magnetic field due to a 1 cm piece of wire at a point 200cm north east from the piece
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is lamda
View SolutionA thread having linear charge density λ is in the shape of a circular arc of radius R subtending an angle θ at the centre.
(a). Find the electric field at the centre.
(b). Using the epression obtained in part (a) find the field at the centre if the thread were emicircular
(c). Find the field at centre using the expression obtained in part (a) for the case θ→0. Is the result justified?
(d). A thread having total charge Q (uniformly distributed is in the shape of a circular arc of radius R subtending an angle θ at centre. write the expression for the field at the center. Obtain the field whenθ→0. Make sure you understand the difference in case. (c) and (d).
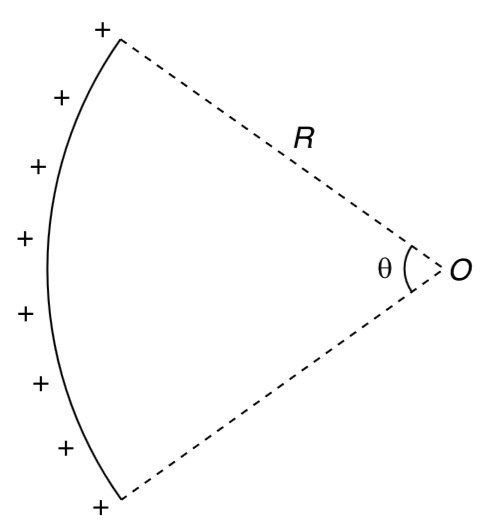
View SolutionAn arc of radius r carries charge. The linear density of charge is lamda and the arc subtends an angle (pi)/(3) at the centre.
View Solutionरेखीये आवेश घनत्व से क्या तात्पर्य है? गाउस के नियम का उपयोग करके एक आवेशित लम्बे तार के निकट, जिसका रेखीये आवेश घनत्व λ कुलोम/मीटर है, वैधुत क्षेत्र की तीव्रता के लिए व्यंजक व्युपानं कीजिए।
View SolutionDerive an expression for the electric potential due to a point charge.
View SolutionFind the electric field and potential at the centre of curvature of a uniformly charged semicircular rod of radius R with a total charge Q in SI. lambda is the linear charge density.
View SolutionFind the gravitational field strength and potential at the centre of arc of linear mass density lambda subtending an angle 2alpha at the centre.
View SolutionFind the total force on charge q due to a charge rod having linear charge density lamda C/m placed as shown in figure.
View Solution(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
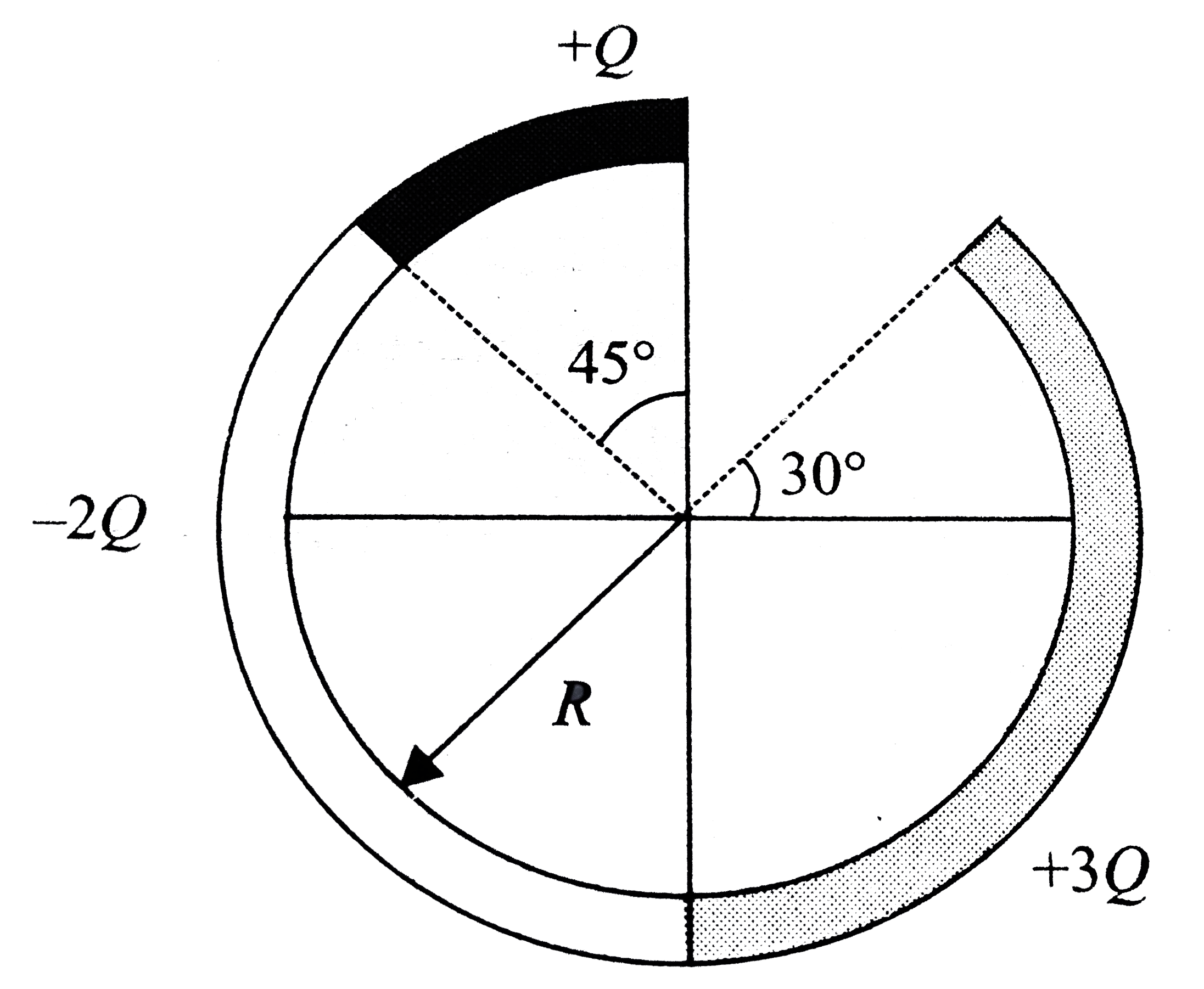 .
.
View Solutionएक अर्द्धवृत्तीय चाप, जिसकी त्रिज्या a है, को आवेशित किया गया। रेखीय आवेश घनत्व λ है, तो चाप के केन्द्र पर वैद्युत क्षेत्र की तीव्रता का मान होगा
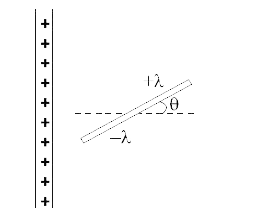
View Solutionएक बड़ी पटिका का समरूप पृष्ठ आवेश घनत्व σ है। 2l लम्बाई की एक छड़ पर आधे भाग पर रेखीय आवेश घनत्व λ एक दूसरे आधे भाग पर रेखीय आवेश घनत्व −λ है। छड़ मध्य बिन्दु O पर किलकित है एवं पट्टिका के अभिलम्ब से θ कोण पर है। छड़ पर बलाघूर्ण होगा।
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is lamda
View SolutionAn arc of radius r carries charge. The linear density of charge is λ and the arc subtends an angle π3 at the centre.
View Solution