The normal to the curve x=a(cosθ+θsinθ),y=a(sinθ−θcosθ) at any point θ is such thatSolution in Bengali
it passes through the origin
it makes an angle π2+θ with the x-axis
it passes through (aπ2,−a)
it is at a constant distance from the origin
The correct Answer is:D
Step by step video, text & image solution for The normal to the curve x=a(costheta+thetasintheta),y=a(sintheta-thetacostheta) at any point theta is such that by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
The distance S metres moved by a particle traveling in a straight line in t second is given by S = 45t+11t2−t3. Find the time when the particle comes to rest.
01:29View SolutionFind dydx , if x=a(cosθ+θsinθ) , y=a(sinθ−θcosθ)
03:50View Solutionवक्र x=cosθ,y=sinθ के बिंदु θ पर अभिलम्ब का समीकरण ज्ञात कीजिये
05:49View Solutionयदि (If) x=a(cosθ+θsinθ),y=a(sinθ−θcosθ), find dydx.
02:53View Solutionयदि x=a(cosθ+θsinθ),y=a(sinθ−θcosθ)तबdydx=
02:41View Solutionवक्र x=a(cosθ+θsinθ) और y=a(sinθ−θcosθ) पर विचार कीजिए ।
dydx किसके बराबर है ?03:06View Solutionवक्र x=a(cosθ+θsinθ) और y=a(sinθ−θcosθ) पर विचार कीजिए ।
d2ydx2 किसके बराबर है ?02:03View SolutionIf x=a(cosθ+θsinθ),y=a(sinθ−θcosθ), then dydx=
04:54View SolutionIf x=sinθ+θcosθ,y=cosθ−θsinθ, then (dydx) at θ=π2 is
05:46View SolutionThe normal to he curve x=a(cosθ+θsinθ),y=a(sinθ−θcosθ) at any point 'θ' is such that
02:41View SolutionFindy2 in each of the following cases:
x=a(cosθ+θsinθ),y=a(sinθ−θcosθ)atθ=π404:43View Solutiona, b, c এর মান নির্ণয় করো।
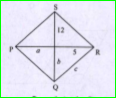03:13View Solutionনিম্নলিখিত প্রতিক্ষেত্রে y2 এর মান নির্ণয় করো : x=a(cosθ+θsinθ),y=a(sinθ−θcosθ) যখন θ=(π4)
12:01View SolutionShow that the normal at any point θ to the curve x=acosθ+aθsinθ,y=asinθ–aθcosθ is at a constant distance from the origin.
09:01View SolutionShow that the normal at any point θ to the curve x = a costheta + a theta sin theta, y = a sintheta – atheta costheta is at a constant distance from the origin.
09:44View SolutionShow that the normal at any point θ to the curve x=acosθ+aθsinθ,y=asinθ–aθcosθ is at a constant distance from the origin.
02:51View Solution