Let In=∫π40tannxdx, then 1I2+I4,1I3+I5,1I4+I6,1I5+I7 Solution in Bengali
44200
44198
44204
none of these
The correct Answer is:A
Step by step video, text & image solution for Let I_n=int_0^(pi/4)tan^nxdx, then 1/(I_2+I_4),1/(I_3+I_5), 1/(I_4+I_6), 1/(I_5+I_7) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If f(x) =|x-2|+1, evaluat Ltx→2+f(x)−f(2)x−2 and Ltx→2−f(x)−f(2)x−2. What can you say about the existence of f'(x) at x=2?
View SolutionIf ∣∣∣x−2−33x2x∣∣∣=3, Find the integral value of x.
View SolutionIn the given circuit diagram, the currents, I1=−0.3A,I4=0.8A and I5=0.4A, are flowing as shown. The currents I2,I3 and I6 respectively, are :
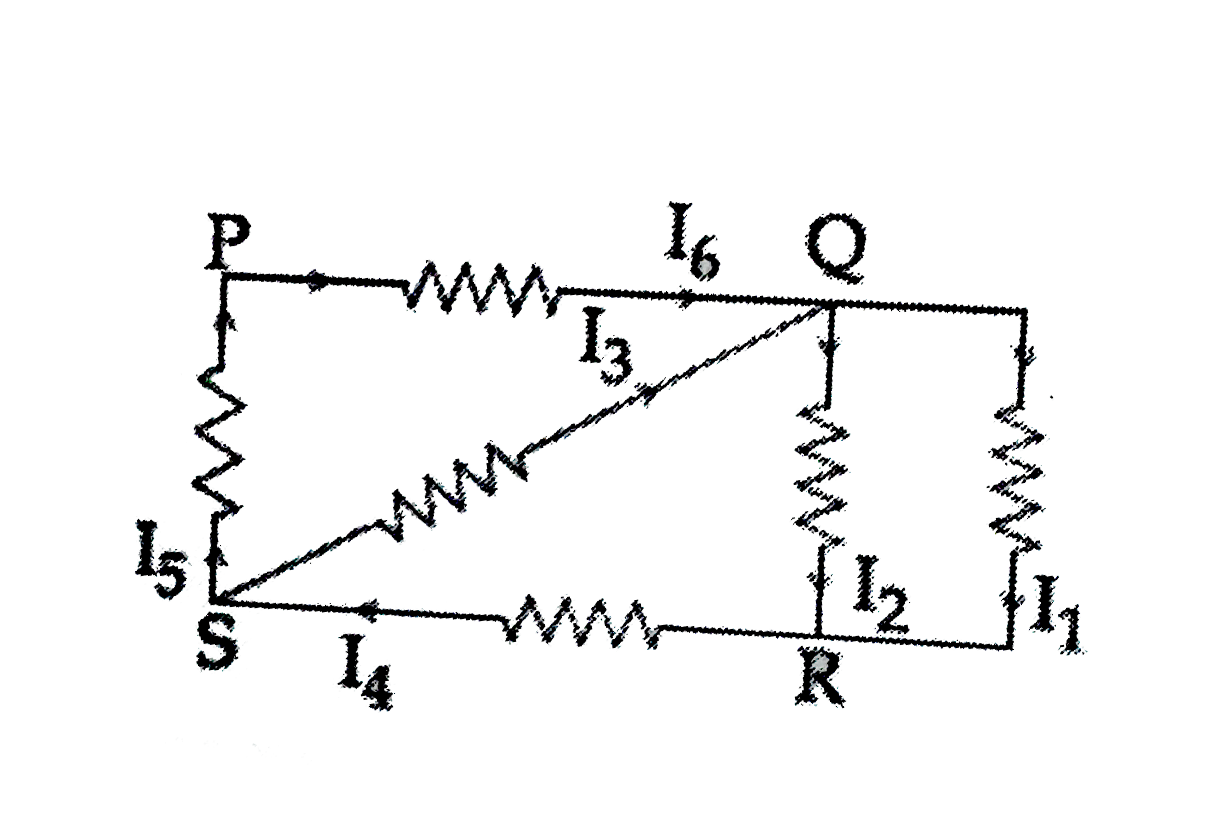
View SolutionIn the given circuit diagram, the currents, I1=−0.3A,I4=0.8A and I5=0.4A, are flowing as shown. The currents I2,I3 and I6 respectively, are :
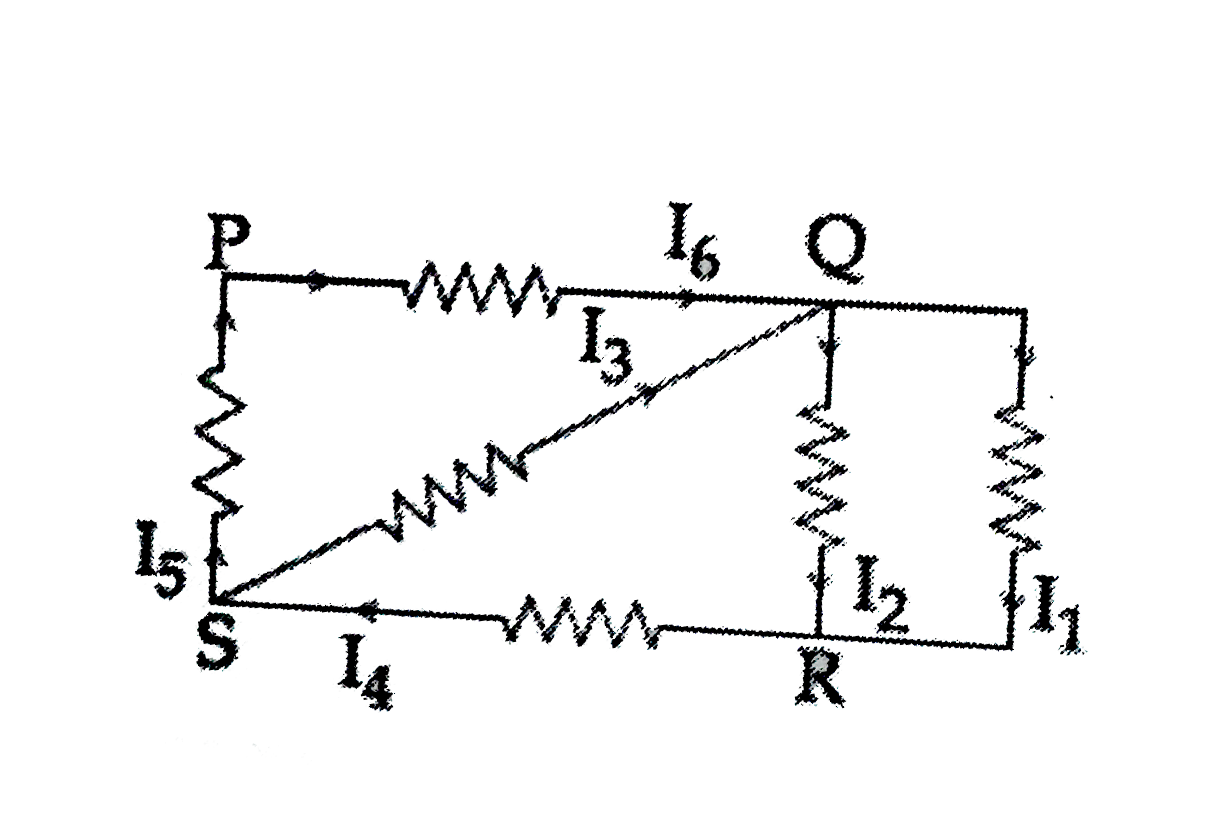
View SolutionFind relation in between current i_1,i_2,i_3,i_4,i_5 and i_6.
View SolutionIf In=∫π/20tannxdx, then I2+I4,I3+I5,I4+I6,…., are in
View SolutionIn=∫π40tannxdx হলে (I7+I5)-এর মান হবে–
View SolutionI1=∫π20sinx−cosx1+sinxcosxdx,I2=∫2π0cos6xdx,I3=∫π2π2sin3xdx,I4=∫101n(1x−1)dx.Then I2=I3=I4=0,I1≠0 I1=I2=I3=0,I4≠0 I1=I2=I3=0,I4≠0 I1=I4=I3=0,I2≠0
View SolutionIfI1=∫102x^2,I2=∫102x^3dx,I3=∫21^x2dx,I4=∫212x^3dx, then which of the following is/are ture?
a) I1>I2
(b) I2>I2
c)I3>I4
(d) I3<I4
View SolutionIf In=∫π/40tannxdx , show that 1I2+I4,1I3+I5,1I4+I6,1I5+I7, form an A.P. Find the common difference of this progression.
View SolutionIn the given circuit diagram, the currents, I_1=-0.3A,I_4=0.8A and I_5=0.4A , are flowing as shown. The currents I_2,I_3 and I_6 respectively, are :
View SolutionSix wires of current I1=1A,I2=2A,I3=3A,I4=1A,I5=5A and I6=4A cut the page perpendicularly at the points 1, 2,3,4,5 and 6. respectively as shown in the figure . Find the value of the integral ∮→B.d→1 around the closed path.

View SolutionIn=∫π/2π/4Cotnx⋅dx Find relation between I2+I4,I3+I5,I4+I6,
View SolutionLet In=∫π40tannxdx, then 1I2+I4,1I3+I5,1I4+I6,1I5+I7
View SolutionLet In=∫nπ0sinx1+xdx n = 1,2,3,4. Arrange I1,I2,I3,I4 in increasing order of magnitude.
View Solution
