If →OA=i−j and →OB=j−k, the unit vector perpendicular to the plane AOB isSolution in Kannada
1√I+j−k
1√3(i+j+k)
1√i−j−k
none of these
The correct Answer is:B
Step by step video, text & image solution for If vec OA = i-j and vec OB = j-k, the unit vector perpendicular to the plane AOB is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The direction cosines of the line making angles 45o,30o and 120o with the coordinate axes are
View SolutionVector of length of 3 unit which is perpendicular to vec i + vec j + vec k and lies in the plane of vec i + vec j + vec k and 2vec i-3vec j, is (1) (3) / (sqrt ( 6)) (vec i-2vec j + vec k) (2) (3) / (sqrt (6)) (2vec i-vec j-vec k) (3) (3) / (sqrt (114)) ( 8vec i-7vec j-vec k) (4) (3) / (sqrt (114)) (- 7vec i + 8vec j-vec k)
View SolutionFind a unit vector perpendicular to both of the vectors →a+→b and →a−→b where →a=ˆi+ˆj+ˆk,→b=ˆi+2ˆj+3ˆk.
View Solutionvec OA=hat i+3hat j-2hat k and vec OB=3hat i+hat j-2hat k Then vector vec OC biecting the angle AOB and C being a point on the line AB is
View SolutionFind vec a unit vector perpendicular to each of the vectors vec a=3i+2j-3k and vec b=i+j-k
View SolutionIf vec OA=3hat i+hat j-2hat k and vec OB=5hat i+4hat j+hat k then find the value of vec AB
View Solutionयदि →A=2ˆi+2ˆj+ˆk तथा →B=2ˆi−2ˆj+3ˆk हो तो →A व →B के लंबवत (i) एकांक सदिश (ii) 8 मात्रक परिमाण का सदिश ज्ञात कीजिये ।
View Solutionयदि −−→OA=2→i+5→j−2→kतथा −−→OB=3→i+6→j+5→k तो −−→AB=
View Solutionयदि −−→OA=2→i−→j+→k,−−→OB=→i−3→j−5→k और −−→OC=3→i−4→j−4→k तो सिद्ध करें की
−−→OA.−−→OB=0
View SolutionIf −−→OA=ˆi−2ˆk and −−→OB=3ˆi−2ˆj then the direction cosines of the vector −−→AB are -
View Solutionयदि −−→OA=4ˆi−3ˆj+5ˆk,−−→OB=7ˆi−5ˆj−ˆk,−−→OC=−2ˆi+ˆj+3ˆk,−−→OD=3ˆi+2ˆj+5ˆk तब सदिश −−→AB पर −−→CD सदिश का प्रक्षेप ज्ञात कीजिए।
View SolutionThe resultant of vectors −−→OAand−−→OB is perpendicular to −−→OA. Find the angle AOB.
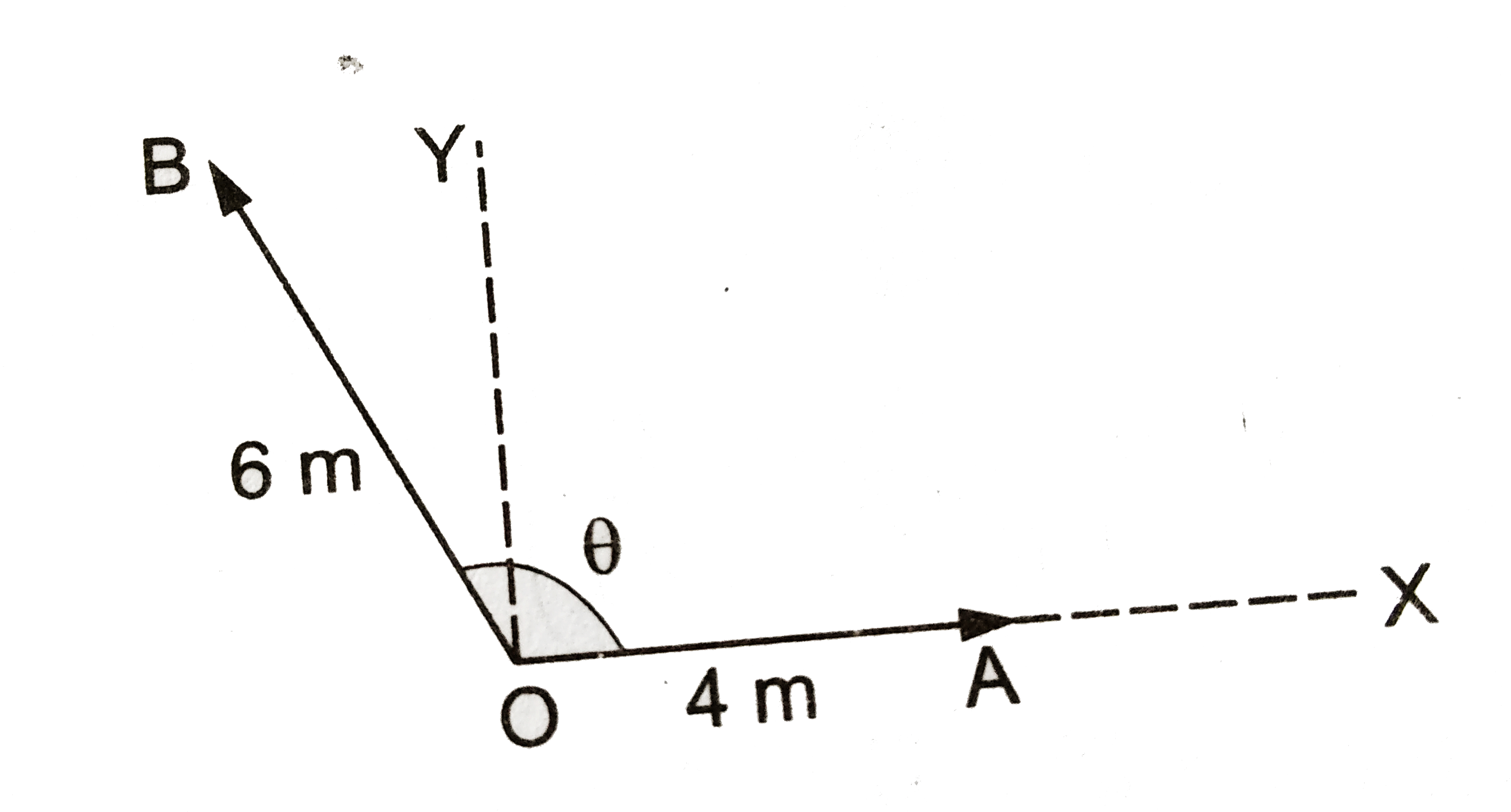
View SolutionThe unit vector perpendicular to vectors →i−→jand→i+→j forming a right handed system is
View SolutionA vector →c perpendicular to the vectors 2→i+3→j−→kand→i−2→j+3→k satisfying →c.(2→i−→j+→k)=−6 is
View SolutionIf →a=−i+j+k,→b=i−j+k, then a unit vector perpendicular to →a and →b is
View Solution
