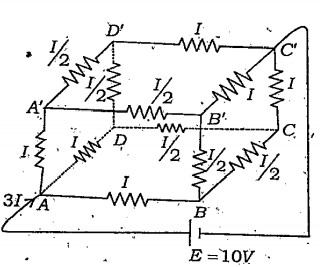
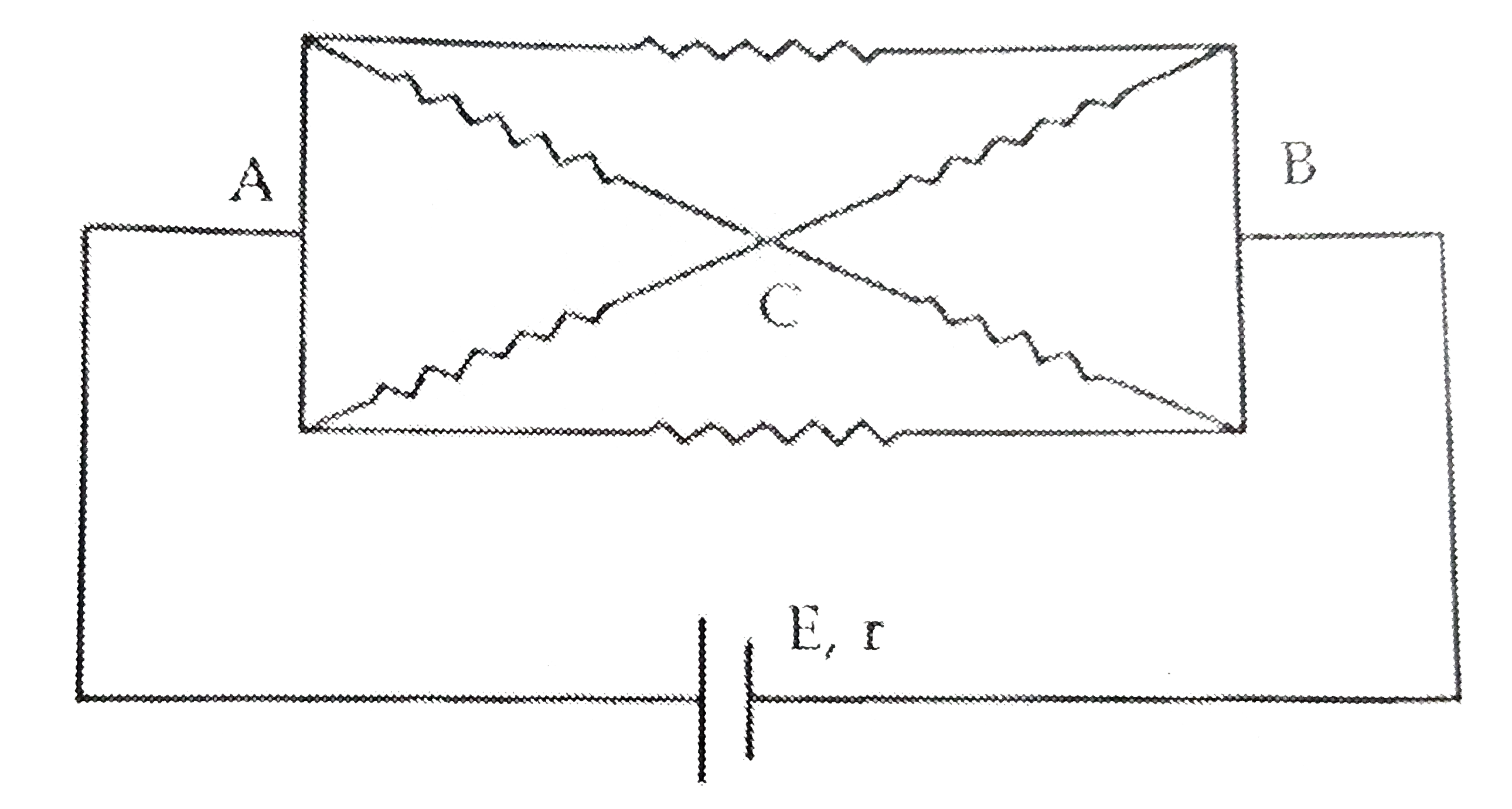
(Attempt any three of the following questions) State Kirchhoff's (i) Junction rule and (ii)Loop rule. Determine the equivalent resistance of the network given below and the total current going out of the battery. Given, each resistor has resistance of 1ω.
 Solution in Assamese
Solution in Assamese
Step by step video & image solution for (Attempt any three of the following questions) State Kirchhoff's (i) Junction rule and (ii)Loop rule. Determine the equivalent resistance of the network given below and the total current going out of the battery. Given, each resistor has resistance of 1omega. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
β of a given transistor is 99. What is the value of α?
View SolutionWhat is Curie temperature of a ferromagnetic material? Give one example of a ferromagnetic material.
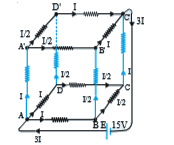
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω 22. Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionState Kirchhoff's rules . Apply Kirchhoff's rules to the loops ACBPA and ACBQA to write the expressions for the currents I_(1) , I_(2) and I_(3) in the network .
View SolutionState Kirchhoff's junction rule.
View SolutionA network of resistors is connected to a 5 V battery with internal resistance of 1Omega as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops V_(BC) and V_(CD)
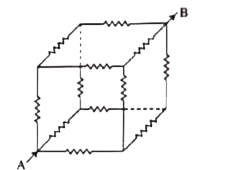
View SolutionEach resistance is the given cubical network has resistance of 1Ω and equivalent resistance between A and B is .
View SolutionIn the given network of resistors, each of resistance R, calculate the equivalent resistance between the junctions A and E
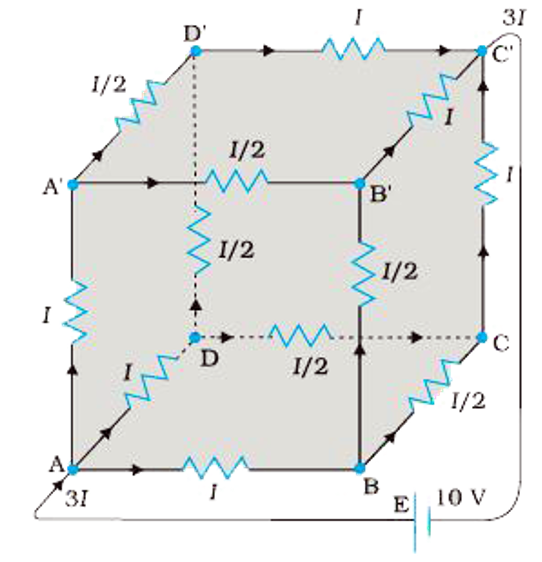
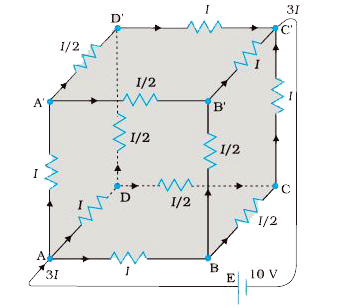
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
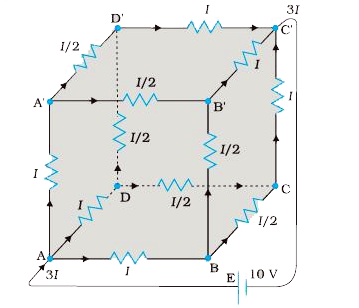
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionState Kirchhoff's rules of current distribution in an electrical network. Using these rules determine the value of the current I1 in the electric circuit of Fig.
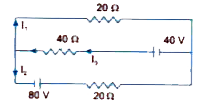
View SolutionState Kirchhoff's rules of current distribution in an electrical network. Using these rules determine the value of the current I1 in the electric circuit of Fig.
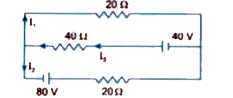
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω Determine the equivalent resistance of the network and the current along each edge of the cube.
View Solution(i) State the two Kirchhoff's laws, Explain of the briefly how these rules are justified.
(ii) The current is drawn from a cell of emf E andinternal resistance r connected to the network of resistors each of resistance r as shown in the figure. Obtain the expression for (i) The current draw from the cell and (ii) the power consumed in the network .
View SolutionA network of Resistors is Connected to a 16V battery with internal resistance 1Omega as shown in Figure below. (a) Compute the equivalent resistance of the network (b) Calculate the total current in the circuit
View SolutionDetermine the current drawn from a 12V supply with interna! resistance 0.5Omega by the infinite network shown in Fig Each resistor has 1Omega resistance.
View Solution
