A small ball A is.thrown up with a velocity 40ms from the ground. Another identical ball B of same mass is just dropped from a height of 50m simultaneously at time t=0 so that both collide in air and stick together. Find the value of t (in s) at which combined mass will fall to the ground. (g=10m(s)2)
'(##CEN_KSR_PHY_JEE_C08_E01_023_Q15##)'
The correct Answer is:5
Topper's Solved these Questions
Similar Questions
A sphere A is thrown up with velocity 20m/sec from the ground. Sphere B of same mass is dropped from a height of 80 m simultaneously, at time t = 0 so that both collide in air and stick together. Find the time (in second) after which the combined mass will fall on the ground. (Calculate from t = 0)(g=10m/sec2)
View SolutionA sphere A is thrown up with velocity 20m/sec from the ground. Sphere B of same mass is dropped from a height of 80 m simultaneously, at time t = 0 so that both collide in air and stick together. Find the time (in second) after which the combined mass will fall on the ground. (Calculate from t = 0)(g=10m/sec2)

View Solution
Knowledge Check
A ball is thrown from the ground with a velocity of 20√3 m/s making an angle of 60∘ with the horizontal. The ball will be at a height of 40 m from the ground after a time t equal to (g=10ms−2)
A√2 secB√3 secC2 secD3 sec
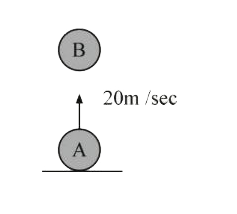
Two identiacal masses are as shown in figure. One is thrown upwards with velocity 20 m/s and another is just dropped simultaneously.
The masses collide I air and stick together. After how much time the combined mass will fall to the gorund (calculate the time from the starting when the motion was started )
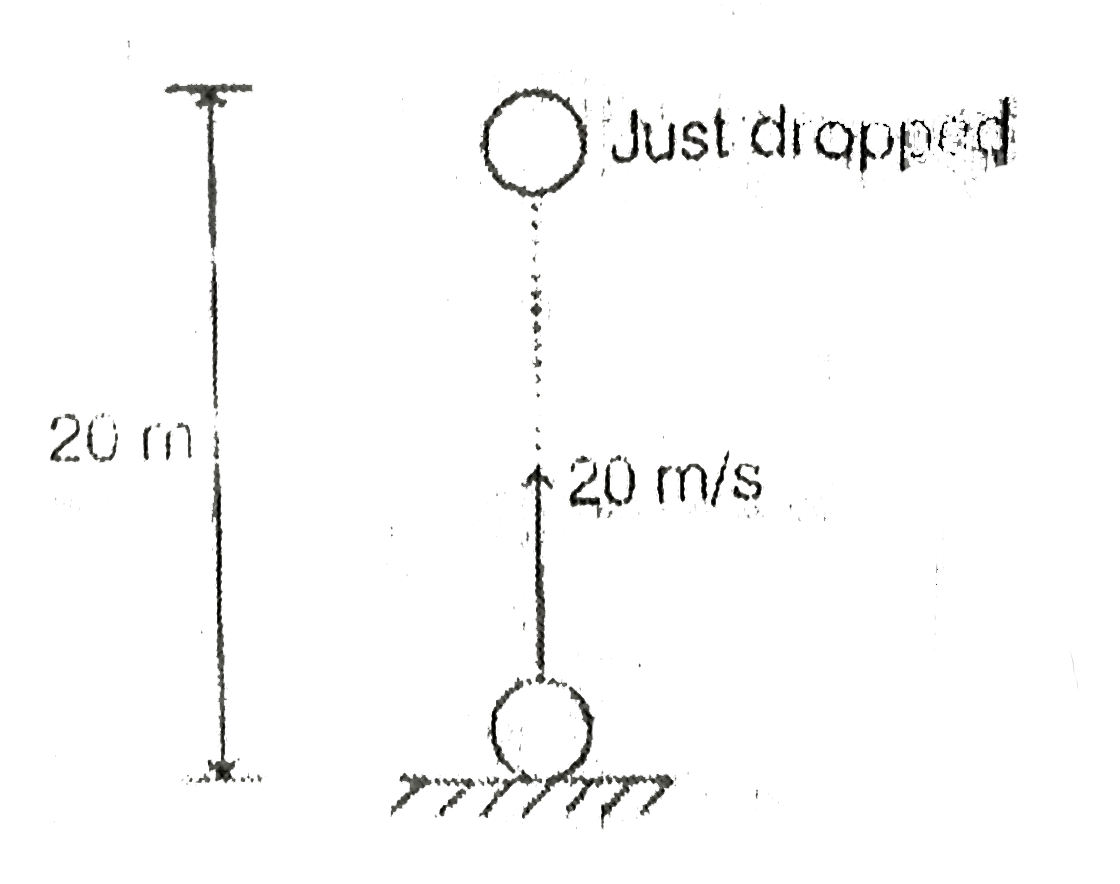
View SolutionTwo identiacal masses are as shown in figure. One is thrown upwards with velocity 20 m/s and another is just dropped simultaneously.
The masses collide I air and stick together. After how much time the combined mass will fall to the gorund (calculate the time from the starting when the motion was started )
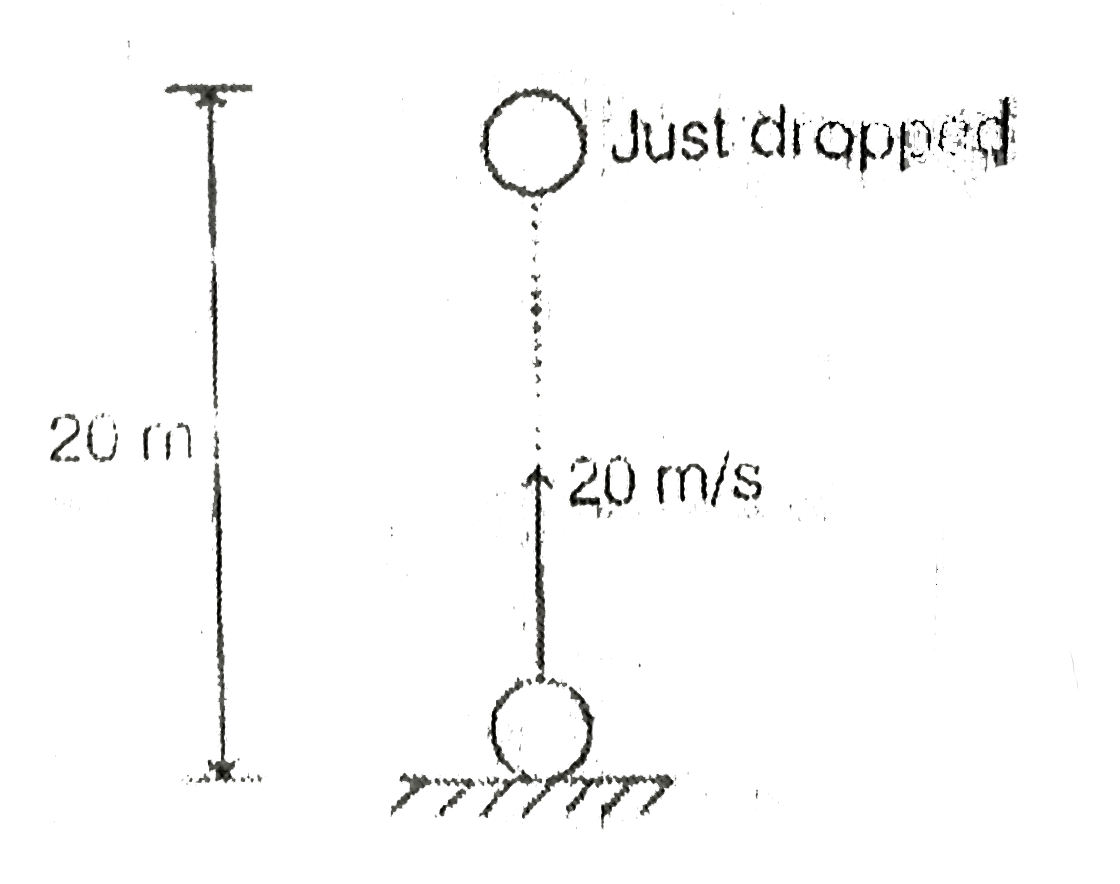
View SolutionA ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. The relative speed of the balls varies with time as
View SolutionA ball 'A' is thrown upwards from ground level with a velocity of 20ms−1. Another ball 'B' is thrown downwards from a height of 40 m with the same speed. Find the height at which the two balls meet (take g=10ms−2).
View SolutionA ball is dropped from a balloon rising up with a velocity of 50 m/s. When the ball is dropped the balloon was at a height of 100 m. Find the time taken by the ball to reach the ground.
View SolutionA ball is thrown from the top of a building with a velocity of 10 m/s and returns with a velocity of 30 m/s to the ground. Find the height of the building.
View SolutionA ball is thrown up at a speed of 4.0 m/s. Find the maximum height reached by the ball. Take g=10m/s2.
View Solution
