In an ac dynamo, the peak value of emf is 60V. The induced emf (in V) in the position when the armature makes an angle of 30∘ with the magnetic ficld perpendicular to the coil, will be
The correct Answer is:30
To find the induced emf in an AC dynamo when the armature makes an angle of 30∘ with the magnetic field, we can follow these steps:
Step 1: Understand the relationship between peak emf and induced emf
The peak value of the induced emf (E0) is given as 60V. The induced emf at any angle can be calculated using the formula:
E=E0sin(θ)
where:
- E is the induced emf,
- E0 is the peak value of the emf,
- θ is the angle between the magnetic field and the normal to the coil.
Step 2: Identify the angle
In this case, the angle θ is given as 30∘.
Step 3: Substitute the values into the formula
Now we can substitute the known values into the formula:
E=60sin(30∘)
Step 4: Calculate sin(30∘)
We know that:
sin(30∘)=12
Step 5: Compute the induced emf
Now, substituting sin(30∘) into the equation:
E=60×12=30V
Conclusion
Thus, the induced emf when the armature makes an angle of 30∘ with the magnetic field is 30V.
---
The peak value of the induced emf (E0) is given as 60V. The induced emf at any angle can be calculated using the formula:
E=E0sin(θ)
where:
- E is the induced emf,
- E0 is the peak value of the emf,
- θ is the angle between the magnetic field and the normal to the coil.
In this case, the angle θ is given as 30∘.
Now we can substitute the known values into the formula:
E=60sin(30∘)
We know that:
sin(30∘)=12
Now, substituting sin(30∘) into the equation:
E=60×12=30V
Thus, the induced emf when the armature makes an angle of 30∘ with the magnetic field is 30V.
Topper's Solved these Questions
Similar Questions
In an ac dynamo, the peak value of emf is 60V. The induced emf (in V) in the position when the armature makes an angle of 30∘ with the magnetic ficld perpendicular to the coil, will be
View SolutionFind the emf induced in the coil shown in figure.The magnetic field is perpendicular to the plane of the coil and is constant.
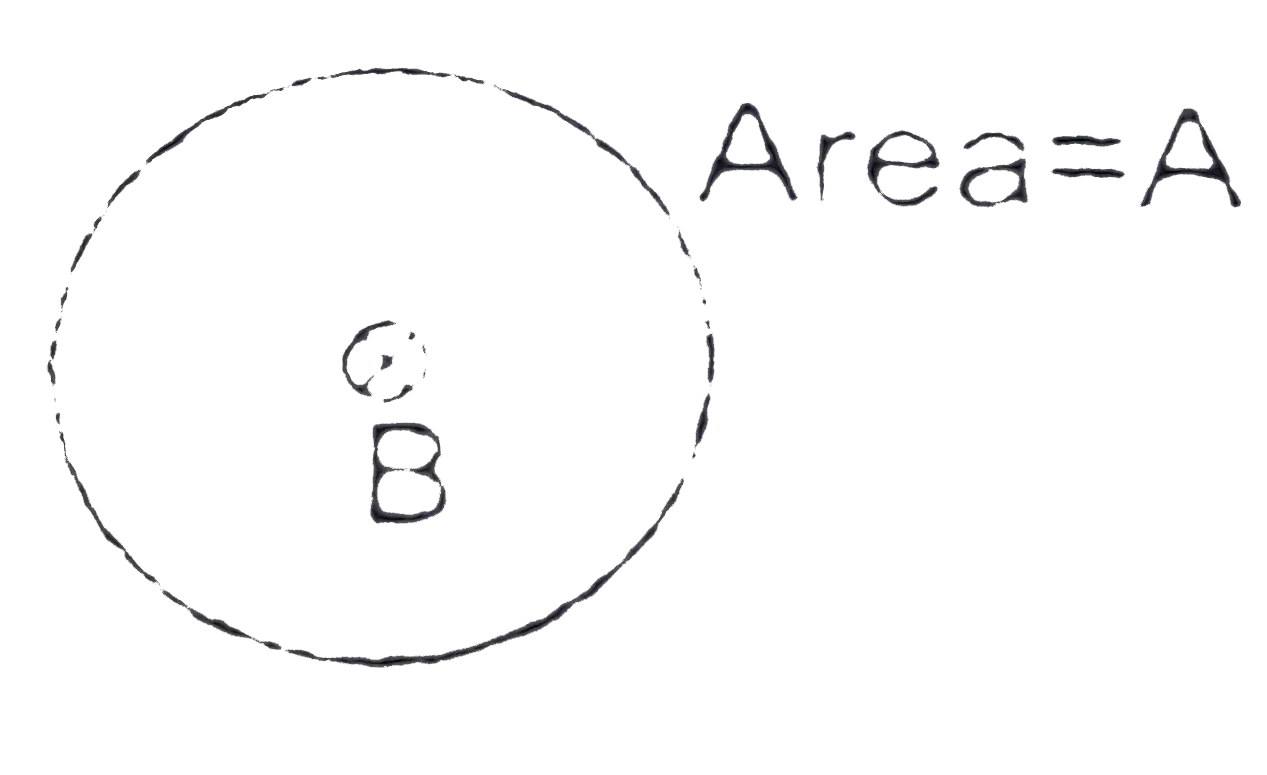
View Solution
Knowledge Check
The induced e.m.f. in a rod of length l translating at a speed v making an angle θ with length l and perpendicular to magnetic field B is
AB/vBB/v cosθCB/v sinθDB/v tanθA rectangular coil rotates about an axis normal to the magnetic field, If Em is the maximum value of the induced emf, then the instantaneous emf when plane of the coil makes an angle of 45∘ with the magnetic field is
A12EmB14EmC1√2EmDEmBy a change of current from 5 A to 10 A in 0.1 s, the self induced emf is 10 V. The change in the energy of the magnetic field of a coil will be
A5JB6JC7.5JD9J
Find the emf induced in the coil shown in figure. The magnetic field is perpendicular to the plane of the coil and is constant.
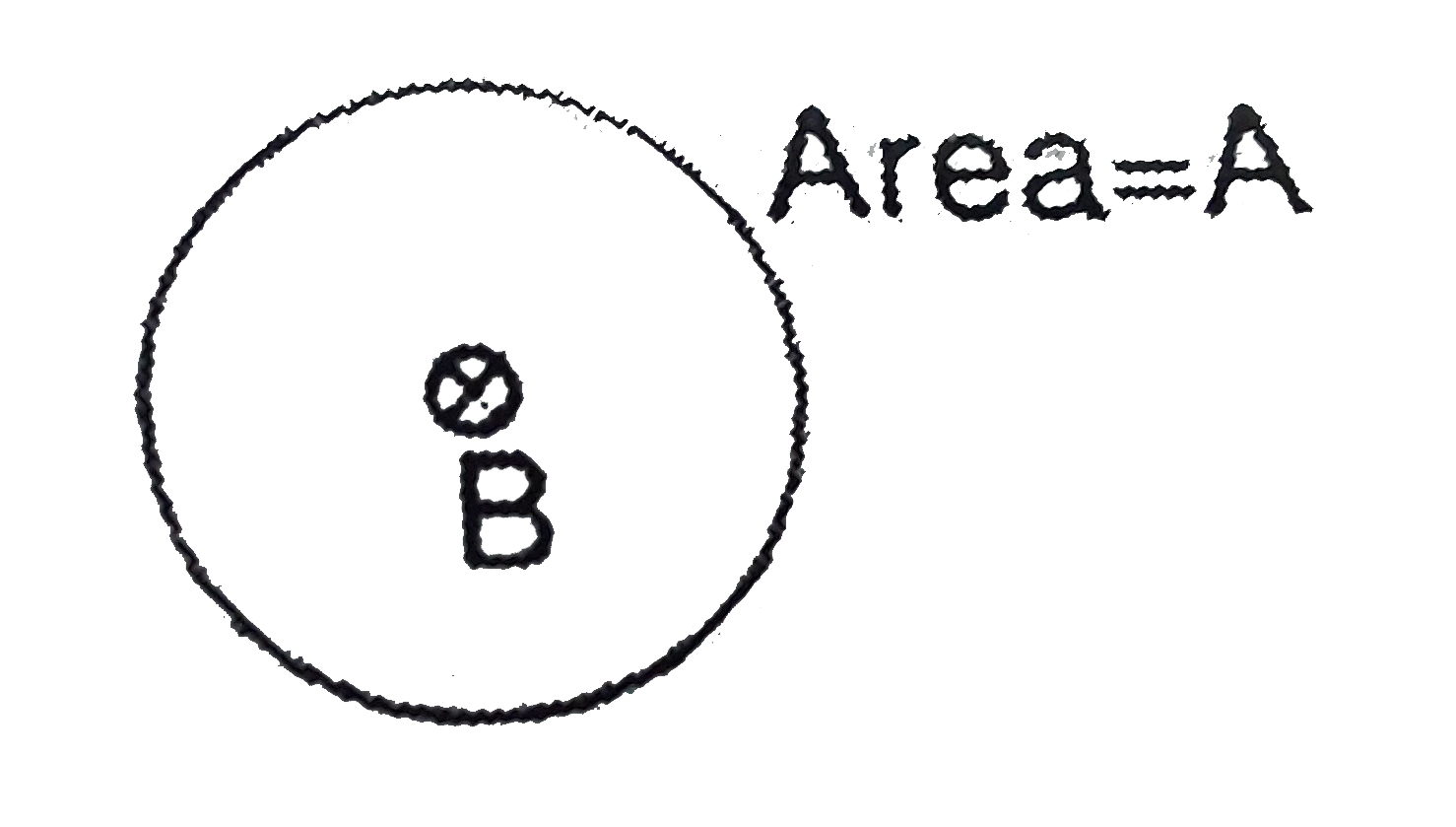
View SolutionWhat is the instantaneous value of induced emf generated in the coil of AC generator ?
View SolutionAt which position of the plane of the rotating coil with the direction of magnetic field the e.m.f induced in the coil is maximum ?
View SolutionIf the peak value of an alternating emf is 15V, what is its mean value over half cycle?
View SolutionThe v-t graphs of two objects make angles of 30∘ and 60∘ with the time-axis. Find the ratio of their accelerations.
View Solution
