A square wire of length L1 mass m and resistance R slides without friction on parallel conducting resistanceless rails. The rails are interconinected at the bottom by resistanceless rails so that the wire and the rails form a closed rectangular loop. The plane of the rails is inclined at an angle θ with the horizontal and a vertical uniform magnetic field B exists within the frame. If the wire acquires a steady velocity of magnitude v=kmgRsinθ6B2l2, cos2θ
'(##CEN_KSR_PHY_JEE_CO23_E01_040_Q15##)'
The correct Answer is:6
Topper's Solved these Questions
Similar Questions
A wire of length l, mass m and resitance R slides without any friction down the parallel conducting rails of negligible resistance (Fig). The rails are connected to the wire so that the wire and the rails form a closed rectangular conducting loop. The plane of the rails makes an angle θ with the horizontal and a uniform vertical magnetic field of induction B exists throughout the region. Find the steady-state velocity of the wire
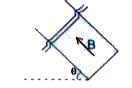
View SolutionA wire of length l, mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle θ with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
View Solution
Knowledge Check
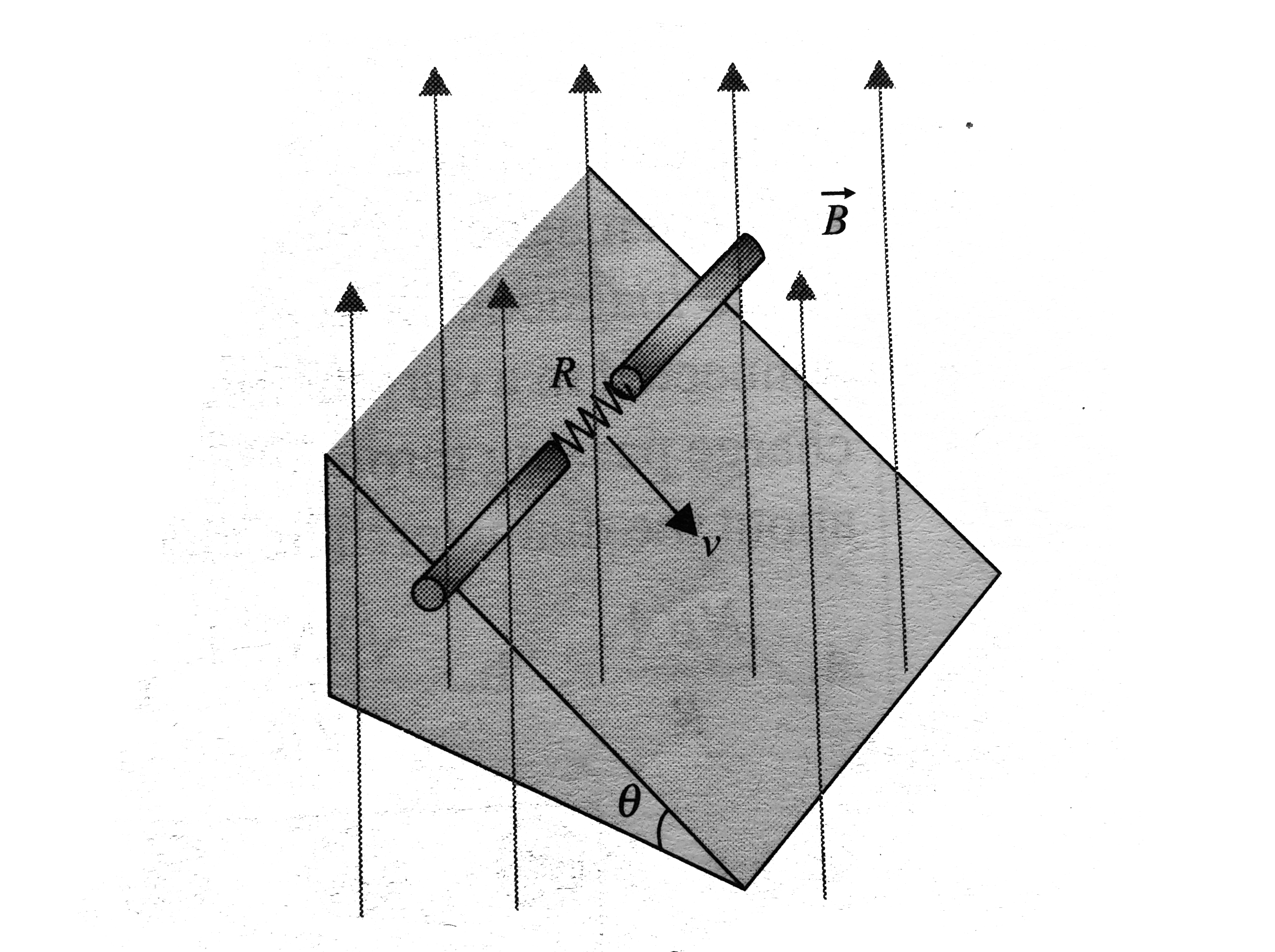
A wire of length l, mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle θ with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
 A(a) mgRsinθB2l2cos2θB(b) mgRsin2θB2l2cos2θC( c) mgRsinθB2l2cos2θD( d) mgRsin2θB2l2cosθ
A(a) mgRsinθB2l2cos2θB(b) mgRsin2θB2l2cos2θC( c) mgRsinθB2l2cos2θD( d) mgRsin2θB2l2cosθA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
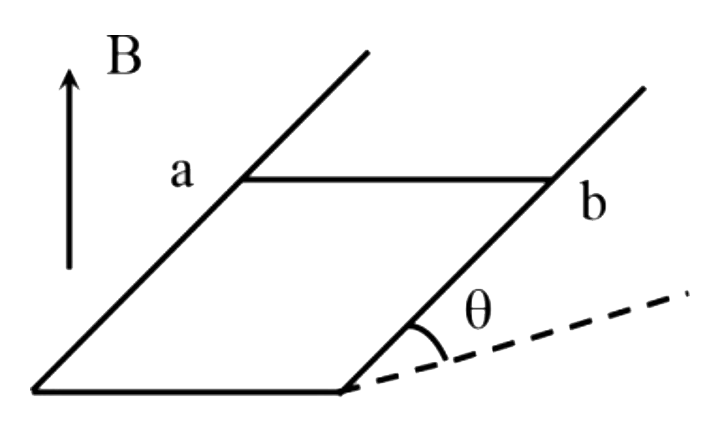 A√mgRvl2cos2θB√mgRcosθvl2sin2θC√mgRv2l2sin2θD√mgRsinθvl2cos2θ
A√mgRvl2cos2θB√mgRcosθvl2sin2θC√mgRv2l2sin2θD√mgRsinθvl2cos2θA wire cd of length l and mass m is sliding without friction on conducting rails ax and by as shown. The verticle rails are connected to each other with a resistance R between a and b. A uniform magnetic field B is applied perpendicular to the plane abcd such that cd moves with a constant velocity of
 AmgRBlBmgRB2l2CmgRB3l3DmgRB2l)
AmgRBlBmgRB2l2CmgRB3l3DmgRB2l)
A wire ab of length l, mass m and resistance R slided on a smooth, thick pair of metallic rails joined at the bottom as shown in . The plane of the the rails makes an angle θ with the horizontal. A vertical magnetic field B exists in the ragion. if the wire slides on the rails at a constant speed v, show that B=√mgRsinθvl2cosθ.
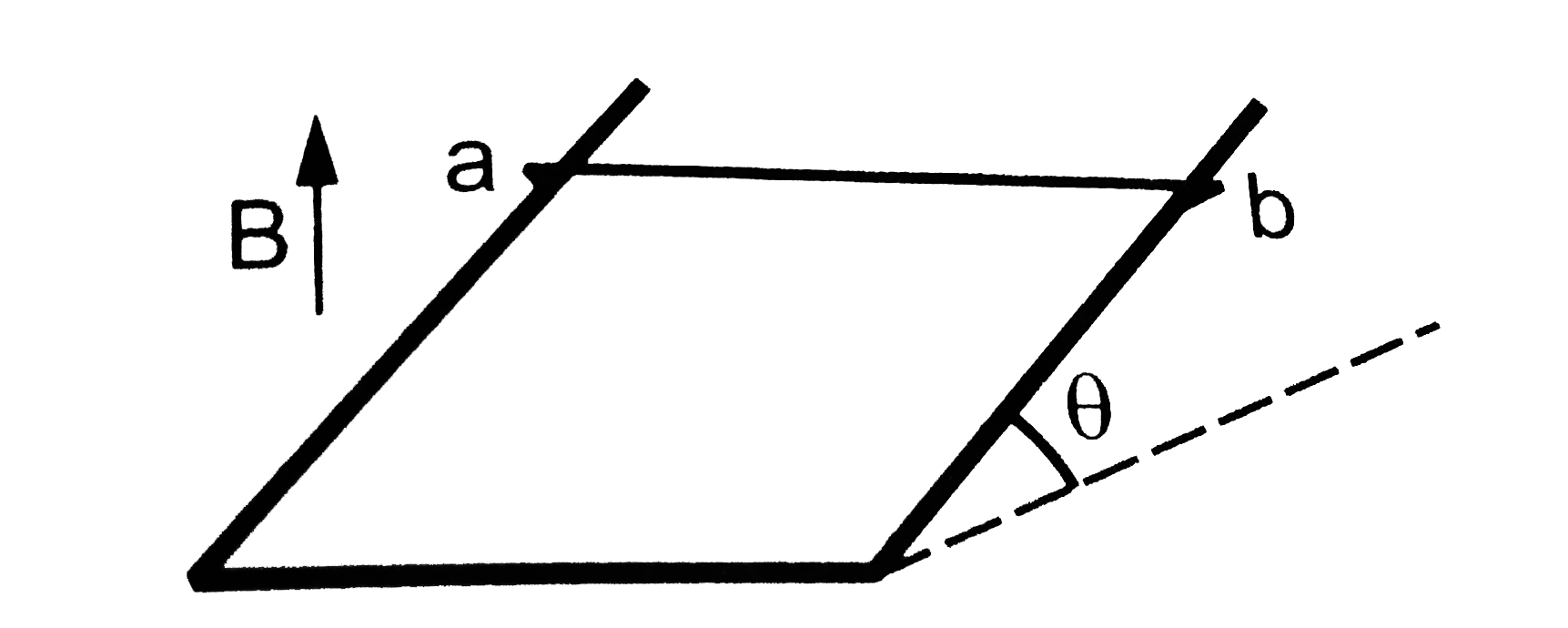
View SolutionA conducting wire ab of length l, resistance r and mass m starts sliding down a smooth vertical, thick pair of perfectly conducting rails as shown in the figure. A uniform magnetic field B exist in the space in the figure. A uniform magnetic field B exist in the space in a direction perpendicular to the plane of the rails. What will be the final constant speed of wire?
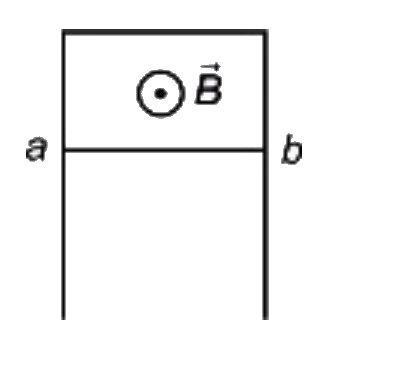
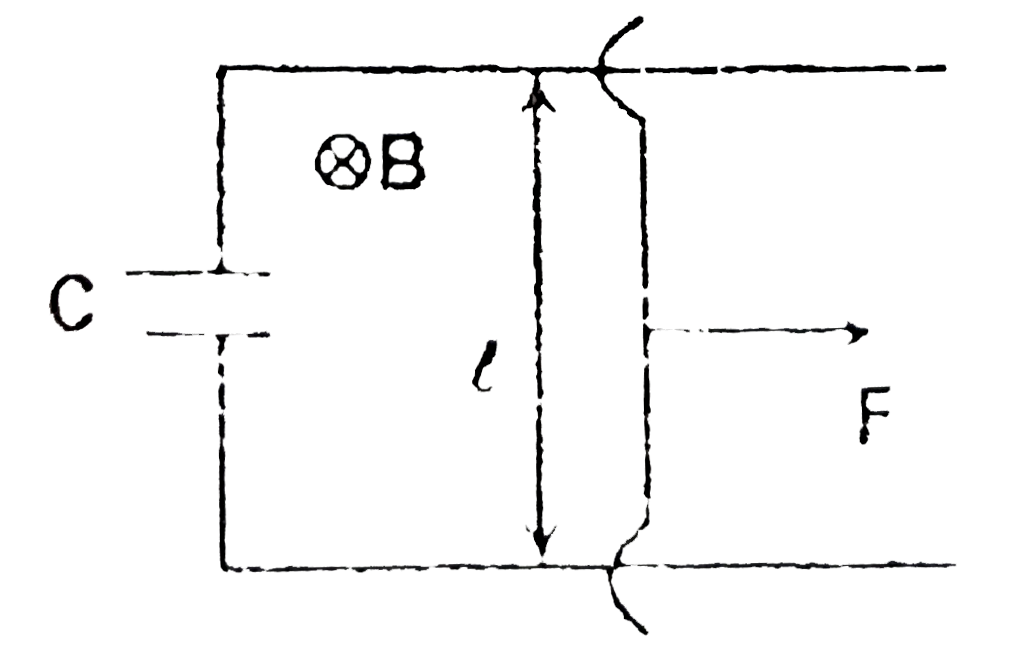
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
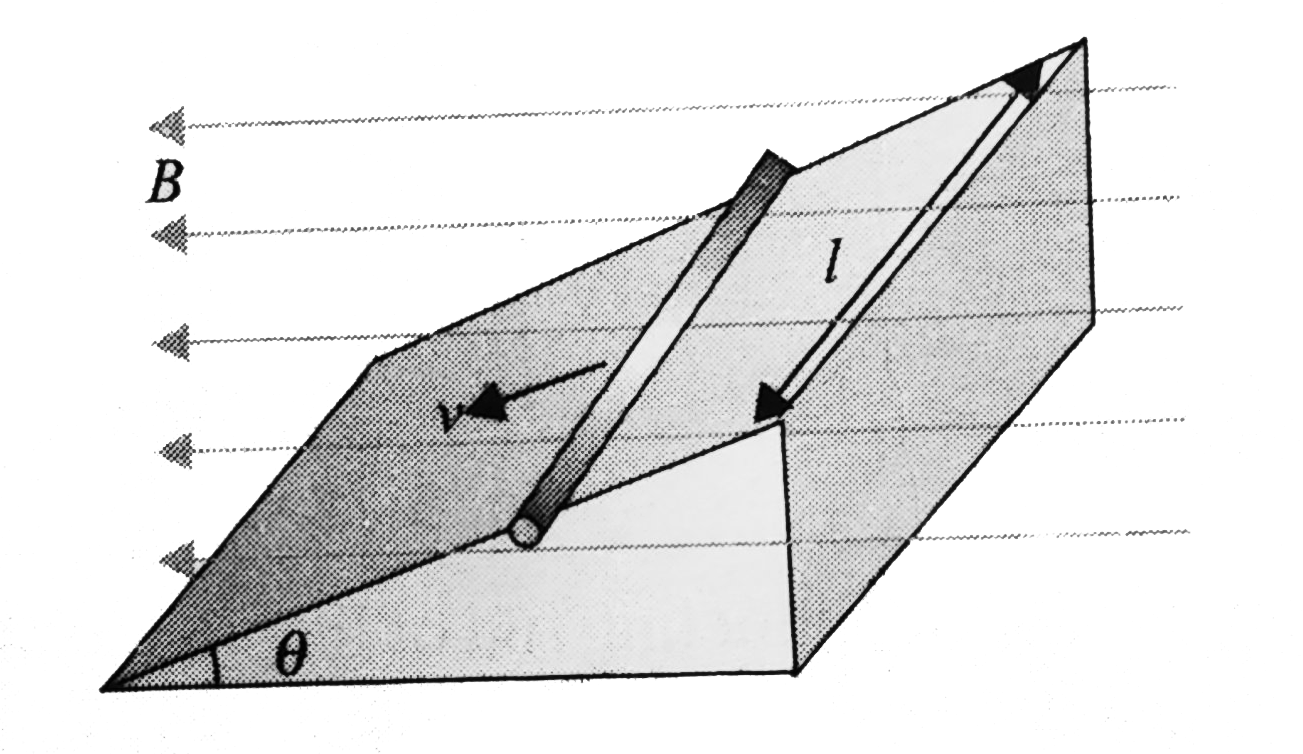
View SolutionA rod of mass m, length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v. If a uniform horizontal magnetic field B exists, then find thevalue of B.
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then

View Solution
