The motion of a particle along x-axis is given by equation x = 9+5t2 , where x is the distance in cm and t is time in second. Find
average velocity during the interval from 3 to 5 secondsSolution in Assamese
Step by step video & image solution for The motion of a particle along x-axis is given by equation x = 9+5t^2 , where x is the distance in cm and t is time in second. Find average velocity during the interval from 3 to 5 seconds by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Distinguish between distance and displacement
View SolutionWhat is the basic different between a vector and a scalar?
View SolutionA particle is moving along the x-axis such that s=6t-t^(2) , where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5 s .
View SolutionX -अक्ष पर गतिमान एक कण का स्थिति समय (x−t) ग्राफ चित्र में प्रदर्शित है। ज्ञात कीजिए-
(i) t=0 सेकण्ड से t=2सेकण्ड तक के समयन्तराल में कण का विस्थापन, तय दूरी, औसत चाल, औसत वेग।
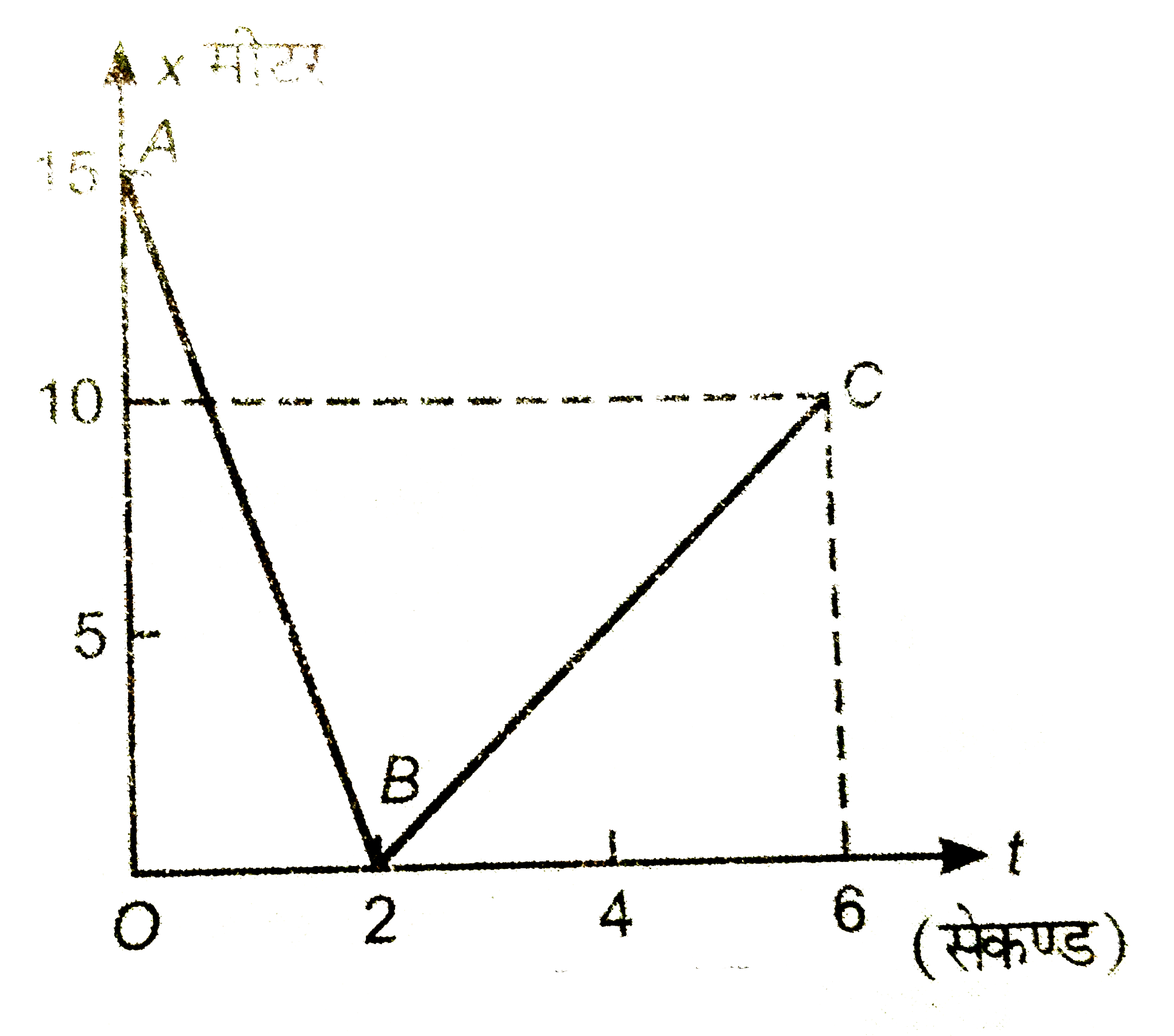
(i) t=0 सेकण्ड से t=6 सेकण्ड तक के समयान्तराल में कण का विस्थापन, तय दूरी, औसत चाल एवं औसत वेग।
(iii) t=1 सेकण्ड तथा t=3 सेकण्ड पर कण का वेग।
View SolutionA particle moves along the x-axis such that its co-ordinate (x) varies with time (t), according to the expression x=2−5t+6t2, where x is in metres and t is in seconds. The initial velocity of the particle is :–
View Solutionएक पिंड एकविमीय गति के कण की स्थिति x (मीटर में) समय t (सेकण्ड में) पर निम्न प्रकार निर्भर करती है -
x=t2−4t+3
ज्ञात कीजिये (i ) समय अंतराल t = 0 से t = 4 सेकण्ड में पिंड का विस्थापन, (ii ) समय अंतराल t = 2 सेकण्ड से t = 4 सेकण्ड के लिये पिंड का औसत वेग |
View Solutionएकविमीय गति में कण स्थिति
x=(3+5t−t2) मीटर है
इस गति के लिये समय अंतराल t = 0 सेकण्ड से t = 4 सेकण्ड तक विस्थापन वेग आरेख खींचिये |
View SolutionThe position x of a particle moving along x - axis at time (t) is given by the equation t=sqrtx+2 , where x is in metres and t in seconds. Find the work done by the force in first four seconds
View SolutionA particle is moving along the x-axis. At any given moment the particle is the equation of position x=a+bt^2 , Where a = 6m and b=3.5 m/s^2 Find the average velocity between t = 3 seconds and t = 6 seconds by expressing t as a unit of seconds
View SolutionEquation of SHM of a particle is x=5cos(π2t) ,where x is in cm and t is in second Then average speed of particle in first five second of motion will be?
View SolutionThe equation of motion of a particle is given by x=5+3sin(πt), where x is in cm and t in seconds. Find the amplitude of motion at one fourth of the time period of motion (in cm):
View SolutionA body moves along x-axis such that its displacement varies with time as given, x=7 + 3t + 5t^2 . The average velocity during 3rd second is
View SolutionThe x -coordinate of a particle moving along x -axis varies with time as x=6-4t+t^(2), where x in meter and t in second then distance covered by the particle in first 3 seconds is
View SolutionThe motion of a particle along x-axis is given by equation x = 9+5t2 , where x is the distance in cm and t is time in second. Find
the displacement after 3 seconds.
View SolutionThe motion of a particle along x-axis is given by equation x = 9+5t2 , where x is the distance in cm and t is time in second. Find instantaneous velocity after 3 seconds
View Solution
