कथन-I : (a+b+c+d)14 प्रसार में ab8c3d2 का गुणांक 180180 होगा|
क्योकि
कथन-II (a1+a2+a3+.....+am)n के प्रसार में व्यापक पद =∑n!n1!n2!n3!....nm!an11an22...anmm जहाँ n1+n2+n3+......+nm=n है
कथन I सत्य है, कथन II सत्य है कथन II, कथन-1 का सही स्पष्टीकरण है।
कथन I सत्य है, कथन सत्य है कथन II, कथन-1 का सही स्पष्टीकरण नहीं है।
कथन-I सत्य है परन्तु कथन-II असत्य है।
कथन -Iअसत्य है परन्तु कथन -II सत्य है।
The correct Answer is:C
Step by step video, text & image solution for कथन-I : (a+b+c+d)^(14) प्रसार में ab^(8)c^(3)d^(2) का गुणांक 180180 होगा| क्योकि कथन-II (a_(1)+a_(2)+a_(3)+.....+a_(m))^(n) के प्रसार में व्यापक पद =sum (n!)/(n_(1) !n_(2) ! n_(3) !....n_(m)!) a_(1)^(n1) a_(2)^(n2) ...a_(m)^(nm) जहाँ n_(1)+n_(2)+n_(3)+......+n_(m)=n है by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -034videos
द्विपद प्रमेय
- BOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -04 [A]28videos
द्विपद प्रमेय
- BOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -03 (स्तम्भ सुमेलन )1videos
द्विपद प्रमेय
- BOOK - ALLEN HINDICHAPTER - द्विघात समीकरण EXERCISE - EXERCISE-4 B11videos
द्विघात समीकरण
- BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-04 [B] (BRAIN STORMING SUBJECTIVE EXERCISE)14videos
बिन्द् एवं सरल रेखा
Similar Questions
यदि n धनात्मक पूर्णांक तथा (1+4x+4x2)n=2n∑r=0arxr जहाँ ai,r,(i=0,1,2,3,...,2n) वास्तविक संख्याये है
2n∑r=0a2r का मान होगा-06:25View Solutionयदि (1+x)18 के विस्तार में (2r+4) वों पद तथा (r−2) वों पद के गुणांक समान हैं, तो r का मान है
14:04View Solution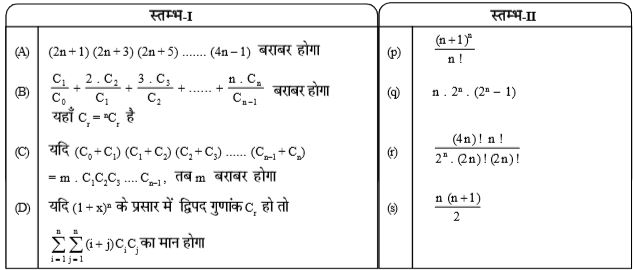
02:54View Solutionयदि द्विघात समीकरण ax2+bx+c=0 का एक मूल दूसरे मूल का n वीं घात के बराबर है, तो दिखाइए की
(acn)1n+1+(anc)1n+1+b=003:48View Solution(-2,-7) से गुजरने वाली तथा सरल रेखाओं 4x + 3y = 12 एवं 4x +3y=3 के मध्य 3 इकाई का अन्तः खण्ड काटने वाली रेखाओं की समीकरण ज्ञात कीजिए।
01:36View SolutionIf a1,a2,a3,,a2n+1 are in A.P., then a2n+1−a1a2n+1+a1+a2n−a2a2n+a2++an+2−anan+2+an is equal to n(n+1)2×a2−a1an+1 b. n(n+1)2 c. (n+1)(a2−a1) d. none of these
04:21View SolutionIf A_(i)=(x-a_(i))/(|x-a_(i)|),i=1,2,3,....n and a_(1)
02:17View SolutionIf a_(1),a_(2)...a_(n) are the first n terms of an Ap with a_(1)=0 and d!=0 then (a_(3)-a_(2))/(a_(2))+(a_(4)-a_(2))/(a_(3))+(a_(5)-a_(2))/(a_(4))...+(a_(n)-a_(2))/(a_(n-1)) is
06:56View SolutionIf A1,A2,.....An are independent events associated with a random experiment; then P(A1∩A2∩.......∩An)=P(A1)P(A2).......P(An)
06:29View SolutionStatement-1: 13+33+53+73+...+(2n−1)3<n4,n∈N
Statement-2: If a1,a2,a3,…,an are n distinct positive real numbers and m>1, then
am1+am2+...+amnn>(a1+a2+...+abn)m05:25View Solutiona1,a2,a3.....an are in H.P. a1a2+a3+...+an,a2a1+a3+...+an,a3a1+a2+a4+...+an,...,ana1+a2+...+an−1 are in
05:51View SolutionProve that am1+am2+….+amnn<(a1+a2+..+ann)m If 0<m<1andai>0 for all I.
06:36View SolutionIf a1,a2,a3,a4,,……,an−1,an are distinct non-zero real numbers such that (a21+a22+a23+…..+a2n−1)x2+2(a1a2+a2a3+a3a4+……+an−1an)x+(a22+a23+a24+......+a2n)≤0 then a1,a2,a3,.....,an−1,an are in
01:56View SolutionSTATEMENT-1 : If a, b, c are in A.P. , b, c, a are in G.P. then c, a, b are in H.P.
STATEMENT-2 : If a1,a2a3……..a100 are in A.P. and a3+a98=50 thena1+a2+a3+….+a100=2500
STATEMENT-3 : If a1,a2,.......,an≠0 then a1+a2+a3+.......+ann≥(a1a2.........an)1/n05:09View SolutionIf a_(1),a_(2) , a_(3),"……..",a_(n) are in H.P. , then : (a_(1))/( a_(2) + a_(3) +"........."+a_(n)),(a_(2))/(a_(1) + a_(3)+"..........."+a_(n)),"......",(a_(n))/(a_(1)+a_(2)+"........"a_(n-1)) are in :
01:31View Solution