Show that the area of the triangle contained between the vectors →Aand→B is one-half the magnitude of →A×→B.
F=ma⇒a=Fm=205=4m/s2
v=0 (initial point) =>v=u+at
⇒v=0+4×10=40m/s.
KE=12mv2=12×5×(40)2=4000Joule
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-2 EXERCISE - SECTION-C9videos
SAMPLE QUESTION PAPER-2
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-2 EXERCISE - SECTION-D10videos
SAMPLE QUESTION PAPER-2
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-2 EXERCISE - SECTION-D10videos
SAMPLE QUESTION PAPER-2
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 5EXERCISE - SECTION - D (Answer all questions.)6videos
SAMPLE QUESTION PAPER 5
- BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER-3 EXERCISE - SECTION-D6videos
SAMPLE QUESTION PAPER-3
Similar Questions
Knowledge Check
- Question 1 - Select One
If the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
ABA2cosθBBA2sinθCBA2sinθcosθDzero - Question 2 - Select One
The angle between the two vectors →a+→b and →a−→b is
ABetween 0∘ and 180∘B90∘ onlyC0∘ onlyD180∘ only - Question 3 - Select One
The angle between →a×→band→b×→a is
AZeroBπCπ/2Dπ/4
Let →a,→band→c be unit vector such that →a+→b−→c=0. If the area of triangle formed by vectors →aand→b is A, then what is the value of 4A2 ?
View SolutionFind the angle between two vectors →aand→b with magnitudes 1 and 2 respectively and satisfying →a.→b.=1
View SolutionIf the area of a triangle of sides →A&→B is equal to AB4, then find the acute angle between →A&→B.
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
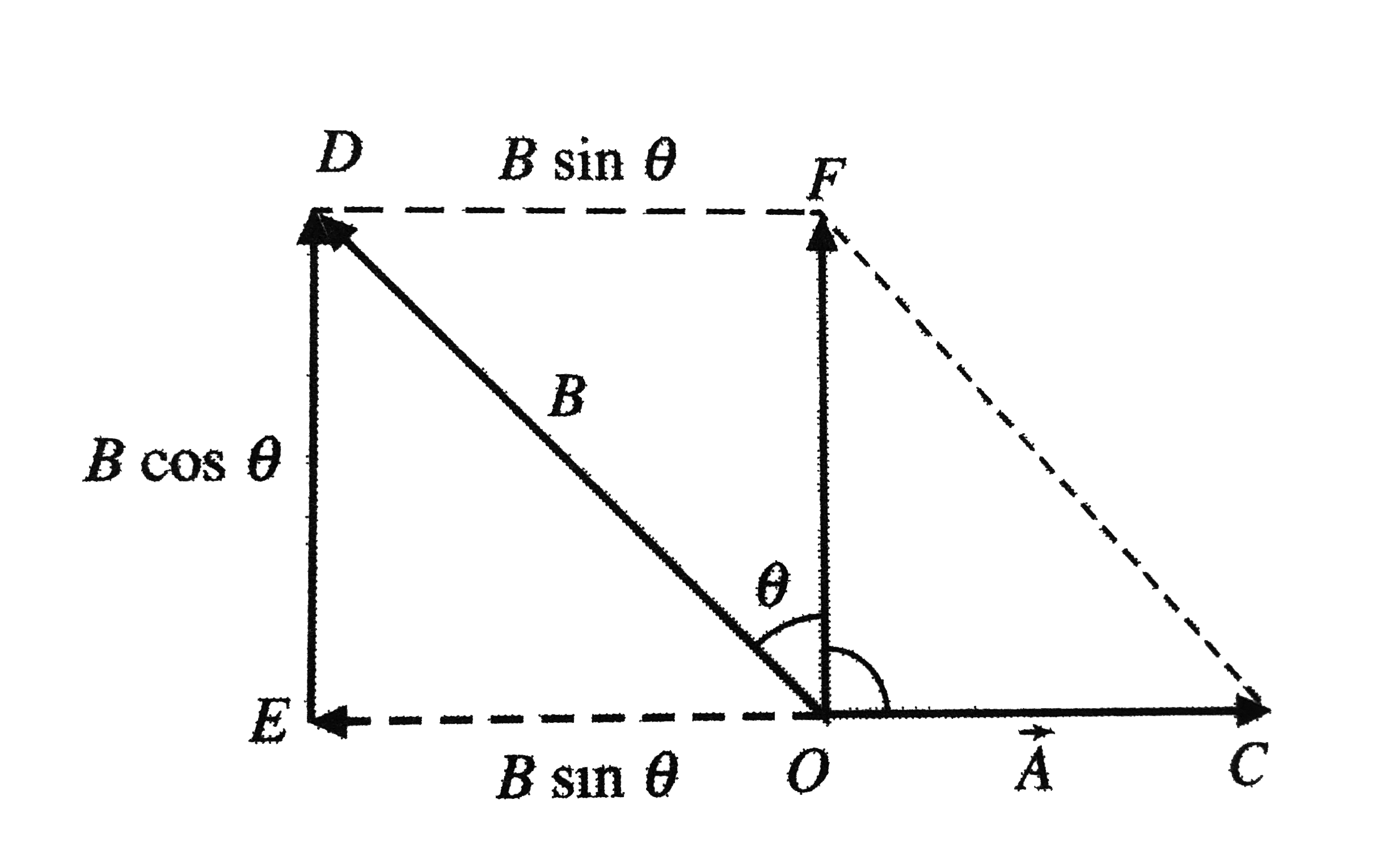 .View Solution
.View SolutionIf the angle between the vectors →aand→b is π3 and the area of the triangle with adjacemnt sides parallel to →aand→b is 3 , then a.b is
View Solution

