A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
If t = 0 when T is 72, then the value of c is
−2
0
2
Log 2
The correct Answer is:D
Step by step video, text & image solution for A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6^(@)F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4^(@)F. The room in which the cat was put is always at 70^(@)F. The normal temperature of the cat is taken as 98.6^(@)F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: (dT)/(dt) prop (T − 70), where 70^(@)F is the room temperature and T is the temperature of the object at time t. Substituting the two different observations of T and t made, in the solution of the differential equation (dT)/(dt)=k(T-70) where k is a constant of proportion, time of death is calculated. If t = 0 when T is 72, then the value of c is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - CBSE MODEL PAPERCHAPTER - QUESTION BANK 2021EXERCISE - QUESTIONS9videos
QUESTION BANK 2021
- BOOK - CBSE MODEL PAPERCHAPTER - Additional Practice QuestionsEXERCISE - Question47videos
Additional Practice Questions
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE QUESTION PAPER ( MATHEMATICS )EXERCISE - QUESTION60videos
SAMPLE QUESTION PAPER ( MATHEMATICS )
Similar Questions
A Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
State the degree of the above given differential equation.04:58View SolutionShown below is the graph of a function f(x) whose domain is R – (-1,1). Some portion of the graph is hidden behind the star.
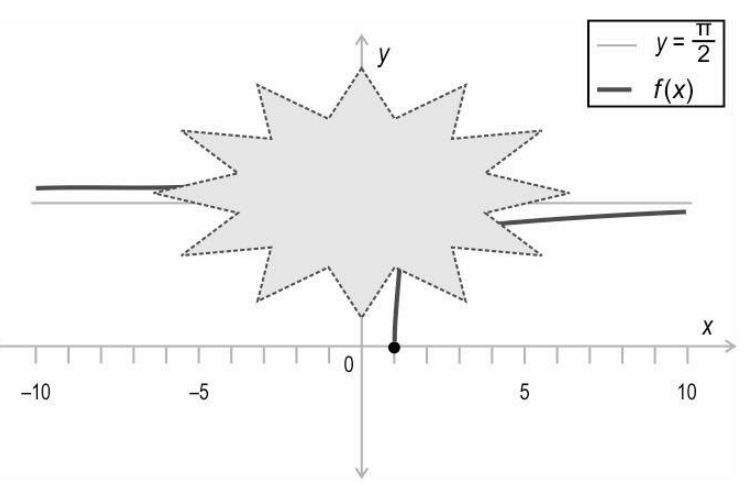
Which of the following is f(x)?01:38View SolutionCheck whether the function F:R→ R defined asF(X)=x2is one-one or not.
View SolutionThe doctor took the temperature of a dead body at 11.30 Pm which was 94.6∘F. He took the temperature of the body again after one hour, which was 93.4∘F. If the temperature of the room was 70∘F , estimate the time of death. Taking normal temperature of human body as 98.6∘F. [Given: log(143123)=0.15066,log(123117)=0.05 ]
08:38View Solutionनिम्नलिखित में से कौन-सी आकृति कुत्ता, बिल्ली और पालतू पशु का संबंध दर्शाती है?
01:42View SolutionThe magician took pity on the mouse. He turned it into a cat.
01:50View SolutionThe doctor took the temperature of a dead body at 11.30 Pm which was 94.6∘F. He took the temperature of the body again after one hour, which was 93.4∘F. If the temperature of the room was 70∘F , estimate the time of death. Taking normal temperature of human body as 98.6∘F. [Given: log(143123)=0.15066,log(123117)=0.05 ]
07:22View SolutionA Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
State the degree of the above given differential equation.03:58View SolutionA Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
Which method of solving a differential equation helped in calculation of the time of death?02:38View SolutionA Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
If the temperature was measured 2 hours after 11.30pm, will the time of death change? (Yes/No)View SolutionA Veterinary doctor was examining a sick cat brought by a pet lover. When it was brought to the hospital, it was already dead. The pet lover wanted to find its time of death. He took the temperature of the cat at 11.30 pm which was 94.6∘F. He took the temperature again after one hour, the temperature was lower than the first observation. It was 93.4∘F. The room in which the cat was put is always at 70∘F. The normal temperature of the cat is taken as 98.6∘F when it was alive. The doctor estimated the time of death using Newton law of cooling which is governed by the differential equation: dTdt∝(T−70), where 70∘F is the room temperature and T is the temperature of the object at time t.
Substituting the two different observations of T and t made, in the solution of the differential equation dTdt=k(T-70) where k is a constant of proportion, time of death is calculated.
The solution of the differential equation dTdt=k(T−70) is given by,01:36View SolutionIn an experiment, a student took pure liquid and started boiling. He noted the boiling temperature of that liquid. After he took sand solution and started boiling and he noted the temperature. Based on the above experiment, what is his observation?
View SolutionHe took the man ............. hospital.
01:05View SolutionWhen kala woke up, her body temperature was 102°F. She took medicine for fever. After 2 hours it was 2°F lower, What was her temperature then?
View SolutionWhen Kala woke up, her body temperature was 102^(@)° . She took medicine for fever. After 2 hours it was 2^(@) lower. What was her temperature then?
01:42View Solution

