Mr. Kumar borrowed Rs 15,000for two years. The rate of interest for the two successive years are 8% and 10% respectively. If he repays Rs 6,200 at the end of the first year, find the outstanding amount at the end of the second year.
To solve the problem step by step, we will calculate the simple interest for each year, adjust for the repayment made at the end of the first year, and finally determine the outstanding amount at the end of the second year.
Step 1: Calculate the Simple Interest for the First Year
The formula for Simple Interest (SI) is given by:
SI=P×R×T100
Where:
- P = Principal amount (initial loan) = Rs 15,000
- R = Rate of interest for the first year = 8%
- T = Time in years = 1
Substituting the values:
SI=15000×8×1100=120000100=1200
Step 2: Calculate the Amount at the End of the First Year
The total amount at the end of the first year is the sum of the principal and the simple interest calculated:
Amount=P+SI=15000+1200=16200
Step 3: Adjust for the Repayment Made at the End of the First Year
Mr. Kumar repays Rs 6,200 at the end of the first year. We need to find the outstanding principal after this repayment:
Outstanding Principal=Amount−Repayment=16200−6200=10000
Step 4: Calculate the Simple Interest for the Second Year
Now, we will calculate the simple interest for the second year using the outstanding principal:
- New Principal P = Rs 10,000 (outstanding amount after repayment)
- Rate of interest R = 10%
- Time T = 1 year
Using the SI formula again:
SI=10000×10×1100=100000100=1000
Step 5: Calculate the Amount at the End of the Second Year
The total amount at the end of the second year is:
Amount=P+SI=10000+1000=11000
Final Answer
The outstanding amount at the end of the second year is Rs 11,000.
---
The formula for Simple Interest (SI) is given by:
SI=P×R×T100
Where:
- P = Principal amount (initial loan) = Rs 15,000
- R = Rate of interest for the first year = 8%
- T = Time in years = 1
SI=15000×8×1100=120000100=1200
The total amount at the end of the first year is the sum of the principal and the simple interest calculated:
Amount=P+SI=15000+1200=16200
Mr. Kumar repays Rs 6,200 at the end of the first year. We need to find the outstanding principal after this repayment:
Outstanding Principal=Amount−Repayment=16200−6200=10000
Now, we will calculate the simple interest for the second year using the outstanding principal:
- New Principal P = Rs 10,000 (outstanding amount after repayment)
- Rate of interest R = 10%
- Time T = 1 year
SI=10000×10×1100=100000100=1000
The total amount at the end of the second year is:
Amount=P+SI=10000+1000=11000
The outstanding amount at the end of the second year is Rs 11,000.
Topper's Solved these Questions
Similar Questions
A manufacturer sells a washing machine to a wholsaler for Rs 15,000. The wholsaler sells it to a trader at a profit of Rs 1,200 and the trader in turn sells it to a consumer at a profit of Rs 1,800. If the rate of VAT is 8% find,
(i) The amount of VAT received by the State Government on the sale of this machine from the manufacturer and the wholsaler.
(ii) The amount that the consumer pays for the machine.
View SolutionUse a graph paper for this question take 1 cm = 1 unit along both the X and Y axis :
(i) Plot the points A(0, 5), B(2, 5), C(5, 2), D(5, -2), E(2, -5) and F(0, -5).
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
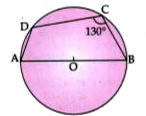
∠BCD=130∘. Find
(i) ∠DAB
View SolutionA man who borrowed a certain sum agrees to repay it by paying Rs. 4032 at the end of the first year and Rs. 10075 at the end of the second year. If the rate of simple interest is 12% per annum, find the sum borrowed.
View SolutionJahangir borrowed Rs 80,000 at the rate of 7% per annum at compound interest, interest being compounded annually. How much should he repay at the end of the first year, so that by repaying Rs 48,792 at the end of the first year, so that by repaying Rs 48,792 at the end of second year, then what is the rate of interest?
View SolutionAmit borrowed ₹ 800 at 10% rate of interest. He repaid ₹ 400 at the end of first year. What is the amount required to pay at the end of second year to discharge his loan which- was calculated at compound interest?
View Solution1875 रु. पर 2 वर्ष में चक्रवृद्धि ब्याज की राशि कितनी होगी. यदि पहले वर्ष ब्याज की दर 4% है और दूसरे वर्ष 8% है?
View SolutionCalculate the amount and the compound interest on Rs. 5,000 in 2 years, if the rates of interest for the successive years be 8% and 10% respectively.
View SolutionPeter borrows Rs. 12,000 for 2 years at 10% p.a. compound interest. He repays Rs. 8,000 at the end of first year. Find :
the amount at the end of first year, after making the repayment.
View SolutionPeter borrows Rs. 12,000 for 2 years at 10% p.a. compound interest. He repays Rs. 8,000 at the end of first year. Find :
the amount at the end of first year, after making the repayment.
View SolutionPeter borrows Rs. 12,000 for 2 years at 10% p.a. compound interest. He repays Rs. 8,000 at the end of first year. Find :
the principal for the second year.
View SolutionPeter borrows Rs. 12,000 for 2 years at 10% p.a. compound interest. He repays Rs. 8,000 at the end of first year. Find :
the amount to be paid at the end of second year, to clear the debt.
View SolutionFind the amount and the compound interest on Rs. 4,000 in 2 years, if the rate of interest for first year is 10% and for the second year is 15%.
View SolutionA man borrowed a sum of money and agrees to pay it off by paying Rs 43,200 at the end of the first year and Rs 34,992 at the end of the second year. If the rate of compound interest is 8% per annum, find the sum borrowed.
View SolutionWhat principal will amount to Rs 9,856 in two years, if the rates of interest for successive years are 10% and 12% respectively ?
View Solution
