The three boxes in this diagram represent the three major biosynthetic pathways in aerobic respiration. Arrows represent net reactants or products.
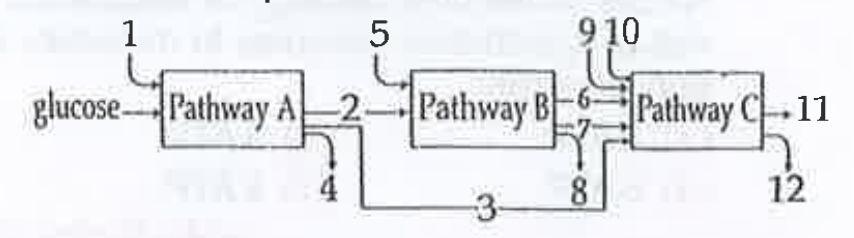
Arrows numbered 4, 8 and 12 can all be
ATP
H2O
FAD+ or FADH2
NADH
The correct Answer is:A
Step by step video & image solution for The three boxes in this diagram represent the three major biosynthetic pathways in aerobic respiration. Arrows represent net reactants or products. Arrows numbered 4, 8 and 12 can all be by Biology experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RESPIRATION IN PLANTS EXERCISE - Assignment (Section D)10videos
RESPIRATION IN PLANTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RESPIRATION IN PLANTS EXERCISE - Assignment (Section B)35videos
RESPIRATION IN PLANTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - REPRODUCTIVE HEALTH EXERCISE - Sectoin -D Assertion - Reason Type Questions22videos
REPRODUCTIVE HEALTH
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEXUAL REPRODUCTION IN FLOWERING PLANTS EXERCISE - Assignment (SECTION D)20videos
SEXUAL REPRODUCTION IN FLOWERING PLANTS
Similar Questions
Which intermediate product is found in all three of the following process
(a) anaerobic respiration
(b) aerobic respiration
(c) photosynthesisView SolutionIn a hexagonal system system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-packed is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed overt the first layer so that they touch each other and represent the second layer so that they touch each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is converted with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
(a)4
(b)6
(c)12
(d)17View Solution
Knowledge Check
- Question 1 - Select One
The chart below shows the number of small and large packages of a certain brand of cereal that were bought over a three - day period. The proce of a small box of this brand is $ 2.99, and the price of a large box is $3.99. Which of the following matrix expression represents the income, in dollars, received from the sale of cereal each of the three days ?
Day 1Day 2Day 3Large758257Small433650A[758257433650][2.99 3.99]B⎡⎢⎣754382365750⎤⎥⎦[3.992.99]C[758257433650][2.993.99]D[2.993.99]⎡⎢⎣754382365750⎤⎥⎦ - Question 2 - Select One
To make its sales goals for the month, a toy manufacture must sell at least $10,400 for of toy hoops and basketballs. Toy hoops sell for $8 and basketballs sell for $25. The company hopes to sell more than three times as many basketballs as toy hoops. If h represents the number of toy hoops and b represents the number of basketballs, where h and b are positive integer, which of the following systemsof inequalities best describes this situation ?
A8h+25b≥10
400b>3hB8h+25b≥10
400>3bC25h+8b≥10
400b>3hD25h+8b≥10
400h>3b - Question 3 - Select One
Time Travel has long intrigued us, it's enough to spur a whole sub-genre of science fiction. It's mind-boggling to consider all of the implication of traveling through time and having free will. It's easy to see that the universe as we know it would be rather unstable if, for instance, you could travel backwards in time and kill your own grandfather.But is it possible? To begin to understand the posiblities of time, we first need a brief introduction of spacetime. We're all familiar with our three-dimensional world, but we need to consider a fourth dimension as well-time. Therefore,you can sit still in a chair not travelling in three-dimensions, but traveling in spacetime. we think of times as passing forward. stephen Hawking explains this as three "arrows of time". The thermodynamic arrow of time points from a time of low entropy (high organization) to a time of high entropy (low organization/high choas). It passes from a glass of water sitting on a table to a shattered glass and a pundle of water on the floor. There's a psychological arrow of time: we remember the past, but not the future. Finally, there's a cosmological arrow of time. The universe is expanding (though this arrow could reverse in the future). We tend to think of time as an absolute: there are 60 seconds in every minute, and my 60 seconds should be the same as your 60 seconds. However, Einstein's theory of relativity defies this with time dilation. When a body approaches the speed of light, time efficency slow down. Therefore, if observes traveling at different fractions of the speed of light were to hold clocks, the clocks would be ticking at different speeds. Tie is relatives to the observer, rather than absolute. Consider what's reffered to as the twin paradox: one identical rwin aboard the spaceship will experience time dilation, and thus will age less quickly than the twin at home. Furthermore, if the twin's journey were long enough, the twin could return to earth to find that everyone he or she once knew was long dead. Essentially, this would be travelling into the future. This isn't the exciting kind of time travel from the sci-fi books and movies, though. We would prefer our time travel to be instanteous and not limited to the future. So far, we've examined only linear time travel in the form of slowing time down. But does time have to paas linearly? Is it possible that there could be loops in spacetime leading to the past and future? ONe possible candidate for such travel is the presence of wormholes. While wormholes also seem the stuff of sci-fi, their basis is actually in a paper written by Einstein and Nathan Rosen, where they refer to "bridges"in spacetime. They believed bridges to be extremely unstable and thus only temporary. The idea behind these bridges/wormholes is that there are theoretical tunnels between two far apart locations in spacetime. The distance of the wormhole wouldn't necessarily have to correspond to the distance between the two locations. There is evidence that such wormholes could theoreticaly exist, but that is beyond the scope of this paper. We'll suffice it to say that even if we find such wormholes, we'd have to figure out how to stabilize them in order to utilize them for time travel. Stephen Hawking currently believes time travel into the past to be impossible for many reasons. One less than scientific reason is that humans tend to love "spilling the beans." If someone in the future had figured out how to time travel into the past, he or she likely would have traveled back and told us! So will we eventually be able to time travel without limit? I can't say, my psychological arrow of time doesn't point that way. Oh well, it's all relatives anyway.
Q. Which option gives the best evidence for the answer to the previous question?ALines 13-14 ("There's a…future)"BLines 19-21("When a…speeds")CLines 25-27("Furthermore…future")DLines 28-29 ("This isn't…future")
figure depicts a block sliding along a frictionless ramp in vertical plane Eight numbered arrows in the diagram repreesent direction to be referred to when answering the questions
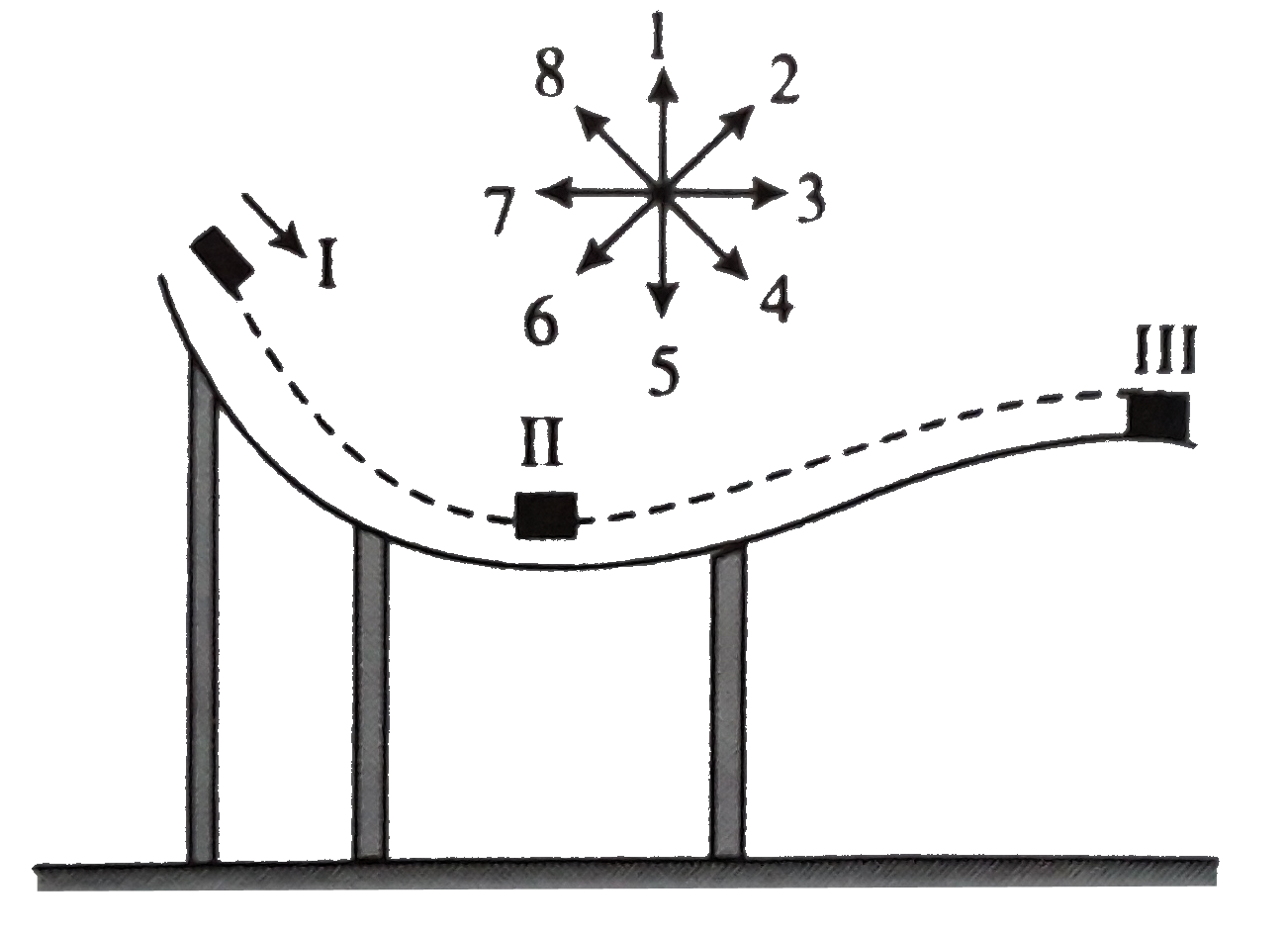
Position - i : Starts sliding on curve path
Position - ii : Lowest position of the curve path
Position - iii : Just outside of the curve path
The direction of the acceleration of the blocks when in position ii is best represented by which of the arrows in the diagram?View Solutionfigure depicts a block sliding along a frictionless ramp in vertical plane Eight numbered arrows in the diagram repreesent direction to be referred to when answering the questions
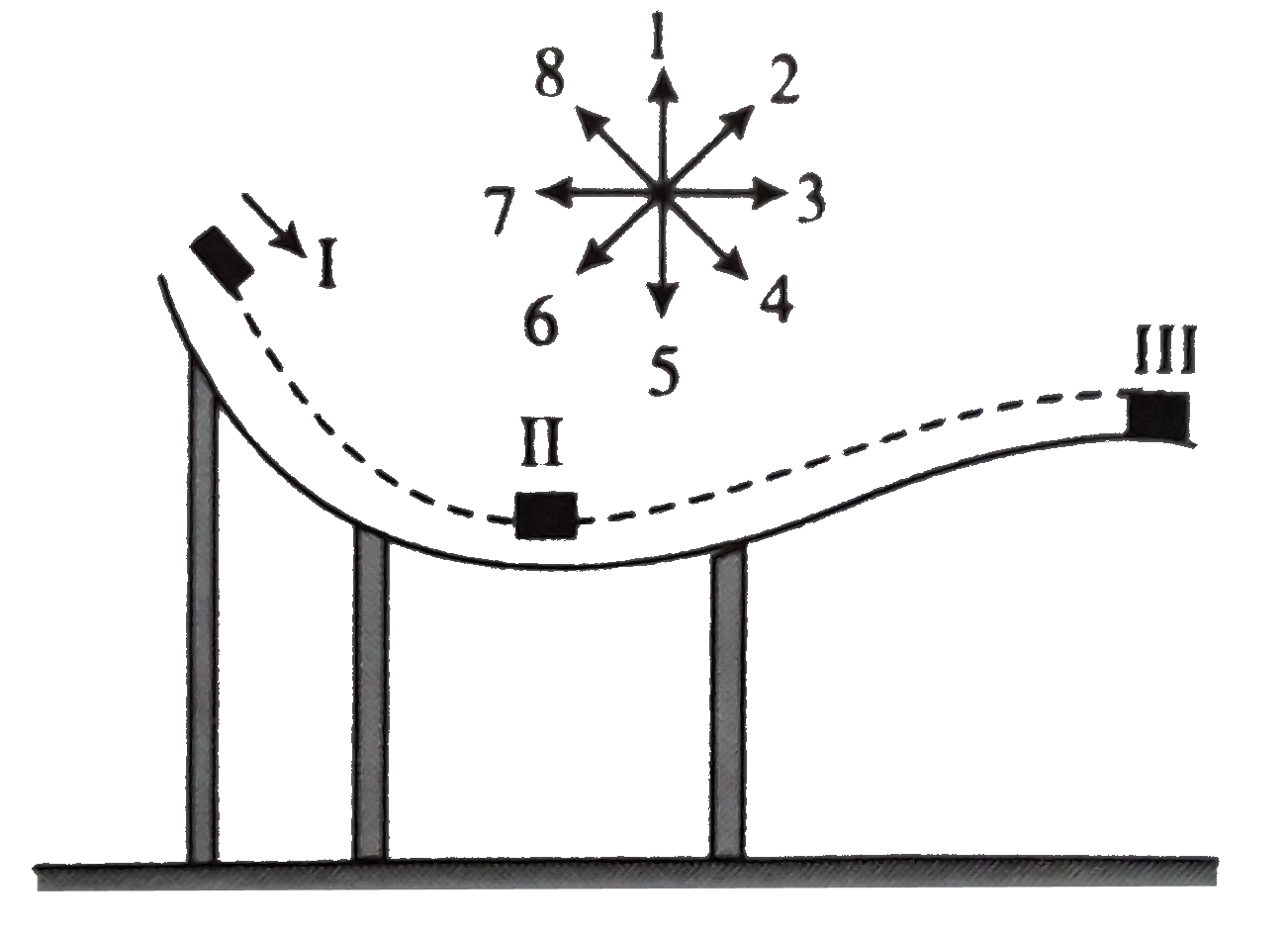
Position - i : Starts sliding on curve path
Position - ii : Lowest position of the curve path
Position - iii : Just outside of the curve path
The direction of the acceleration of the blocks (after leaving the ramp) at position i is best represented by which of the arrows in the diagram?View SolutionPhase space deagrams are useful tools
.
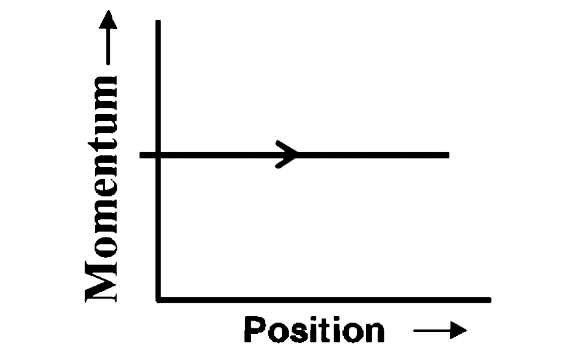in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
The plase space deagram for simple harmonic motion is a circle centered at the origin. In the figure, the two circles represent the same oscillator but for different initial condetions, and E_(1) and E_(2) the total mechanical energies respectivey.
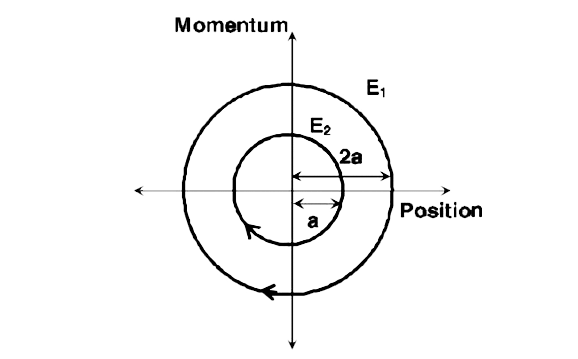.View SolutionPhysical and chemical equilibria can respond to a change in their pressure, temperature, and concentration of reactants and products. To describe the change in the equilibrium, we have a principle named Le Chatelier's principle. This we can define in terms of energy, as the free energy change in equilibrium is zero means the system is stable. So if we are doing some changes in equilibrium, then the system having a tendency to reestablish the equilibrium by undoing the effect we brought. Consider the following equilibrium.
Three sparingly soluble salts A2B,AB, and AB3 are given. If all the three having the same value of solubility products (Ksp), in the saturated solution, the correct order of their solubilites isView Solution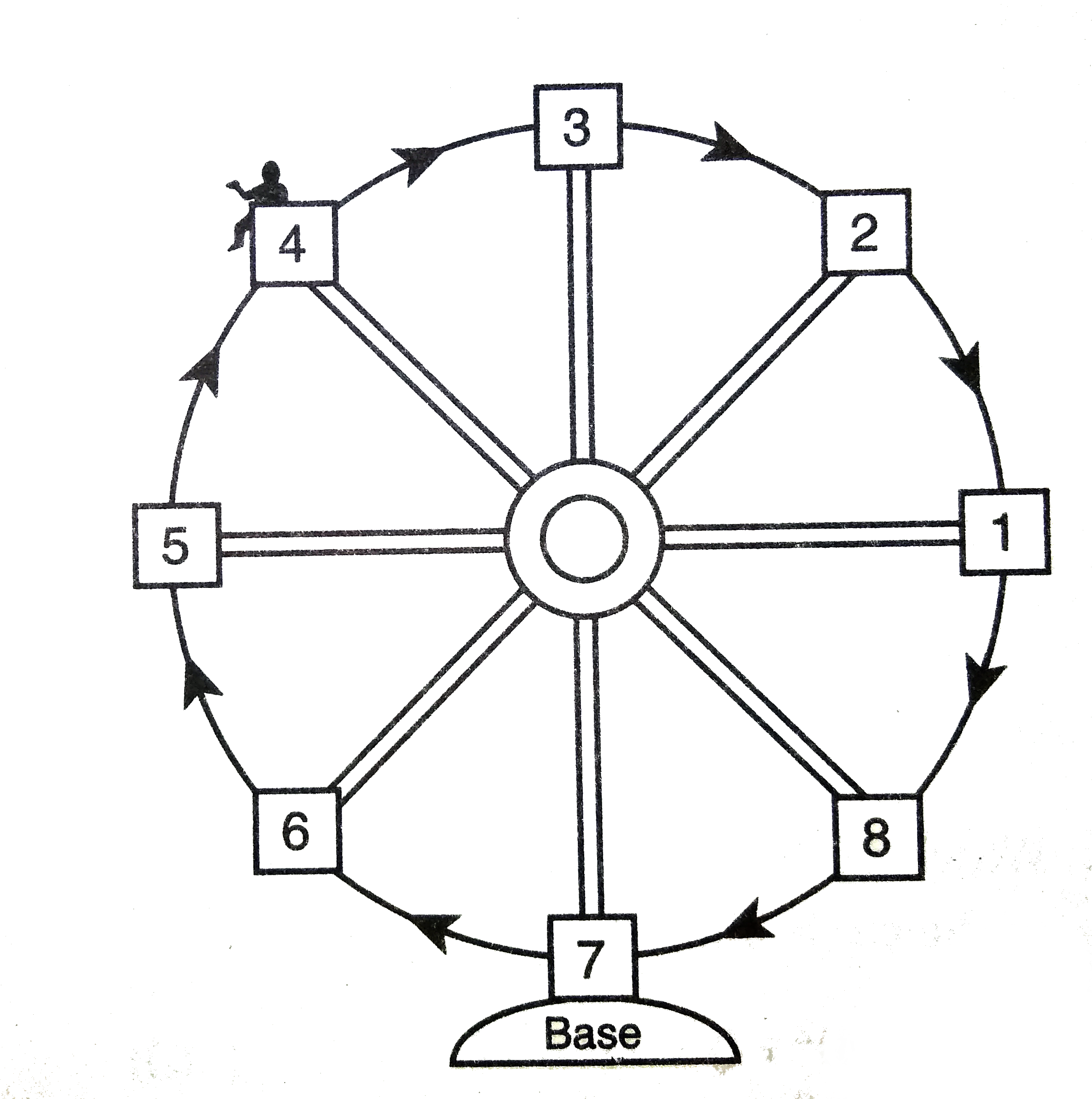
Kristine is riding in car 4 of the ferris wheel represented in the diagram above, which is 84π meters from car 8. The ferris wheel is rotating in the direction indicated by the arrows. If each of the cars are equally spaced around the circular wheel, what is the best estimate of the number of meters in the distance through which kristine's car will travel to reach the botton of the ferris wheel before her car returns to the same position?View Solution