Which defect causes decreases in the density of crystal?
Schottky defect
Frenkel defect
Interstitial defect
Metal excess defect
The correct Answer is:A
Step-by-Step Solution:
1. Understanding Crystal Defects:
- Crystals can have various defects that affect their properties, including density. The main types of defects include Schottky defects, Frenkel defects, interstitial defects, and metal excess defects.
2. Analyzing Each Defect:
- Frenkel Defect: In this defect, a small cation leaves its original position but remains within the crystal structure. Since no particles leave the crystal, the density remains unchanged.
- Interstitial Defect: Here, some particles occupy interstitial sites within the crystal. This addition of particles increases the overall mass without significantly changing the volume, leading to an increase in density.
- Metal Excess Defect: This defect is characterized by anionic vacancies and the presence of extra cations in interstitial sites. The overall mass may not decrease, and hence, the density does not decrease.
- Schottky Defect: In this defect, both cations and anions leave the crystal lattice to maintain electrical neutrality. This loss of particles results in a decrease in the overall mass of the crystal, leading to a decrease in density.
3. Conclusion:
- Among the defects analyzed, the Schottky defect is the one that causes a decrease in the density of the crystal due to the loss of both cations and anions from the lattice.
Final Answer:
The defect that causes a decrease in the density of the crystal is the Schottky defect.
---
- Crystals can have various defects that affect their properties, including density. The main types of defects include Schottky defects, Frenkel defects, interstitial defects, and metal excess defects.
- Frenkel Defect: In this defect, a small cation leaves its original position but remains within the crystal structure. Since no particles leave the crystal, the density remains unchanged.
- Interstitial Defect: Here, some particles occupy interstitial sites within the crystal. This addition of particles increases the overall mass without significantly changing the volume, leading to an increase in density.
- Metal Excess Defect: This defect is characterized by anionic vacancies and the presence of extra cations in interstitial sites. The overall mass may not decrease, and hence, the density does not decrease.
- Schottky Defect: In this defect, both cations and anions leave the crystal lattice to maintain electrical neutrality. This loss of particles results in a decrease in the overall mass of the crystal, leading to a decrease in density.
- Among the defects analyzed, the Schottky defect is the one that causes a decrease in the density of the crystal due to the loss of both cations and anions from the lattice.
The defect that causes a decrease in the density of the crystal is the Schottky defect.
Topper's Solved these Questions
- THE SOLID STATE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - ASSIGNMENT SECTION-C (OBJECTIVE)
17 Videos
- THE SOLID STATE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - ASSIGNMENT SECTION-D (LINKED COMPREHENSION)
9 Videos
- THE SOLID STATE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE SOLID STATE EXERCISE - ASSIGNMENT SECTION-A (OBJECTIVE)
50 Videos
- THE S-BLOCK ELEMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THE S-BLOCK ELEMENTSEXERCISE - Assignment (Section-J)
10 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (Section -D) Assertion-Reason Type Questions
15 Videos
Similar Questions
Why does Schottky defect decrease the desity of a crystal ?
View Solutionwhich of the following statement are not true ?
(a) Vacancy defect results in a decrease in the density of the substance
(b)interstitial defects results in an increase in the density of the substance
(c)impurity defect has no effect on the density of the substance
(d)Frenkel defect results results in an increase in the density of the substance
View SolutionIonic lattic has two major points defects ,(1) Schottky (2) Frenkel defects . Schottkly defects occurs due to the cations - anion pair's missing from the lattice sites . Frenkel defects occurs when cation leaves its lattice site and fits into an interstitial space. The neutrality of the crystal is being maintained and we considered all losses from interstitial positions.
which defect decrease density of the crystal ?
View SolutionWhich stoichiometric defect in crystals increses the density a solid?
View SolutionWhich point defect lowers the density of a crystal?
View SolutionWhat is the effect of Schottky defect on the density of crystal ?
View SolutionExamine the illustration of a portion of the deffective crystal and answer the following question :
(a) What are these type of vacancy defects called ?
(b) How is the density of a crystal affected by these defects ?
(c) Name one ionic compound which can show this type of defect in the crystalline state.
(d) How is the stoichiometry of the compound affected ?
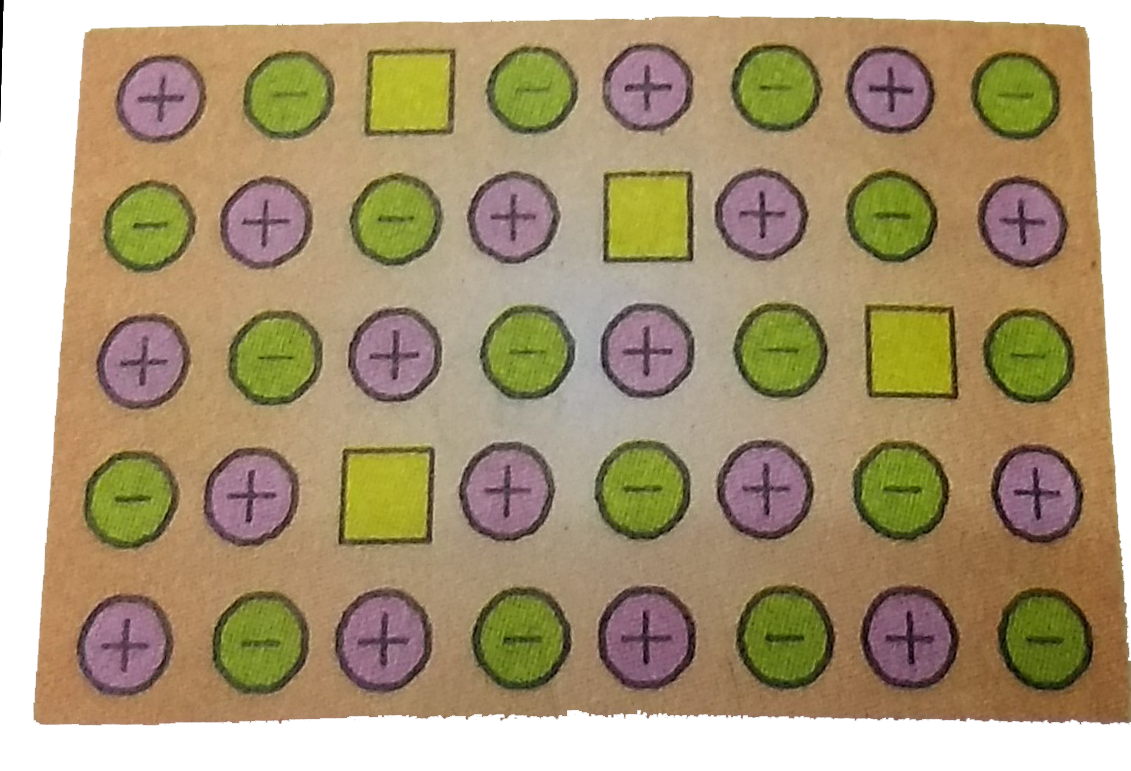
View SolutionWhich of the following defects, if present, lowers the density of the crystal ?
View SolutionExamine the defective crystal given below and answer the question that follows :

State if the above defect is stoichiometric or non-stoichiometric. How does this defect affect the density of the crystal ? Also, write the term used for this type of defect.
View SolutionDefects which do not disturb the stoichiometry are called stochiometric defect. At the time of crystal formation an ion may not occupy its expected position leaving a void or hole at that site. As a metter of fact one positive and one negative ion are missing from their respective positions leaving behind a pair of holes. This vacancy is a Schottky defect. Due to this defect density decreases. Defect arises in which certain atoms or ions have migrated to interstitial position some distance removed from the holes which they vacated. In this case there is no change in the density of the crystal.
In stoichiometric defects, the ratio of positive and negative ions as indicated by chemical formula of the compound
View Solution
