Arrange the following orbital in the increasing order of the energy
3s,4d,2p,4s,3p
To arrange the orbitals 3s,4d,2p,4s,3p in increasing order of energy, we will use the n + l rule. This rule states that the energy of an orbital can be determined by the sum of its principal quantum number (n) and its azimuthal quantum number (l). The lower the value of n + l, the lower the energy of the orbital. If two orbitals have the same n + l value, the one with the lower n value has lower energy.
1. Identify n and l for each orbital:
- For 3s:
- n = 3, l = 0 (s orbital)
- n + l = 3 + 0 = 3
- For 4d:
- n = 4, l = 2 (d orbital)
- n + l = 4 + 2 = 6
- For 2p:
- n = 2, l = 1 (p orbital)
- n + l = 2 + 1 = 3
- For 4s:
- n = 4, l = 0 (s orbital)
- n + l = 4 + 0 = 4
- For 3p:
- n = 3, l = 1 (p orbital)
- n + l = 3 + 1 = 4
2. List the n + l values:
- 3s: n + l = 3
- 4d: n + l = 6
- 2p: n + l = 3
- 4s: n + l = 4
- 3p: n + l = 4
3. Compare the n + l values:
- The lowest n + l value is 3 (for both 3s and 2p).
- The next lowest is 4 (for both 4s and 3p).
- The highest is 6 (for 4d).
4. Determine the order based on n + l values:
- Since 3s and 2p both have n + l = 3, we compare their n values:
- 2p (n = 2) has lower energy than 3s (n = 3).
- For 4s and 3p, both have n + l = 4, so we compare their n values:
- 3p (n = 3) has lower energy than 4s (n = 4).
5. Final order of increasing energy:
- 2p<3s<3p<4s<4d
Final Answer:
The increasing order of energy for the orbitals is:
2p<3s<3p<4s<4d
- For 3s:
- n = 3, l = 0 (s orbital)
- n + l = 3 + 0 = 3
- For 4d:
- n = 4, l = 2 (d orbital)
- n + l = 4 + 2 = 6
- For 2p:
- n = 2, l = 1 (p orbital)
- n + l = 2 + 1 = 3
- For 4s:
- n = 4, l = 0 (s orbital)
- n + l = 4 + 0 = 4
- For 3p:
- n = 3, l = 1 (p orbital)
- n + l = 3 + 1 = 4
- 3s: n + l = 3
- 4d: n + l = 6
- 2p: n + l = 3
- 4s: n + l = 4
- 3p: n + l = 4
- The lowest n + l value is 3 (for both 3s and 2p).
- The next lowest is 4 (for both 4s and 3p).
- The highest is 6 (for 4d).
- Since 3s and 2p both have n + l = 3, we compare their n values:
- 2p (n = 2) has lower energy than 3s (n = 3).
- For 4s and 3p, both have n + l = 4, so we compare their n values:
- 3p (n = 3) has lower energy than 4s (n = 4).
- 2p<3s<3p<4s<4d
The increasing order of energy for the orbitals is:
2p<3s<3p<4s<4d
Similar Questions
The arrangement of orbitals on the basis of energy is based upon their (n+l) value. Lower the value of (n+l), lower is the energy . For orbitals having same values of (n+l). The orbital with lower value of n will have lower energy.
I. Based upon the above information arrange the following orbitals in the increasing order of energy.
(a) 1s,2s,3s,2p (b) 4s,3s,3p,4d
(c) 2p,4d,5d,4f,6s (d) 5f,6d,7s,7p
II. Based upon the above information Solve the question. give below.
(a) which of the following orbitals has the lowest energy
4d,4f,5s,5p
(b) which of the following orbitals has the highest energy?
5p,5d,5f,6s,6pView SolutionArrange the following orbitals of H-atom in the increasing order of their energy.
3px,2s,4dxy,3s,4pz,3py,4sView SolutionWrite the increasing order of energies of 4s,3p,4p and 3d.
View SolutionArrange the following electrolytes in the increasing order of coagulation power for the coagulation of As2S3 sol :
K2SO4 CaCl2 Na3PO4 AlCl3View SolutionArrange with explanation the following ions in the increasing order of their sizes.
Cl−,N3−,O2−,S2−,Al3+View SolutionArrange the following in order of increasing energy for hydrogen atom 1s 2s 2p 3s 3p 3d 4s 4p
View SolutionThe decreasing order of energy of the 3d,4s,3p,3s orbital is :-
View SolutionP, Q R and S four places in the world as given in the following map. Arrange these places in increasing order of their biodiversity.
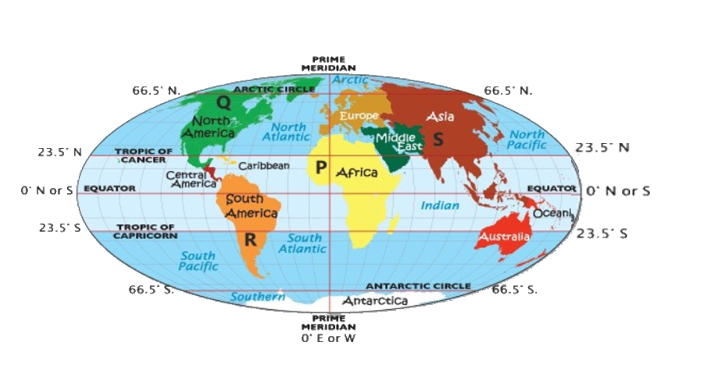 View Solution
View SolutionIn which of the following orbitals , the sum of (n+l) value is lowest ?
4s,3d,4pView SolutionIn which of the following orbitals , the sum of (n+l) value is lowest ?
4s,3d,4pView Solution

