The total number of orbitals in a shell having principal quantum n is
2n
n2
2n2
n+1
The correct Answer is:2
To determine the total number of orbitals in a shell with a principal quantum number n, we can follow these steps:
1. Understand Principal Quantum Number n:
- The principal quantum number n indicates the shell level of an electron in an atom. It can take positive integer values (1, 2, 3, ...).
2. Identify Azimuthal Quantum Number l:
- The azimuthal quantum number l defines the subshells within a shell and can take values from 0 to n−1.
- For each value of l:
- l=0 corresponds to the s-subshell.
- l=1 corresponds to the p-subshell.
- l=2 corresponds to the d-subshell.
- l=3 corresponds to the f-subshell, and so on.
3. Count Orbitals in Each Subshell:
- Each subshell has a specific number of orbitals:
- s-subshell (l=0): 1 orbital
- p-subshell (l=1): 3 orbitals
- d-subshell (l=2): 5 orbitals
- f-subshell (l=3): 7 orbitals
- The number of orbitals in a subshell is given by the formula 2l+1.
4. Calculate Total Number of Orbitals:
- For a given principal quantum number n, the total number of orbitals can be calculated by summing the number of orbitals in all subshells from l=0 to l=n−1.
- This can be expressed mathematically as:
Total orbitals=n−1∑l=0(2l+1)
- This simplifies to n2 because:
- For n=1: 12=1
- For n=2: 22=4
- For n=3: 32=9
- And so on...
5. Conclusion:
- Therefore, the total number of orbitals in a shell with principal quantum number n is n2.
Final Answer:
The total number of orbitals in a shell having principal quantum number n is n2.
---
- The principal quantum number n indicates the shell level of an electron in an atom. It can take positive integer values (1, 2, 3, ...).
- The azimuthal quantum number l defines the subshells within a shell and can take values from 0 to n−1.
- For each value of l:
- l=0 corresponds to the s-subshell.
- l=1 corresponds to the p-subshell.
- l=2 corresponds to the d-subshell.
- l=3 corresponds to the f-subshell, and so on.
- Each subshell has a specific number of orbitals:
- s-subshell (l=0): 1 orbital
- p-subshell (l=1): 3 orbitals
- d-subshell (l=2): 5 orbitals
- f-subshell (l=3): 7 orbitals
- The number of orbitals in a subshell is given by the formula 2l+1.
- For a given principal quantum number n, the total number of orbitals can be calculated by summing the number of orbitals in all subshells from l=0 to l=n−1.
- This can be expressed mathematically as:
Total orbitals=n−1∑l=0(2l+1)
- This simplifies to n2 because:
- For n=1: 12=1
- For n=2: 22=4
- For n=3: 32=9
- And so on...
- Therefore, the total number of orbitals in a shell with principal quantum number n is n2.
The total number of orbitals in a shell having principal quantum number n is n2.
Topper's Solved these Questions
- STRUCTURE OF ATOM BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - ASSIGNMENT ( SECTION -C) Objective Type Questions (More than one options are correct)
15 Videos
- STRUCTURE OF ATOM BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - ASSIGNMENT ( SECTION -D) Linked Comprehension Type Questions)
9 Videos
- STRUCTURE OF ATOM BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - ASSIGNMENT ( SECTION -A) Objective Type Questions (One option is correct)
47 Videos
- STRUCTURE OF ATOMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - ASSIGNMENT (SECTION -D) Assertion-Reason Type Questions
15 Videos
- SURFACE CHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SURFACE CHEMISTRY EXERCISE - Assignment Section - C (Assertion - Reason type questions)
10 Videos
Similar Questions
Knowledge Check
Assertion : The maximum number of electrons in the shell with principle quantum number n is equal to 2n2.
Reason : Two electrons can have the same value of three quantum numbers n, l and ml, but must have the opposite spin quantum number.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
The number of orbitals in a quantum shell is equal to ……………..
View SolutionThe number of orbitals in the quantum level n = 4 is
View SolutionThe maximum number of electrons can have principal quantum number n=3 and spin quantum number ms=1/2 is
View SolutionThe shape of orbitals are related to the ratio of principal quantum number (n) to substiary quantum number (k,a modifacation of Bohr-sommerfield theory ).The value of k for any shell has a value ranging betwe3en n to l .The amximum value for k is given for x sub-shell white k becomes with p, d,f........ repectively upto minimum value
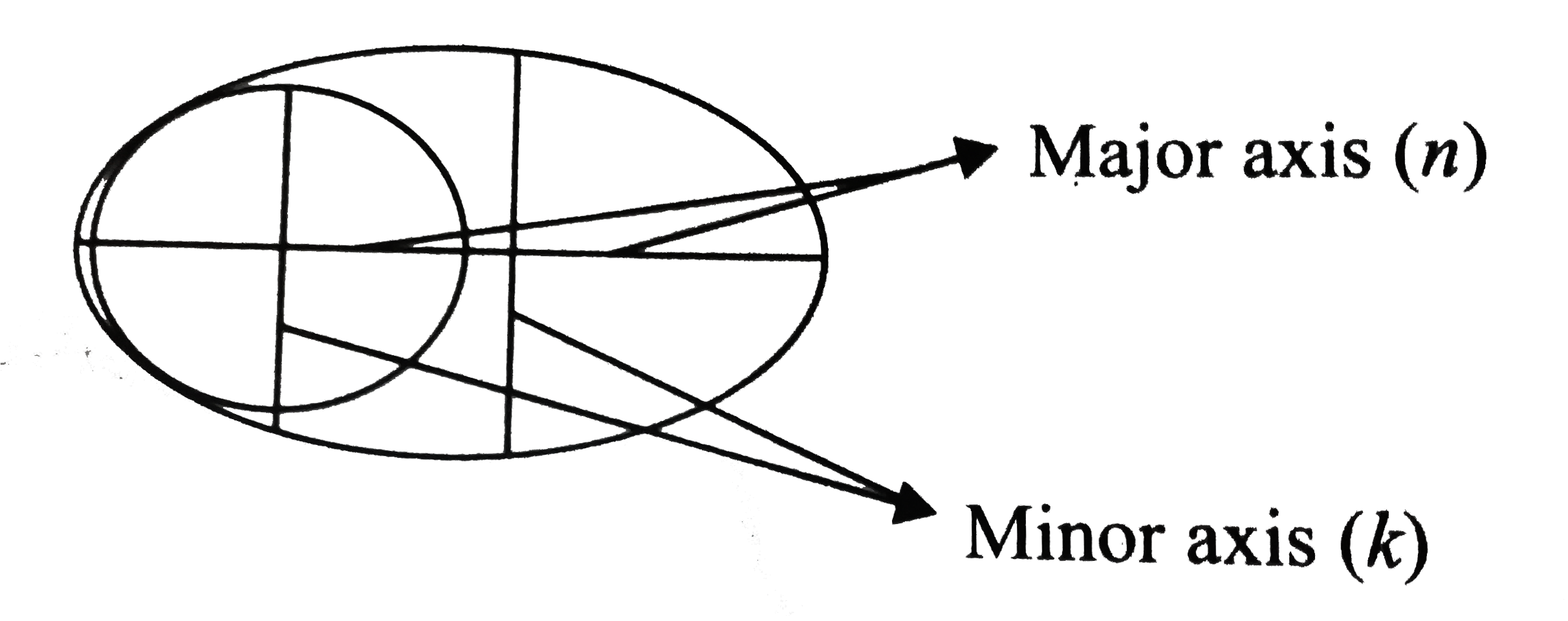
If n is the major axis and k is th e minor axis , then n/k=1 for circular shape white n/k>1 for elliptical shape
Which is correct according to the increasing elliptical number of sub-shell ?
View SolutionThe shape of orbitals are related to the ratio of principal quantum number (n) to substiary quantum number (k,a modifacation of Bohr-sommerfield theory ).The value of k for any shell has a value ranging betwe3en n to l .The amximum value for k is given for x sub-shell white k becomes with p, d,f........ repectively upto minimum value
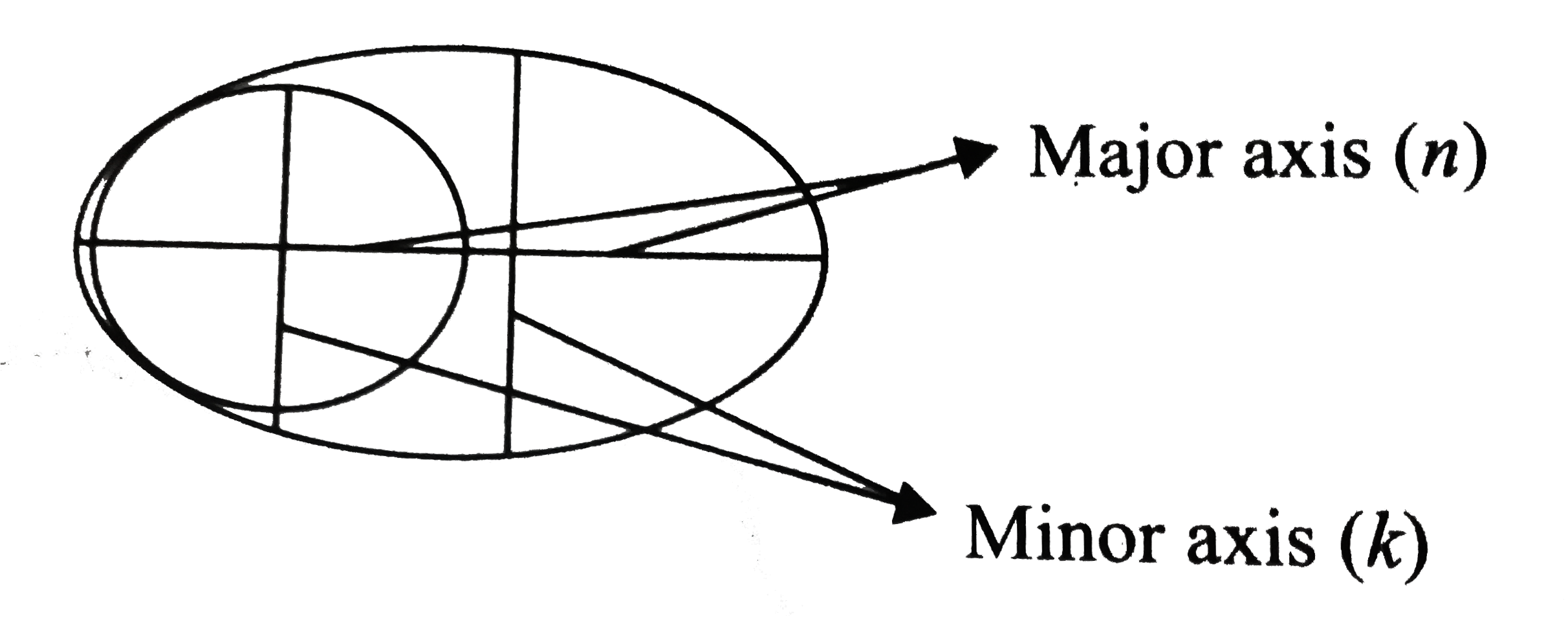
If n is the major axis and k is th e minor axis , then n/k=1 for circular shape white n/k>1 for elliptical shape
Which orbit shape has highest n/k>>1 value?
View SolutionThe shape of orbitals are related to the ratio of principal quantum number (n) to substiary quantum number (k,a modifacation of Bohr-sommerfield theory ).The value of k for any shell has a value ranging betwe3en n to l .The amximum value for k is given for x sub-shell white k becomes with p, d,f........ repectively upto minimum value
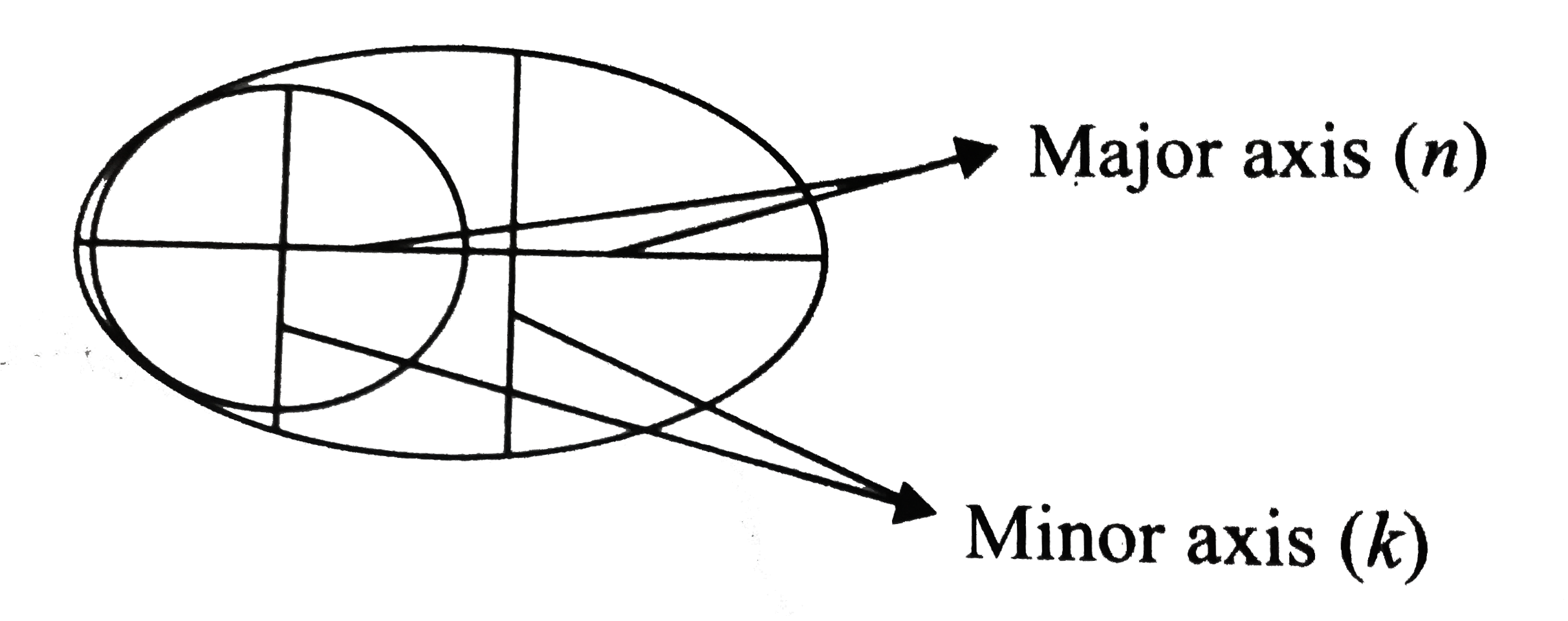
If n is the major axis and k is th e minor axis , then n/k=1 for circular shape white n/k>1 for elliptical shape
Which shape is used to be circular having n/k value
View SolutionThe shape of orbitals are related to the ratio of principal quantum number (n) to substiary quantum number (k,a modifacation of Bohr-sommerfield theory ).The value of k for any shell has a value ranging betwe3en n to l .The amximum value for k is given for x sub-shell white k becomes with p, d,f........ repectively upto minimum value
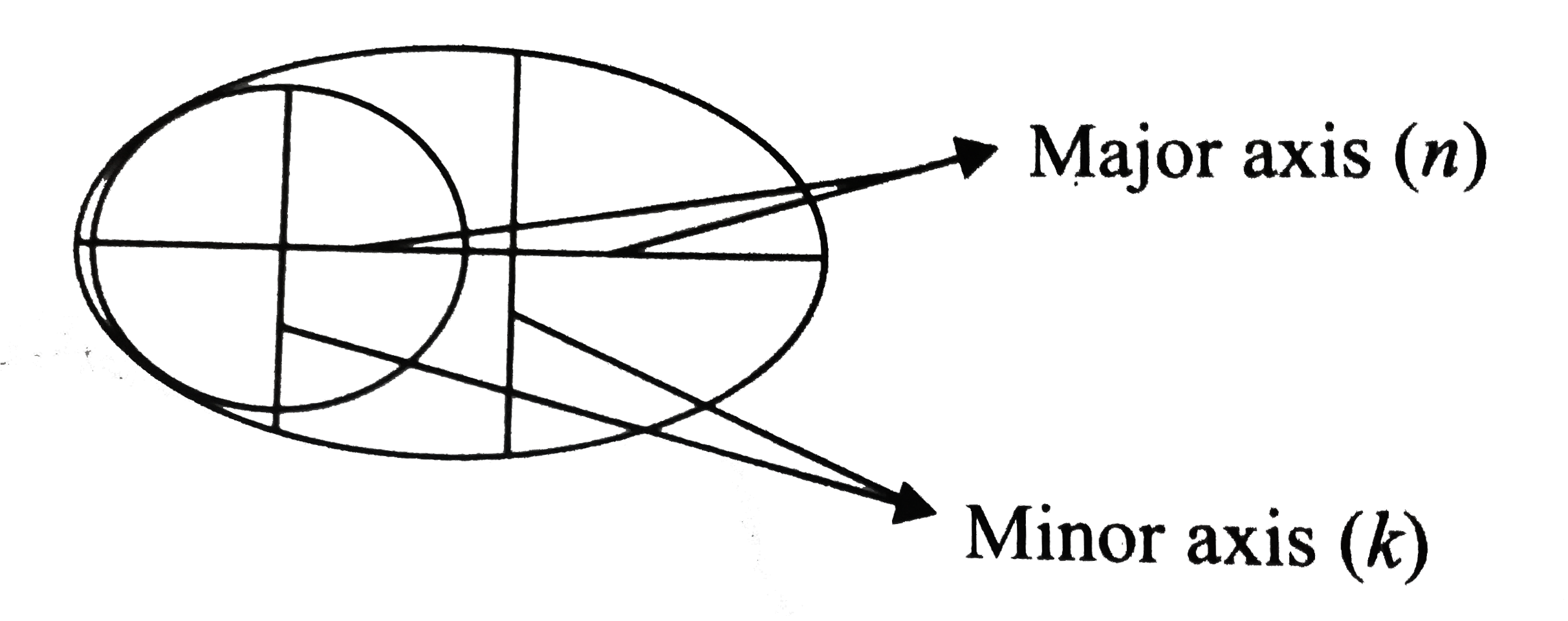
If n is the major axis and k is th e minor axis , then n/k=1 for circular shape white n/k>1 for elliptical shape
Which value of n and k suggest about the shape of 3s orbitsl?
View Solution
