The half cell potentials of a halfcell A(x+n)+,Ax+∣pt were found to be as follows : %of reduced form24.448.8Half cell potential (V)0.1010.115
Determinwe the value of n.
The correct Answer is:B
To determine the value of n in the given half-cell potentials, we can follow these steps:
Step 1: Understand the Reduction Reactions
The reduction reactions for the half-cells can be represented as follows:
- For A(x+n)+:
A(x+n)++ne−→Ax
- For A(x)+:
A(x)++e−→Ax
Step 2: Identify the Given Data
From the problem statement, we have:
- Percentage of reduced form:
- A(x+n)+: 24.4%
- A(x)+: 48.8%
- Half-cell potentials:
- E(A(x+n)+)=0.101V
- E(A(x)+)=0.115V
Step 3: Calculate the Concentrations
Using the percentage of reduced forms, we can determine the concentrations of the oxidized and reduced forms:
- For A(x+n)+:
- Reduced form concentration = 24.4
- Oxidized form concentration = 100−24.4=75.6
- For A(x)+:
- Reduced form concentration = 48.8
- Oxidized form concentration = 100−48.8=51.2
Step 4: Apply the Nernst Equation
The Nernst equation is given by:
E=E0+0.059nlog((Products)(Reactants))
For the first half-cell:
0.101=E0+0.059nlog(75.624.4)(1)
For the second half-cell:
0.115=E0+0.059nlog(51.248.8)(2)
Step 5: Subtract Equation (1) from Equation (2)
Subtracting equation (1) from equation (2):
0.115−0.101=0.059n(log(51.248.8)−log(75.624.4))
0.014=0.059n(log(51.248.8)−log(75.624.4))
Step 6: Calculate the Logarithmic Values
Calculate the logarithmic values:
- log(51.248.8)
- log(75.624.4)
Let's compute these:
1. 51.248.8≈1.048 → log(1.048)≈0.020
2. 75.624.4≈3.1 → log(3.1)≈0.491
Step 7: Substitute Back into the Equation
Substituting the logarithmic values back into the equation:
0.014=0.059n(0.020−0.491)
0.014=0.059n(−0.471)
Step 8: Solve for n
Rearranging gives:
n=0.059⋅(−0.471)0.014
Calculating this yields:
n≈2
Final Answer
The value of n is approximately 2.
---
The reduction reactions for the half-cells can be represented as follows:
- For A(x+n)+:
A(x+n)++ne−→Ax
- For A(x)+:
A(x)++e−→Ax
From the problem statement, we have:
- Percentage of reduced form:
- A(x+n)+: 24.4%
- A(x)+: 48.8%
- Half-cell potentials:
- E(A(x+n)+)=0.101V
- E(A(x)+)=0.115V
Using the percentage of reduced forms, we can determine the concentrations of the oxidized and reduced forms:
- For A(x+n)+:
- Reduced form concentration = 24.4
- Oxidized form concentration = 100−24.4=75.6
- Reduced form concentration = 48.8
- Oxidized form concentration = 100−48.8=51.2
The Nernst equation is given by:
E=E0+0.059nlog((Products)(Reactants))
0.101=E0+0.059nlog(75.624.4)(1)
0.115=E0+0.059nlog(51.248.8)(2)
Subtracting equation (1) from equation (2):
0.115−0.101=0.059n(log(51.248.8)−log(75.624.4))
0.014=0.059n(log(51.248.8)−log(75.624.4))
Calculate the logarithmic values:
- log(51.248.8)
- log(75.624.4)
1. 51.248.8≈1.048 → log(1.048)≈0.020
2. 75.624.4≈3.1 → log(3.1)≈0.491
Substituting the logarithmic values back into the equation:
0.014=0.059n(0.020−0.491)
0.014=0.059n(−0.471)
Rearranging gives:
n=0.059⋅(−0.471)0.014
Calculating this yields:
n≈2
The value of n is approximately 2.
Topper's Solved these Questions
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION - H) (Multiple True-False Type Question)
3 Videos
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION - I) (Subjective Type Question)
12 Videos
- ELECTROCHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROCHEMISTRY EXERCISE - Assignment (SECTION - F) Matrix-Match Type Questions
4 Videos
- COORDINATION COMPOUNDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COORDINATION COMPOUNDS EXERCISE - Assignment (Section-J Aakash Challenger Questions )
10 Videos
- ENVIRONMENTAL CHEMISTRYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ENVIRONMENTAL CHEMISTRYEXERCISE - ASSIGNMENT (SECTION-D) (Assertion - Reason Type Questions)
4 Videos
Similar Questions
The half cell potential of a half-cell Ax+,A(x+n)+∣Pt were found to be as follows:
%of reduced form24.448.8Cell potential/N0.1010.115
Determine the value of n.
[take 2.303RTF=0.05,log1024.4=1.387,log1075.6=1.878log1048.8=1.688,log1051.2=1.709]
View SolutionThe standard reduction potential for the half cell :
NOc−3(aq)+2Hc−+e−→NO2(g)+H2O is 0.78V.
Calculate the reduction potential in 8MH⊕.
View SolutionThe standard reduction potential for the half cell :
NOc−3(aq)+2Hc−+e−→NO2(g)+H2O is 0.78V.
a. Calculate the reduction potential in 8MH⊕.
b. What will be the reduction potential of the half cell in a neutral solution ? Assume all the other species to be at unit concentration.
View SolutionThe standard electrode potentials of the two half cells are given below: Ni2++2e→Ni(s),Eo=−0.25V,Zn2++2e→Zn(s),Eo=−0.77V. The voltage of the final cell formed by combining the two half cells would be:
View Solutionwhen two half-cells of electrode potential of E1 and E2 are combined to form a half cell of electrode potential E3 , then
(when n1,n2andn3 are no. of electrons exchanged in first second and combined half-cells:
View SolutionFor a hypothetical reaction X→Y, the value of rate constant is 0.75sec−1. If the concentration of X is reduced to half, then value of the constant is
View Solution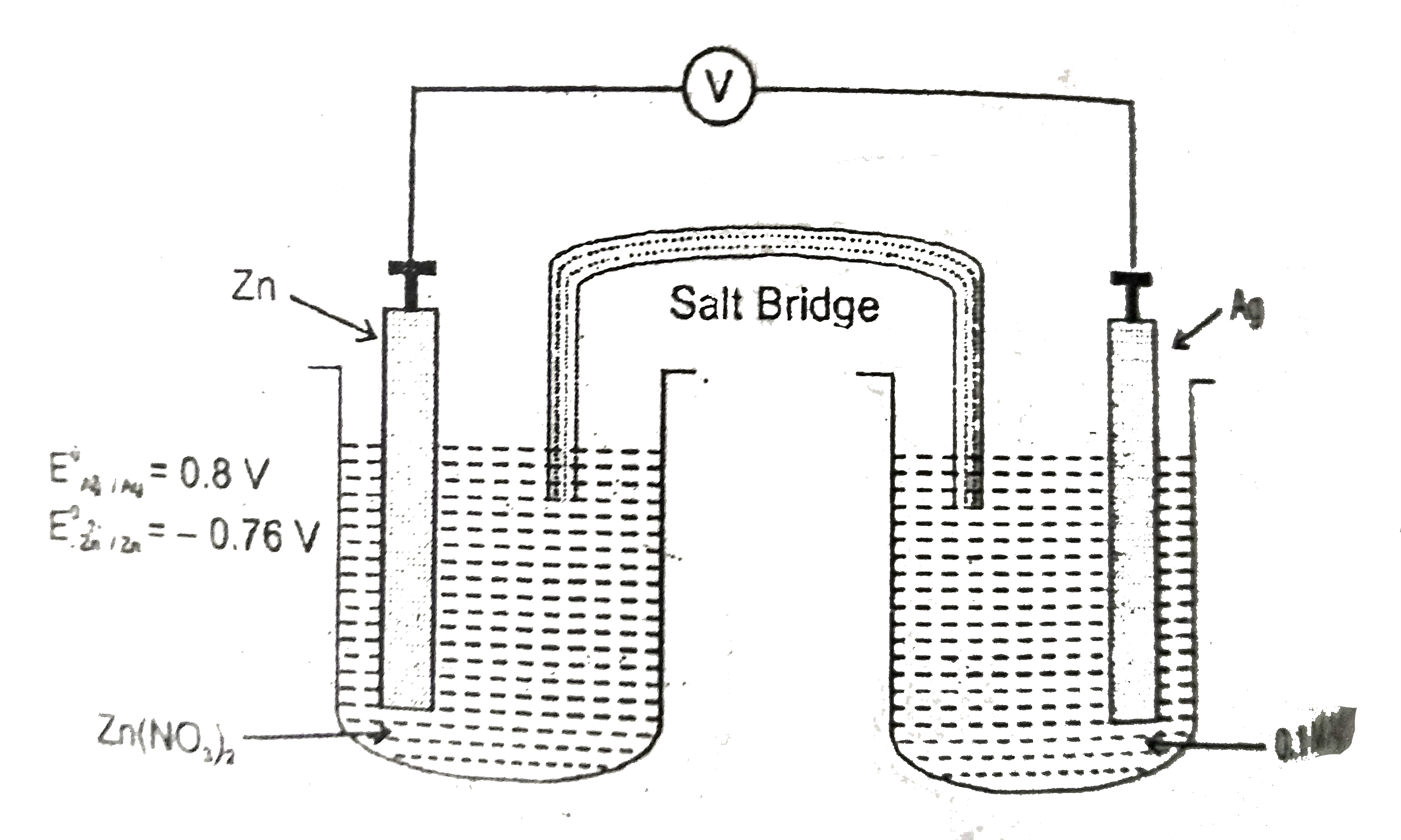
Consider the following electrochemical cell.
(a). Write a balanced net ionic equation for the spontaneous reaction that take place in the cell.
(b). Calculate the standard cell potential E0 for the cell reaction.
(c). If the cell emf is 1.6V what is the concentration of Zn2+?
(d). How will the cell potential be affected if Kl is added to Ag+ half-cell?
View SolutionThe potential of the cell Cu,Cu2+(0.1M)//HCl(xM),Cl2,Ptis 1.07 V. If the standard potential of copper and chlorine electrodes are 0.34 V and 1.36 V, calculate the concentration of HCI.
View SolutionComponents of water potential of four cells of an acitvely transpiring monocot plant are
cellosmotic Potenial Pressure Potentiala−0.90.5b−0.80.6c−0.60.1d−0.70.4
Identify the four cells as root hair, Cortical cell, endodermal and pericycle cells
View SolutionTwo half cells have reduction potentials −0.76V and −0.13V respectively . A galvanic cell is made from these two half cells . Which of the following statements is correct ?
View Solution
